
§5设备更新问题 种设备(例如汽车、机床等)在使用过程中总会变旧,以至 于损坏,通常,或者对旧设备进行维修,或者卖掉旧设备再买新的 (更新)。在给定的年限年内,使用该设备进行生产,设备应使 用多少年后再进行更新,以使得年内总的纯收入最大,这就是设 备更新问题。一般说来,一种设备使用时间过长,由于收入减少, 维修费用增大,所以从经济上看并不合算。但是,使用时间过短, 频繁更换设备也是不合算的,这类问题存在一个最佳的更新周期。 在讨论设备的最佳更新周期问题时,一般要考虑下面几个因素: 1°「k)一在第k年机龄为的一台设备运转一年带来的收入额。 显然,是的递减函数,这是因为设备随着使用时间的增加(即 机龄的增长)而变旧,因而收入减少。 2°O)一在第k年机龄为的一台设备所需的维修费。O)是的 递增函数,这是因为随着使用年限的增加,设备变旧,维修费用也 逐渐增加。 3°C①一在第k年卖掉旧设备购买新设备所需款项。Ck是的 递增函数,因为随着设备的老化,旧设备越不值钱,卖旧买新所需 的款项越大
§5 设备更新问题 • 一种设备(例如汽车、机床等)在使用过程中总会变旧,以至 于损坏,通常,或者对旧设备进行维修,或者卖掉旧设备再买新的 (更新)。在给定的年限n年内,使用该设备进行生产,设备应使 用多少年后再进行更新,以使得n年内总的纯收入最大,这就是设 备更新问题。一般说来,一种设备使用时间过长,由于收入减少, 维修费用增大,所以从经济上看并不合算。但是,使用时间过短, 频繁更换设备也是不合算的,这类问题存在一个最佳的更新周期。 • 在讨论设备的最佳更新周期问题时,一般要考虑下面几个因素: • 1°r k (t)—在第k年机龄为t的一台设备运转一年带来的收入额。 显然, r k (t)是t的递减函数,这是因为设备随着使用时间的增加(即 机龄的增长)而变旧,因而收入减少。 • 2°Ok (t)—在第k年机龄为t的一台设备所需的维修费。 Ok (t)是t的 递增函数,这是因为随着使用年限的增加,设备变旧,维修费用也 逐渐增加。 • 3°Ck (t) —在第k年卖掉旧设备购买新设备所需款项。 Ck (t) 是t的 递增函数,因为随着设备的老化,旧设备越不值钱,卖旧买新所需 的款项越大
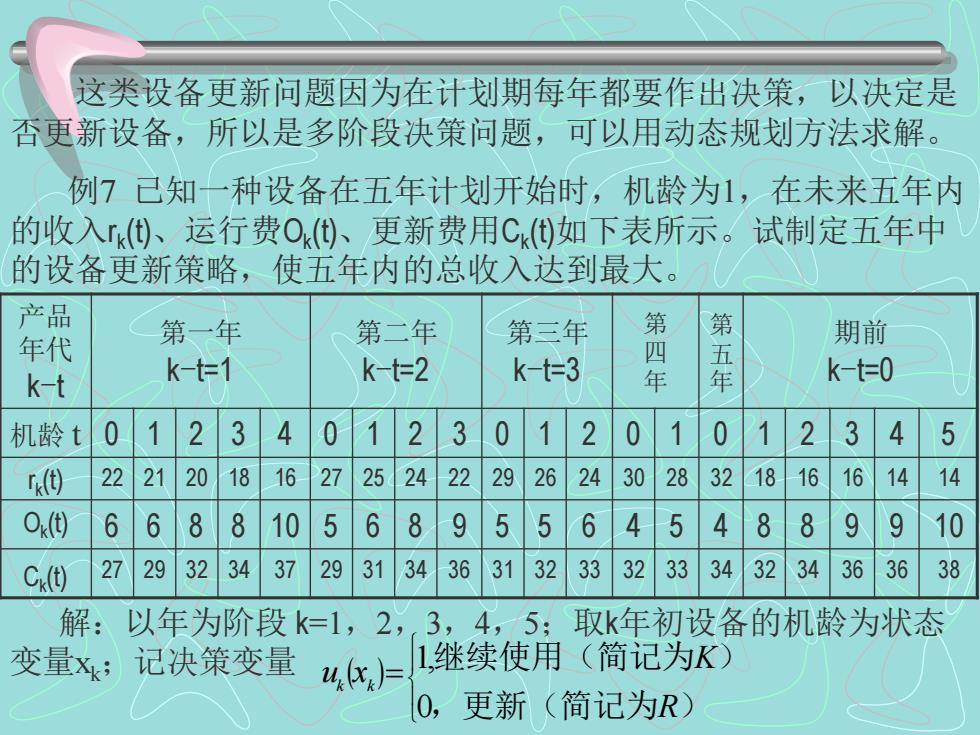
这类设备更新问题因为在计划期每年都要作出决策,以决定是 否更新设备,所以是多阶段决策问题,可以用动态规划方法求解。 例7已知一种设备在五年计划开始时,机龄为1,在未来五年内 的收入k)、运行费Ok()、更新费用C)如下表所示。试制定五年中 的设备更新策略,使五年内的总收入达到最大。 产品 年代 第一年 第二年 第三年 期前 k-t k-t=1 k-t=2 k-t=3 四年 五年 k-t=0 机龄t 0 2 3 4 0 1 2 3 0 1 2 0 1 0 1 2 3 4 5 因 22 21 20 18 16 27 25 24 22 29 26 24 30 28 32 18 16 16 14 14 .(t) 6 68 8 10 5 6 8 9 5 5 6 4 5 4 8 8 9 9 10 C(t) 2729 32 34 37 29 31 34 36 31 32 33 32 33 34 32 34 36 36 38 解:以年为阶段k=1,2,3, 4,5: 取k年初设备的机龄为状态 变量X: 记决策变量 1继续使用(简记为K) O,更新(简记为R)
这类设备更新问题因为在计划期每年都要作出决策,以决定是 否更新设备,所以是多阶段决策问题,可以用动态规划方法求解。 例7 已知一种设备在五年计划开始时,机龄为1,在未来五年内 的收入r k (t)、运行费Ok (t)、更新费用Ck (t)如下表所示。试制定五年中 的设备更新策略,使五年内的总收入达到最大。 产品 年代 k-t 第一年 k-t=1 第二年 k-t=2 第三年 k-t=3 第 四 年 第 五 年 期前 k-t=0 机龄 t 0 1 2 3 4 0 1 2 3 0 1 2 0 1 0 1 2 3 4 5 r k (t) 22 21 20 18 16 27 25 24 22 29 26 24 30 28 32 18 16 16 14 14 Ok (t) 6 6 8 8 10 5 6 8 9 5 5 6 4 5 4 8 8 9 9 10 Ck (t) 27 29 32 34 37 29 31 34 36 31 32 33 32 33 34 32 34 36 36 38 解:以年为阶段 k=1,2,3,4,5;取k年初设备的机龄为状态 变量xk;记决策变量 ( ) = ,更新(简记为 ) 继续使用(简记为 ) R K u xk k 0 1

则 +1, 4,x=1 Xk+ 4c=0 记人(x)为第k年到第5年底的最大总收入, 则动态规划基本 方程是: f(x)=max K:(x)-O(x)+f4(x) R:n(0)-(0)-C()+f(1) 6(x6)=0 k=5,4,3,2,1 k=5 85=1,2,3,4,5 K:)-O,(1)+f(2) f;(1)=max R:rO)-O,(0)-C,()+f) K:28-5 23 max =max =23 u5(1)=1 R:32-4-33 K:r(2)-O,(2)+f(3) f;(2)=max R:r:0)-O,0)-C,(2)+f) K:24-6 18 max max R:32-4-33 5 =18 u5(2)=1
则 ( ) ( ) = + = + = 1, 0 1, 1 1 k k k k k k u x x u x x 记fk(xk)为第k年到第5年底的最大总收入,则动态规划基本 方程是: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) − − + − + = + + + : 0 0 1 : max 1 1 1 k k k k k k k k k k k k k R r O C x f K r x O x f x f x f6(x6)=0 k=5,4,3,2,1 k=5 x5 =1,2,3,4,5 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − = − − − = − − + − + = 23 5 23 max : 32 4 33 : 28 5 max : 0 0 1 1 : 1 1 2 1 max 5 5 5 6 5 5 6 5 R K R r O C f K r O f f u5(1)=1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − = − − − = − − + − + = 18 5 18 max : 32 4 33 : 24 6 max : 0 0 2 1 : 2 2 3 2 max 5 5 5 6 5 5 6 5 R K R r O C f K r O f f u5(2)=1

K:r(3)-O,(3)+f,(4) f (3)=max R:50)-O,(0)-C,3)+f) K:22-9 13 =max =max R:32-4-36 -8 =13 u5(3)=1 K:r(4)O,(4)+f(⑤) f(4)=max R:r0)-O,(0)-C,(4)+f,) K:16-10 6 max R:32-4-37 =max _9 =6 u5(4)=1 K:r(⑤)-O,(⑤)+f(6) f;(5)=max R:r,(0)-O,(O)-C,(⑤)+f() K:14-10 4 max max 4 u5(5)= R:32-4-38 -10
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − = − − − = − − + − + = 13 8 13 max : 32 4 36 : 22 9 max : 0 0 3 1 : 3 3 4 3 max 5 5 5 6 5 5 6 5 R K R r O C f K r O f f u5(3)=1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − = − − − = − − + − + = 6 9 6 max : 32 4 37 :16 10 max : 0 0 4 1 : 4 4 5 4 max 5 5 5 6 5 5 6 5 R K R r O C f K r O f f u5(4)=1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − = − − − = − − + − + = 4 10 4 max : 32 4 38 :14 10 max : 0 0 5 1 : 5 5 6 5 max 5 5 5 6 5 5 6 5 R K R r O C f K r O f f u5(5)=1

k=4 X4=1,2,3,4 f,(①)=max K,)-O+f52) R:0)-O,(0)-C4()+f(①) K:26-5+18 39 =max =39 u4(1)=1 R:30-4-32+23 max f (2)=max K:r(2)-O,(2)+f3) R:r(0)O.(0)-C4(2)+f,) K:24-8+13 29 max max =29 u4(2)=1 R:30-4-34+23 15 K:r(3)-O.(3)+f(4) f(3)= max R:r0)-O,0)-C,(3)+f() K:18-8+6 16 =max =max =16 u4(3)=1 R:30-4-34+23 15 f(4)= K:r4)-O,(4)+f,(⑤) max R:r(0)-O(0)-C(4)+f,(1) K:14-9+4 9 =max =max =13 u4(4)=0 R:30-4-36+23 13
k=4 x4=1,2,3,4 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 39 17 39 max : 30 4 32 23 : 26 5 18 max : 0 0 1 1 : 1 1 2 1 max 4 4 4 5 4 4 5 4 R K R r O C f K r O f f u4(1)=1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 29 15 29 max : 30 4 34 23 : 24 8 13 max : 0 0 2 1 : 2 2 3 2 max 4 4 4 5 4 4 5 4 R K R r O C f K r O f f u4(2)=1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 16 15 16 max : 30 4 34 23 :18 8 6 max : 0 0 3 1 : 3 3 4 3 max 4 4 4 5 4 4 5 4 R K R r O C f K r O f f ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 13 13 9 max : 30 4 36 23 :14 9 4 max : 0 0 4 1 : 4 4 5 4 max 4 4 4 5 4 4 5 4 R K R r O C f K r O f f u4(4)=0 u4(3)=1

k=3 X3=1,2,3 K:r5(0)-O,()+f4(2) (1)=max R:r(O)-O,(0)-C,①+f() K:25-6+29 48 max max =48 32 u3(1)=1 R:29-5-31+39 K:5(2)-O,(2)+f(3) (2)= max R:50)-O,(0)-C,(2)+f(I) K:20-8+16 28 max =max 31 R:29-5-32+39 31 山3(2)=0 K:5(3)-O,(3)+f(4) f;(3)=max R:50)-O,)-C,(3)+f() K:16-9+13 20 max max R:29-5-36+39 27 =27 山3(3)=0
k=3 x3=1,2,3 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 48 32 48 max : 29 5 31 39 : 25 6 29 max : 0 0 1 1 : 1 1 2 1 max 3 3 3 4 3 3 4 3 R K R r O C f K r O f f u3(1)=1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 31 31 28 max : 29 5 32 39 : 20 8 16 max : 0 0 2 1 : 2 2 3 2 max 3 3 3 4 3 3 4 3 R K R r O C f K r O f f u3(2)=0 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 27 27 20 max : 29 5 36 39 :16 9 13 max : 0 0 3 1 : 3 3 4 3 max 3 3 3 4 3 3 4 3 R K R r O C f K r O f f u3(3)=0

k=2X2=1,2 K:r⑩-O,(①+f(2) f,(1)=max R:5(0)-O,0)-C,(四)+f1) K:21-6+31 46 =max max =46 (1)=1 R:27-5-29+48 41 K:5(2)O,(2)+f(3) f;(2)=max R:5(0)-O,(0)-C,(2)+f3() K:16-8+27 35 max =max 3636 2(2) =0 R:27-5-34+48 k=1 X=1 K:r@)-O,(0)+f(2) f (1)=max R:r(0)-O,(0)-C,)+fI) K:18-8+36 46 max max 46 1(1)=1 R:22-6-32+46 30 至此,根据计算过程反推回去, 可得最优更新策略如下:u,(1 =1,K;山2(2)=0,R;u3(1)=1;u山4(2)=1;u5(3)=1,K
k=2 x2=1,2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 46 41 46 max : 27 5 29 48 : 21 6 31 max : 0 0 1 1 : 1 1 2 1 max 2 2 2 3 2 2 3 2 R K R r O C f K r O f f u2(1)=1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 36 36 35 max : 27 5 34 48 :16 8 27 max : 0 0 2 1 : 2 2 3 2 max 2 2 2 3 2 2 3 2 R K R r O C f K r O f f u2(2)=0 k=1 x1=1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = = − − + − + = − − + − + = 46 30 46 max : 22 6 32 46 :18 8 36 max : 0 0 1 1 : 1 1 2 1 max 1 1 1 2 1 1 2 1 R K R r O C f K r O f f u1(1)=1 至此,根据计算过程反推回去,可得最优更新策略如下:u1(1) =1,K;u2(2)=0,R;u3(1)=1;u4(2)=1;u5(3)=1,K