
§7排队象统的最优化问题 7.1排队系统的最优化问题 排队系统的最优化问题分为两类:系统设计最优化和系统控制最 优化。前者称为静态最优问题,从排队论一诞生起就成为人们研究 的内容,目的在于使系统达到最大效益,或者说在一定的质量指标 下使系统最为经济;后者称为动态最优问题,是指一个给定的系统, 如何运营可使某个目标函数达到最优,这是近年来排队论研究的重 点之一。我们这里只讨论静态最优问题。 了 在一般情况下,提高服务水平(数量、质量)可减少顾客的等 待费用(损失),但却常常增加了服务机构的成本。因此,最优化 的目标之一就是使两者的费用之和为最小,并确定达到这个目标的 最优服务水平。另一个常用的目标函数是使纯收入或利润(服务收 入与服务成本之差)为最大。如图10一11所示。 嘴 合并费用 服务费用 等待费用 图10-11 最小 服务水平
§7 排队系统的最优化问题 7.1 排队系统的最优化问题 排队系统的最优化问题分为两类:系统设计最优化和系统控制最 优化。前者称为静态最优问题,从排队论一诞生起就成为人们研究 的内容,目的在于使系统达到最大效益,或者说在一定的质量指标 下使系统最为经济;后者称为动态最优问题,是指一个给定的系统, 如何运营可使某个目标函数达到最优,这是近年来排队论研究的重 点之一。我们这里只讨论静态最优问题。 在一般情况下,提高服务水平(数量、质量)可减少顾客的等 待费用(损失),但却常常增加了服务机构的成本。因此,最优化 的目标之一就是使两者的费用之和为最小,并确定达到这个目标的 最优服务水平。另一个常用的目标函数是使纯收入或利润(服务收 入与服务成本之差)为最大。如图10-11所示。 图10-11 费 用 合并费用 服务费用 等待费用 最小 服务水平

假定在稳定状态下,各种费用都是按单位时间来考虑的。一般说 来,服务费用(成本)是可以确切计算的,而顾客的等待费用就有 许多不同情况,象机械故障问题中等待费用(由于机器待修而使生 产遭受的损失)是可以确切计算的,但象病人就诊的等待费用(由 于拖延治疗使病情恶化所受的损失),或由于队列过长而失掉潜在 顾客所造成的营业损失,就只能根据统计的经验资料来估计。 服务水平也可以由不同形式来表示,主要的是平均服务率 (代表服务机构的服务能力和经验等),其次是服务设备,如服务 台的个数C,以及由队列所占空间大小决定的队列最大限制数N等, 服务水平也可以通过服务强度来表示。 我们常用的求解方法:对于离散变量常用边际分析法,对于连 续变量常用经典的微分法
假定在稳定状态下,各种费用都是按单位时间来考虑的。一般说 来,服务费用(成本)是可以确切计算的,而顾客的等待费用就有 许多不同情况,象机械故障问题中等待费用(由于机器待修而使生 产遭受的损失)是可以确切计算的,但象病人就诊的等待费用(由 于拖延治疗使病情恶化所受的损失),或由于队列过长而失掉潜在 顾客所造成的营业损失,就只能根据统计的经验资料来估计。 服务水平也可以由不同形式来表示,主要的是平均服务率μ (代表服务机构的服务能力和经验等),其次是服务设备,如服务 台的个数C,以及由队列所占空间大小决定的队列最大限制数N等, 服务水平也可以通过服务强度ρ来表示。 我们常用的求解方法:对于离散变量常用边际分析法,对于连 续变量常用经典的微分法

72MWM/1模型中的最优服务率u (1)标准的M/M1模型 取目标函数Z为单位时间服务成本与顾客在系统逗留费用之和 的期望值:Z=Cu+cwLs 其中c为u=1时服务机构单位时间的服务费用,c,为每个顾客在系统 停留单位时间的费用。 将Ls的算式代入,有Z=cs+cwW(A) 为了求最小,令 da es-e d 解得最优服务率为: +2 根号前取正号,是为保证>A,p<1。 例8设货船按普阿松流到达某一港口,平均到达率=50(条/天), 平均卸货率为μ。又知船在港口停泊一天的费用为1货币单位,平均 卸货费为uCs,其中c=2货币单位,求使总费用最小的平均服务率。 解:将=50,cw=1,cs=2代入公式,得最优服务率 μ-50+55(条/大)
7.2 M/M/1模型中的最优服务率μ (1)标准的M/M/1模型 取目标函数Z为单位时间服务成本与顾客在系统逗留费用之和 的期望值: Z=cSμ+cwLs 其中cS为μ=1时服务机构单位时间的服务费用,cw为每个顾客在系统 停留单位时间的费用。 将Ls的算式代入,有 Z=cSμ+cw·λ/(μ-λ) 为了求最小,令 ( ) 0 μ λ λ μ 2= − =cS−cw d dZ 解得最优服务率为: μ λ λ S w c c = + 根号前取正号,是为保证μ>λ,ρ<1。 例8 设货船按普阿松流到达某一港口,平均到达率λ=50(条/天), 平均卸货率为μ。又知船在港口停泊一天的费用为1货币单位,平均 卸货费为μcS,其中cS =2货币单位,求使总费用最小的平均服务率。 解:将λ=50,cw=1, cS =2代入公式,得最优服务率 55 2 50 μ =50+ = (条/天)

(2)MMW/1/N/6o模型 在系统中顾客最大限制数为N的情沉下,如系统中已有N个顾客 则后来的顾客即被拒绝,被拒绝的概率为P~,而1-P即为能接受服务 的概率。 单位时间实际进入服务机构的平均顾客数为(1-P),在稳定状 态下,它也等于单位时间实际服务完的平均顾客数。设每服务1人能 收入G元,于是单位时间收入的期望值是A(1-P)G元。 纯利润:Z=(1-P)G-CsW 由公式PwC,ApR,p可得 Z-AG.1-P-C4 求张并令20,得-p d du (1-p1)2 (※) 当给定N和CsG后,由上式即可求得获最大利润的最优服务率u*。 注意:式中p=μ
(2)M/M/1/N/∞模型 在系统中顾客最大限制数为N的情况下,如系统中已有N个顾客, 则后来的顾客即被拒绝,被拒绝的概率为PN,而1-PN即为能接受服务 的概率。 单位时间实际进入服务机构的平均顾客数为λ(1-PN),在稳定状 态下,它也等于单位时间实际服务完的平均顾客数。设每服务1人能 收入G元,于是单位时间收入的期望值是λ(1-PN)G元。 纯利润: Z= λ(1-PN)G-cSμ 由公式PN= CNP0=ρNP0 可得 Z=λG· N ρ 1 1 ρ ρ N +1 − − = μ 1 1 ρ ρ N − cs − − N + 1 0, : μ , μ 求 并令 = 得 d dZ d dZ ( ) ( ) G N N s N N N c = − − + + + + + 2 1 1 1 ρ ρ 1 1 ρ ρ 当给定N和cS /G后,由上式即可求得获最大利润的最优服务率μ ﹡ 。 注意:式中ρ=λ/μ。 (※)

例9对某服务台进行实测,得到如下数据: 系统中的顾客数(n):01一23 记录到的次数(mm):161975334 平均服务时间为10分钟,服务一个顾客收益为2元,服务机构运行 单位时间成本为1元,问服务率为多少时可使单位时间平均收益最 大? 解:首先通过实测数据估计平均到达率入。 由于该系统为MWM1/N/oo模型,故有 PnIPn-1-CPol (Cn-Pop 因此, 用武i计p:”f22-060+05+04060 由=6人/小时,可得A的估计值:X=Pu=0.60×6=3.6(人/小时) 这里N=3,csG=1/2=0.5,代入公式(※)可求出p*=1.21, 故最优服务率:u*=元p=3.6/1.21=3(人1小时) 1-PN 效益分析:当6人小时,总收益Z-AG1。-C =2×3.6[1-(0.6)]s(0.6)4-1×6=0.485(元/小时) 当e3人小时,总收益Z=AG:1-。cW =2×3.6[1-(1.21)3]/[1-(1.21)4]-1×6=1.858(元/小时)
例9 对某服务台进行实测,得到如下数据: 系统中的顾客数(n): 0 1 2 3 记录到的次数(mn) : 161 97 53 34 平均服务时间为10分钟,服务一个顾客收益为2元,服务机构运行 单位时间成本为1元,问服务率为多少时可使单位时间平均收益最 大? 解:首先通过实测数据估计平均到达率λ。 由于该系统为M/M/1/N/∞模型,故有 Pn /Pn-1=CnP0 /(Cn-1P0)=ρn /ρn-1=ρ 因此,可用下式估计ρ: (0.60 0.55 0.64) 0.60 3 1 3 1 3 1 1 ρ ˆ = = + + = n= n− n m m 由μ=6人/小时,可得λ的估计值: 这里N=3, cS /G =1/2=0.5,代入公式(※)可求出ρ ﹡=1.21, 故最优服务率: μ ﹡ = 效益分析:当μ=6人/小时,总收益 Z=λG· =2×3.6[1-(0.6)3]/[1-(0.6)4]-1×6=0.485(元/小时) 当μ=3人/小时,总收益 Z=λG· =2×3.6[1-(1.21)3]/[1-(1.21)4]-1×6=1.858(元/小时) λˆ =ρ ˆ μ = 0.60 6 = 3.6(人/小时) λˆ /ρ = 3.6/1.21= 3(人/小时) μ 1 1 ρ ρ N − cs − − N + 1 μ 1 1 ρ ρ N − cs − − N + 1

7.3MWM/C模型中的最优服务台数C 仅讨论标准的MMC模型,且在稳定状态下,这时单位时间总 费用(服务费用与等待费用之和)的期望值为: Z=CsC+CL 式中C是服务台数,C是每个服务台单位时间的成本,C为每 个顾客在系统停留单位时间的费用,L是系统中顾客平均数Ls或队 列中等待的顾客平均数L。(它们都随C值的不同而不同)。因为Cs 和C,都是给定的,唯一可变是服务台数C,所以Z是C的函数Z(C), 现在是求使Z(C)达到最小的最优解C·。 因为C只取整数值,Z(C)不是连续函数,故不能用经典的微分 法。下面采用边际分析法。根据Z(C)应为最小的特点,有 Z(C)Z(C-1) Z(C)sZ(C·+1) 即∫c,C'+cwL(C)cs(C-1)+CwL(C'-1) csC'+CL(C)scs(C+1)+CL(C+1) 上式化简后得:L(C)-L(C+1)≤CsC≤L(C'-1)-L(C) 依次求C=1,2,.时L的值,并计算相邻两个L值之差,因cs/c是已知数
7.3 M/M/C模型中的最优服务台数C 仅讨论标准的M/M/C模型,且在稳定状态下,这时单位时间总 费用(服务费用与等待费用之和)的期望值为: Z=cSC+cwL 式中C是服务台数,cS是每个服务台单位时间的成本,cw为每 个顾客在系统停留单位时间的费用,L是系统中顾客平均数Ls或队 列中等待的顾客平均数Lq(它们都随C值的不同而不同)。因为cS 和cw都是给定的,唯一可变是服务台数C,所以Z是C的函数Z(C), 现在是求使Z(C)达到最小的最优解C﹡。 因为C只取整数值,Z(C)不是连续函数,故不能用经典的微分 法。下面采用边际分析法。根据Z(C﹡)应为最小的特点,有 Z(C﹡)≤ Z(C﹡-1) Z(C﹡)≤ Z(C﹡+1) 即 cSC﹡+cwL(C﹡)≤cS (C﹡-1)+cwL(C﹡-1) cSC﹡+cwL(C﹡)≤cS (C﹡+1)+cwL(C﹡+1) 上式化简后得:L(C﹡)-L(C﹡+1)≤cS /cw ≤ L(C﹡-1)-L(C﹡) 依次求C=1,2, …时L的值,并计算相邻两个L值之差,因cS /cw是已知数
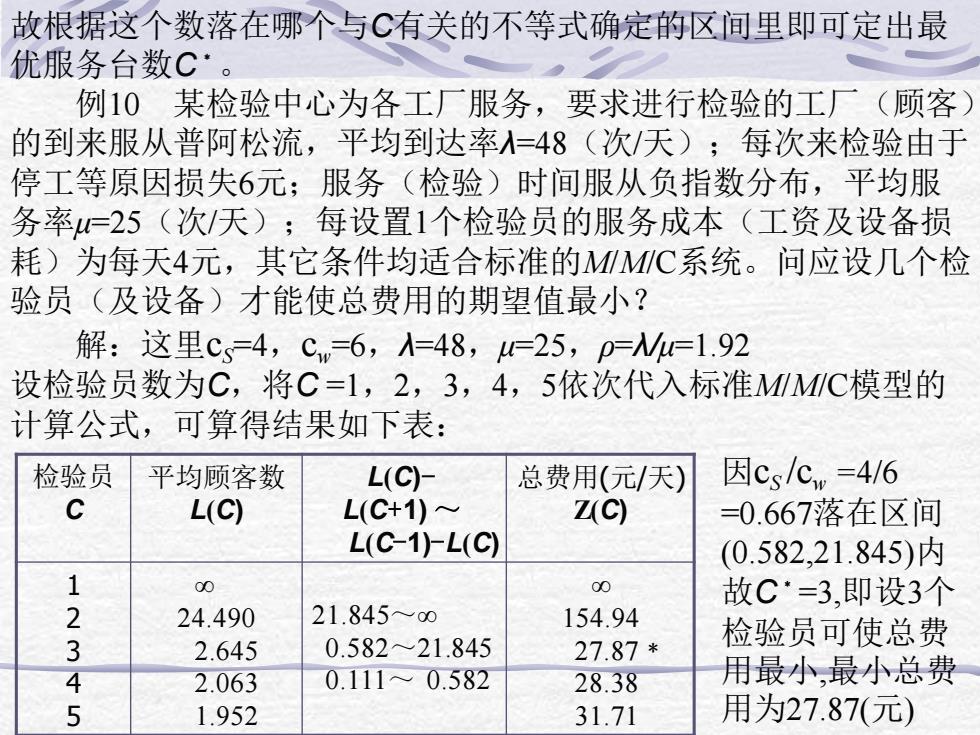
故根据这个数落在哪个与C有关的不等式确定的区间里即可定出最 优服务台数C·。 例10某检验中心为各工厂服务,要求进行检验的工厂(顾客) 的到来服从普阿松流,平均到达率=48(次/天);每次来检验由于 停工等原因损失6元;服务(检验)时间服从负指数分布,平均服 务率=25(次/天);每设置1个检验员的服务成本(工资及设备损 耗)为每天4元,其它条件均适合标准的MWMC系统。问应设几个检 验员(及设备)才能使总费用的期望值最小? 解:这里Cs=4,Cw=6,=48,u=25,p=W=1.92 设检验员数为C,将C=1,2,3,4,5依次代入标准MMC模型的 计算公式,可算得结果如下表: 检验员 平均顾客数 L(C)- 总费用(元/天) 因cs/cw=4/6 C L(C) L(C+1)~ ZC) =0.667落在区间 L(C-1厂L(C) (0.582,21.845)内 1 00 00 故C·=3,即设3个 2 24.490 21.84500 154.94 检验员可使总费 3 2.645 0.58221.845 27.87* 4 2.063 0.111~0.582 28.38 用最小,最小总费 5 1.952 31.71 用为27.87(元)
故根据这个数落在哪个与C有关的不等式确定的区间里即可定出最 优服务台数C﹡。 例10 某检验中心为各工厂服务,要求进行检验的工厂(顾客) 的到来服从普阿松流,平均到达率λ=48(次/天);每次来检验由于 停工等原因损失6元;服务(检验)时间服从负指数分布,平均服 务率μ=25(次/天);每设置1个检验员的服务成本(工资及设备损 耗)为每天4元,其它条件均适合标准的M/M/C系统。问应设几个检 验员(及设备)才能使总费用的期望值最小? 解:这里cS=4,cw=6,λ=48,μ=25,ρ=λ/μ=1.92 设检验员数为C,将C =1,2,3,4,5依次代入标准M/M/C模型的 计算公式,可算得结果如下表: 检验员 C 平均顾客数 L(C) L(C)- L(C+1) ~ L(C-1)-L(C) 总费用(元/天) Z(C) 1 2 3 4 5 ∞ 24.490 2.645 2.063 1.952 21.845~∞ 0.582~21.845 0.111~ 0.582 ∞ 154.94 27.87﹡ 28.38 31.71 因cS /cw =4/6 =0.667落在区间 (0.582,21.845)内 故C﹡=3,即设3个 检验员可使总费 用最小,最小总费 用为27.87(元)