
一、本章内容简要回顾 第五章、 在第五章中,我们首先通过两个实例(最短路线问题、 带回收的资源分配问题)引出了多阶段决策问题;接着介 绍了动态规划的基本概念和最优性原理。最优性原理用 句话概括即:最优策略的任何一部分子策略也必须是 最优的。最后详细介绍了建立动态规划数学模型的步骤。 一般来说,利用动态规划方法求解实际多阶段决策问题 第六章动态规划及应用举例 需先建立问题的动态规划模型(即动态规划基本方程), 具体步骤如下: 1将问题按时间或空间次序划分成若干阶段。有些问题 不具有时空次序,也可以人为地引进时空次序,划分阶 段g 2.正确选择状态变量xk。状态变量是动态规划模型中最 重要的参数。它()要能够描述决策过程的演变特征;(2) 要满足无后效性。即如果某阶段状态已给定后,则以后 过程的进展不受以前各状态的影响;(③)要有递推性。即 由k阶段的状态变量x及决策变量u,可以计算出k+1阶段的 状态变量Xk+1
第 五 章 、 第 六 章 动 态 规 划 及 应 用 举 例 一、本章内容简要回顾 在第五章中,我们首先通过两个实例(最短路线问题、 带回收的资源分配问题)引出了多阶段决策问题;接着介 绍了动态规划的基本概念和最优性原理。最优性原理用 一句话概括即:最优策略的任何一部分子策略也必须是 最优的。最后详细介绍了建立动态规划数学模型的步骤。 一般来说,利用动态规划方法求解实际多阶段决策问题 需先建立问题的动态规划模型(即动态规划基本方程), 具体步骤如下: ⒈将问题按时间或空间次序划分成若干阶段。有些问题 不具有时空次序,也可以人为地引进时空次序,划分阶 段。 ⒉正确选择状态变量xk。状态变量是动态规划模型中最 重要的参数。它⑴要能够描述决策过程的演变特征;⑵ 要满足无后效性。即如果某阶段状态已给定后,则以后 过程的进展不受以前各状态的影响;⑶要有递推性。即 由k阶段的状态变量xk及决策变量uk可以计算出k+1阶段的 状态变量xk+1

3.确定决策变量u及允许决策变量集合D(u)。 4.根据状态变量之间的递推关系,写出状态转移方程: Xk+=T(xk Uk(Xk)) 5.建立指标函数。一般用k(X,)描写阶段效应,(xk)表 示k~n阶段的最优子策略函数。 建立动态规划数学模型的 6.建立动态规划基本方程: f(Xk)=opt{rk(,u(X)》*东+1(Xk+1) 3 uk∈Dk(uk) 不1(xt1)=C k=n,n-1,,1 在动态规划基本方程中,,「k(X),、X三T(xu)都是已 知函数,最优子策略人(x)与1x)之间是递推关系,要 求出(x)及u,(),需要先求出不+1(k+),这就决定了应用 动态规划基本方程求最优策略总是逆着阶段的顺序进行的。 由后向前逐步计算,最终可以算出全过程的最优策略函数 骤 烧务秋、视电摄》时 还不能具体确定x+的值,所以,这就要求必须就k+1阶段 的各个可能状态计算1(&k+),因此动态规划方法不但能 求出整个问题的最优策略和最优日标值,而且还能求出决 策过程中所有可能状态的最优策略及最优目标值
建 立 动 态 规 划 数 学 模 型 的 步 骤 ❖ ⒊确定决策变量uk及允许决策变量集合Dk (uk )。 ⒋根据状态变量之间的递推关系,写出状态转移方程: xk+1=T(xk , uk (xk )) ⒌建立指标函数。一般用rk (xk , uk )描写阶段效应,fk(xk)表 示k~n阶段的最优子策略函数。 ⒍建立动态规划基本方程: fk(xk)= opt{rk (xk ,uk (xk ))﹡fk+1(xk+1)} uk∈Dk (uk ) fn+1(xn+1)=C k=n,n-1,…,1 ❖ 在动态规划基本方程中, rk (xk , uk ), xk+1=T(xk , uk )都是已 知函数,最优子策略fk(xk)与fk+1(xk+1)之间是递推关系,要 求出fk(xk)及uk (xk ),需要先求出fk+1(xk+1),这就决定了应用 动态规划基本方程求最优策略总是逆着阶段的顺序进行的。 由后向前逐步计算,最终可以算出全过程的最优策略函数 值及最优策略。另一方面,由于k+1阶段的状态xk+1=T(xk , uk )是由前面的状态xk和决策uk所形成的,在计算fk+1(xk+1)时 还不能具体确定xk+1的值,所以,这就要求必须就k+1阶段 的各个可能状态计算fk+1(xk+1),因此动态规划方法不但能 求出整个问题的最优策略和最优目标值,而且还能求出决 策过程中所有可能状态的最优策略及最优目标值

在第六章中,详细介绍了应用动态规划方法求解的八类实际问题 应重点掌握的问题 根据实际问题建立动态规划基本方程: 2、 资源分配问题; 3、 生产与存贮问题; 4、设备更新问题。 二、 典型例题分析 (带回收的资源分配问题)某厂新购某种机床125台。据估计,这 种设备5年后将被其它设备所代替。此机车如在高负荷状态下工作, 年损坏率为1/2,年利润为10万元: 如在低负荷状态下工作,年损坏 率为1/5,年利润为6万元。问应如何安排这些机床的生产负荷,才 能使5年内获得的利润最大? 本问题具有时间上的次序性,在五年计划的每一年都要作出关 于这些机床生产负荷的决策,并且一旦作出决策,不仅影响到本年 利润的多少,而且影响到下一年初完好机床数,从而影响以后各年 的利润。所以在每年初作决策时,必须将当年的利润和以后各年利 润结合起来,统筹考虑
在第六章中,详细介绍了应用动态规划方法求解的八类实际问题 ◆ 二、应重点掌握的问题 1、根据实际问题建立动态规划基本方程; 2、资源分配问题; 3、生产与存贮问题; 4、设备更新问题。 三、典型例题分析 (带回收的资源分配问题)某厂新购某种机床125台。据估计,这 种设备5年后将被其它设备所代替。此机车如在高负荷状态下工作, 年损坏率为1/2,年利润为10万元;如在低负荷状态下工作,年损坏 率为1/5,年利润为6万元。问应如何安排这些机床的生产负荷,才 能使5年内获得的利润最大? 本问题具有时间上的次序性,在五年计划的每一年都要作出关 于这些机床生产负荷的决策,并且一旦作出决策,不仅影响到本年 利润的多少,而且影响到下一年初完好机床数,从而影响以后各年 的利润。所以在每年初作决策时,必须将当年的利润和以后各年利 润结合起来,统筹考虑

解:以年为阶段,k=1,2,3,4,5 取k年初完好的机床数为状态变量x;以k年初投入高负荷运行的 机床数为决策变量u,则低负荷运行机床数是x,于是状态转移 方程为:X+=1/2u+4/5(&u)=0.8x0.3u4 以利润为目标函数,则k年利润为: 10u+6(x-ug)=4u4+6x 记(x)为k年至5年末最大总利润,则动态规划基本方程为: [f(xx)=max{4u+6x+f+1(0.8x-0.3u)} 0≤uk≤Xk (x6)=0 k=5,4,3,2,1 所以,当k=5时,有 5(x5)=max{4u5+6x+(x)}=10x3 Us-Xs 当k4时)9u6议+60.8X03】 0≤u4≤X4 =max{4u4+6x+100.8x40.3u4)} 0≤u4≤X4 = max{u4+14x4}=15x4 Uy-X4 0≤u4X4
解:以年为阶段,k=1,2,3,4,5 取k年初完好的机床数为状态变量xk ;以k年初投入高负荷运行的 机床数为决策变量uk,则低负荷运行机床数是xk-uk,于是状态转移 方程为: xk+1=1/2uk+4/5(xk-uk )=0.8xk-0.3uk 以利润为目标函数,则k年利润为: 10uk+6(xk-uk)=4uk+6xk 记fk(xk)为k年至5年末最大总利润,则动态规划基本方程为: fk(xk)=max{4uk+6xk+fk+1(0.8xk-0.3uk)} 0≤uk≤xk f6(x6)=0 k=5,4,3,2,1 所以,当k=5时,有 f5(x5)= max {4u5+6x5+f6(x6)}=10x5 u5 =x5 0≤u5≤x5 当k=4时 f4(x4)= max {4u4+6x4+f5(0.8x4-0.3u4)} 0≤u4≤x4 = max {4u4+6x4+10(0.8x4-0.3u4)} 0≤u4≤x4 = max{u4+14x4}=15x4 u4 =x4 0≤u4≤x4

◆当k=3时 5(x3)=max{4u3+6x3+f0.8x30.3u3)} 0≤u3≤x =max{4u+6x+15(0.8x-0.3ug)} 0≤u3≤X3 =max{-0.5u3+18x3}=18x3 u3=0 0≤u3≤X3 当k=2时 (x2)=max{4u+6x2+(0.8x320.3u) 典型例题分析 0≤u2≤X2 =max{4u2+6x2+18(0.8x20.3u2)} 0≤u2≤X2 =max{-1.4u2+20.4x2}=20.4x2 u2=0 当k=1时 0≤u2≤X2 f(x1)=max{4u1+6x1+万(0.8x10.3u1)} 0≤u1≤X1 =max{4u1+6x1+20.40.8x1-0.3u1)} 0≤u≤X1 =max{-2.12u1+22.32x1}=22.32x 0≤u1≤x1 =0 =22.32×125=2790(万元)
典 型 例 题 分 析 ◆当k=3时 f3(x3)= max{ 4u3+6x3+f4(0.8x3-0.3u3)} 0≤u3≤x3 = max{ 4u3+6x3+15(0.8xk-0.3uk)} 0≤u3≤x3 = max{ -0.5u3+18x3}=18x3 u3=0 0≤u3≤x3 当k=2时 f2(x2)= max{ 4u2+6x2+f3(0.8x2-0.3u2)} 0≤u2≤x2 = max{ 4u2+6x2+18(0.8x2-0.3u2)} 0≤u2≤x2 = max{-1.4u2+20.4x2}=20.4x2 u2=0 0≤u2≤x2 当k=1时 f1(x1)= max{ 4u1+6x1+f2(0.8x1-0.3u1)} 0≤u1≤x1 = max{ 4u1+6x1+20.4(0.8x1-0.3u1)} 0≤u1≤x1 = max{ -2.12u1+22.32x1}=22.32x1 0≤u1≤x1 u1=0 =22.32×125=2790(万元)

至此已算得最大总利润2790万元,再按与计算过程 相反的顺序推回去,可得最优计划如下表所示: 年份 完好机床数 高负荷机床数 低负荷机床数 k X+1=0.8x-0.3u4 Xk-Uk 典型例题分析 第一年 125 0 125 第二年 100 0 100 第三年 80 0 80 第四年 64 64 0 第五年 32 32 0
典 型 例 题 分 析 ❖ 至此已算得最大总利润2790万元,再按与计算过程 相反的顺序推回去,可得最优计划如下表所示: 年份 k 完好机床数 xk+1=0.8xk-0.3uk 高负荷机床数 uk 低负荷机床数 xk-uk 第一年 125 0 125 第二年 100 0 100 第三年 80 0 80 第四年 64 64 0 第五年 32 32 0

本章内容简要回顾 第七章 在本章中,我们首先由哥尼斯堡七桥问题引出了图论的 问题,接着给出了图与网络的基本概念:介绍了树的理论及求 最小部分树的破圈法与避圈法;然后介绍了求最短路的狄克 斯拉(Dijkstra)算法和图上标示法;介绍了求网络最大流的 标号法;最后介绍了求最小费用最大流的方法及中国邮递员 问题的解法。 图与网络分析 应重点掌握的问题 求网络的最短路问题; 求网络的最大流问题
第 七 章 图 与 网 络 分 析 ❖ 一、本章内容简要回顾 ❖ 在本章中,我们首先由哥尼斯堡七桥问题引出了图论的 问题,接着给出了图与网络的基本概念;介绍了树的理论及求 最小部分树的破圈法与避圈法;然后介绍了求最短路的狄克 斯拉(Dijkstra)算法和图上标示法;介绍了求网络最大流的 标号法;最后介绍了求最小费用最大流的方法及中国邮递员 问题的解法。 ❖ 二、应重点掌握的问题 ❖ 1、求网络的最短路问题; ❖ 2、求网络的最大流问题

典型例题分析 1、 求下图中v,到v的最短路。 第七章 3 4 方法一:狄克斯拉(Dijkstra)算法 典型例题分析 1°标p(v,)=0,其余点标T()=+0,2,3,4,5,6,7,8; 2°由刚刚获得标号的v点出发,改善与之相邻点的T标号,即 新的T(v2)=min{老的Tv2),p(v,Ho2}=min{+oo,0+3}=3 新的T(v,)=min{老的T(v),p(v,)+o3}=min{+oo,0+5}=5 新的T(v4)=min{老的T(v),p(v,)to4}=min{+oo,0+6}=6, 3°找出当前具有最小T标号的v2点,标p(=3;且记(上v 4°改善刚刚获得p标号的v点之相邻点的T标号: 新的Tv,)=min{老的T(v),p()+o23=min{5,3+1}=4, 新的7Tv,)=min{老的T(v),p(v2)+o2=min{+oo,3+7}-l0, 新的Tv)=min{老的Tvg),p(v2)+o26}=min{+oo,3+4}=7
第 七 章 典 型 例 题 分 析 ❖ 三、典型例题分析 ❖ 1、求下图中v1 到v8 的最短路。 v4 v2 3 2 6 5 v3 v5 v6 v7 v8 6 3 5 5 2 1 1 1 4 7 v 9 1 方法一:狄克斯拉(Dijkstra)算法 1°标p(v1)=0,其余点标T(vi)=+∞,i=2,3,4,5,6,7,8; 2°由刚刚获得p标号的v1点出发,改善与之相邻点的T标号,即 新的T(v2 )= min{老的T(v2 ), p (v1 )+ω12}=min{+∞,0+3}=3, 新的T(v3 )= min{老的T(v3 ), p (v1 )+ω13}=min{+∞,0+5}=5, 新的T(v4 )= min{老的T(v4 ), p (v1 )+ω14}=min{+∞,0+6}=6, 3°找出当前具有最小T标号的v2点,标p(v2 )=3;且记k(v2 )=v1 4°改善刚刚获得p标号的v2点之相邻点的T标号: 新的T(v3 )= min{老的T(v3 ), p(v2 )+ω23}=min{5,3+1}= 4, 新的T(v5 )= min{老的T(v5 ), p(v2 )+ω25}=min{+∞,3+7}=10, 新的T(v6 )= min{老的T(v6 ), p(v2 )+ω26}=min{+∞,3+4}=7
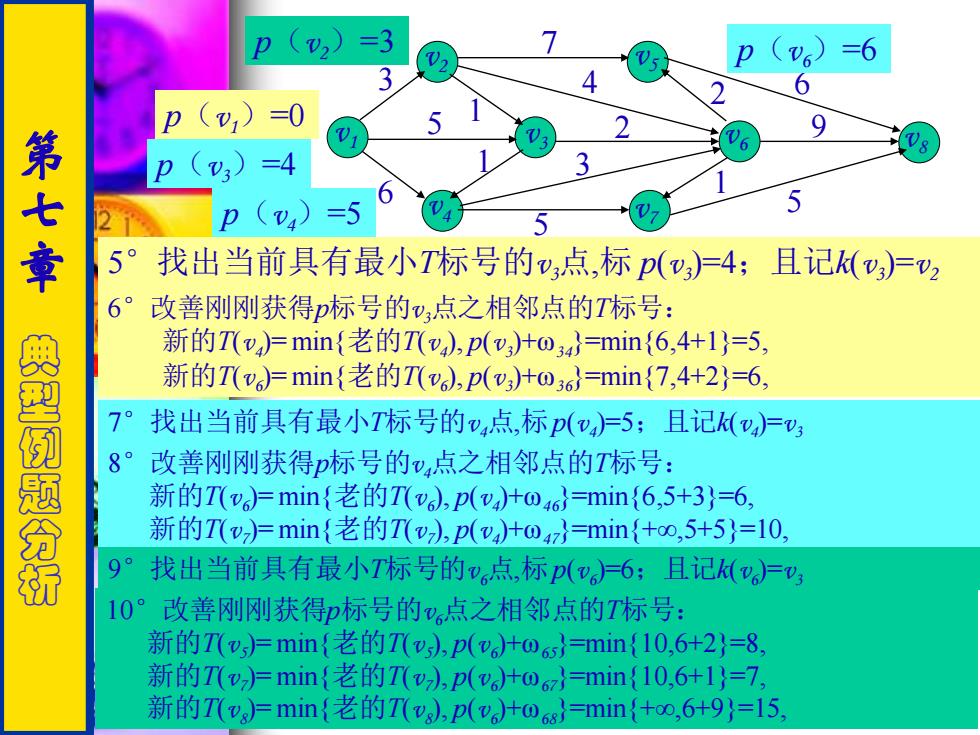
=3 6 3 6 =0 第七章 =4 =5 5 5° 找出当前具有最小T标号的v点,标p(v,)=4;且记k(v)=v 6° 改善刚刚获得p标号的v,点之相邻点的T标号: 新的T(v,)=min{老的Tv),p(v,)to34}=min{6,4+l}=5, 典型例 新的T(v,)=min{老的T(v),p(v,)+o36}=min{7,4+2}=6, 7° 找出当前具有最小T标号的v,点,标p(v戶5;且记k(v)戶V o 改善刚刚获得p标号的v,点之相邻点的T标号: 新的T(vg)=min{老的T(v),p(v)+o6}=min{6,5+3}=6 分桥 新的T(v)片min{老的T(v),p(v,)十o4}=min{+oo,5+5}=10 9°找出当前具有最小T标号的v,点,标p(v)=6;且记(v,)= 10°改善刚刚获得P标号的点之相邻点的T标号: 新的T(v,)=min{老的T(),p()+o}=min{10,6+2}=8, 新的T(v2)=min{老的T(v),p(vg)十o}=mim{10,6+l}=7 新的T(vg)=min{老的T(v),p(v,)十0=min{+o,6+9}=l5
5°找出当前具有最小T标号的v3点,标 p(v3 )=4;且记k(v3 )=v2 6°改善刚刚获得p标号的v3点之相邻点的T标号: 新的T(v4 )= min{老的T(v4 ), p(v3 )+ω34}=min{6,4+1}=5, 新的T(v6 )= min{老的T(v6 ), p(v3 )+ω36}=min{7,4+2}=6, v4 v2 3 2 6 5 v3 v5 v6 v7 v8 6 3 5 2 1 1 1 4 v 9 1 7 p(v1)=0 p(v2)=3 p(v3)=4 5 7°找出当前具有最小T标号的v4点,标p(v4 )=5;且记k(v4 )=v3 8°改善刚刚获得p标号的v4点之相邻点的T标号: 新的T(v6 )= min{老的T(v6 ), p(v4 )+ω46}=min{6,5+3}=6, 新的T(v7 )= min{老的T(v7 ), p(v4 )+ω47}=min{+∞,5+5}=10, p(v4)=5 9°找出当前具有最小T标号的v6点,标p(v6 )=6;且记k(v6 )=v3 10°改善刚刚获得p标号的v6点之相邻点的T标号: 新的T(v5 )= min{老的T(v5 ), p(v6 )+ω65}=min{10,6+2}=8, 新的T(v7 )= min{老的T(v7 ), p(v6 )+ω67}=min{10,6+1}=7, 新的T(v8 )= min{老的T(v8 ), p(v6 )+ω68}=min{+∞,6+9}=15, p(v6)=6 第 七 章 典 型 例 题 分 析

=8 =3 (v6)=6 3 =0 9 第七章 p V3》 =4 =5 5 p(2)=7 11°找出当前具有最小T标号的v,点,标p(v)=7;且记k(v)戶v 12°改善刚刚获得p标号的v,点之相邻点的T标号: 典型例 新的T(vg)=min{老的T(vg,p(v)+o8}=min{15,7+5}=12 13°找出当前具有最小T标号的v点,标p(v)=8:且记k(v)=v。 14°改善刚刚获得p标号的v点之相邻点v的T标号: 新的T八(v=min{老的7T八v),p(,)+os}=min{12,8+6}=12 分桥 15°至此,点可获得标号:p(户12;且记(v)=v 由()反向追踪,可得最短路径:V,→2→→v。→→g 因p(vg)=12,所以v,→v的最短距离为12
第 七 章 典 型 例 题 分 析 12°改善刚刚获得p标号的v7点之相邻点的T标号: 新的T(v8 )= min{老的T(v8 ), p(v7 )+ω78}=min{15,7+5}=12, 11°找出当前具有最小T标号的v7点,标 p(v7 )=7;且记k(v7 )=v6 v4 v2 3 2 6 5 v3 v5 v6 v7 v8 6 3 5 2 1 1 1 4 v 9 1 7 p(v1)=0 p(v2)=3 p(v3)=4 5 p(v4)=5 p(v6)=6 p(v7)=7 13°找出当前具有最小T标号的v5点,标 p(v5 )=8;且记k(v5 )=v6 14°改善刚刚获得p标号的v5点之相邻点v8的T标号: 新的T(v8 )= min{老的T(v8 ), p(v5 )+ω68}=min{12,8+6}=12, 15°至此,v8点可获得标号: p(v8 )=12;且记k(v8 )=v7 p(v5)=8 由k(v8 )反向追踪,可得最短路径:v1→v2→v3→v6→v7→v8 ; 因p(v8)=12,所以v1→v8 的最短距离为12