sTAb @或 级2双 第三章 运输问题 一、本章内容简要回顾 本章讨论了一类特殊的线性规划 一运输问题,介绍了求运输问题最优调运 方案的表上作业法,以及如何将产销不平衡的运输问题化为产销平衡的运输问题, 进而用表上作业法来求解。 二、应重点掌握的问题 1、用表上作业法求产销平衡运输问题的最优调运方案; 2、用表上作业法求产销不平衡运输问题的最优调运方案 96 三、典型例题分析 设有A1、A2A3三个产地生产某种物资,其产量分别为5,6,8吨,B1、B2 B3三个销地需要该物资,销量分别为4,8,6吨,又已知各产销地之间的单位运 价如下表所列,试确定总运费最少的调运方案。 产地 销地 解:产地总产量为19吨,销 B1 B2 B3 产量 地总销量为18吨,产大于销。 313 5 故虚设销地B4,令其销量b4=1 46 2 6 吨,运价C4=0,i=1,2,3,则问 3 2 85 8 题变成如下运输问题: 销量 4 86
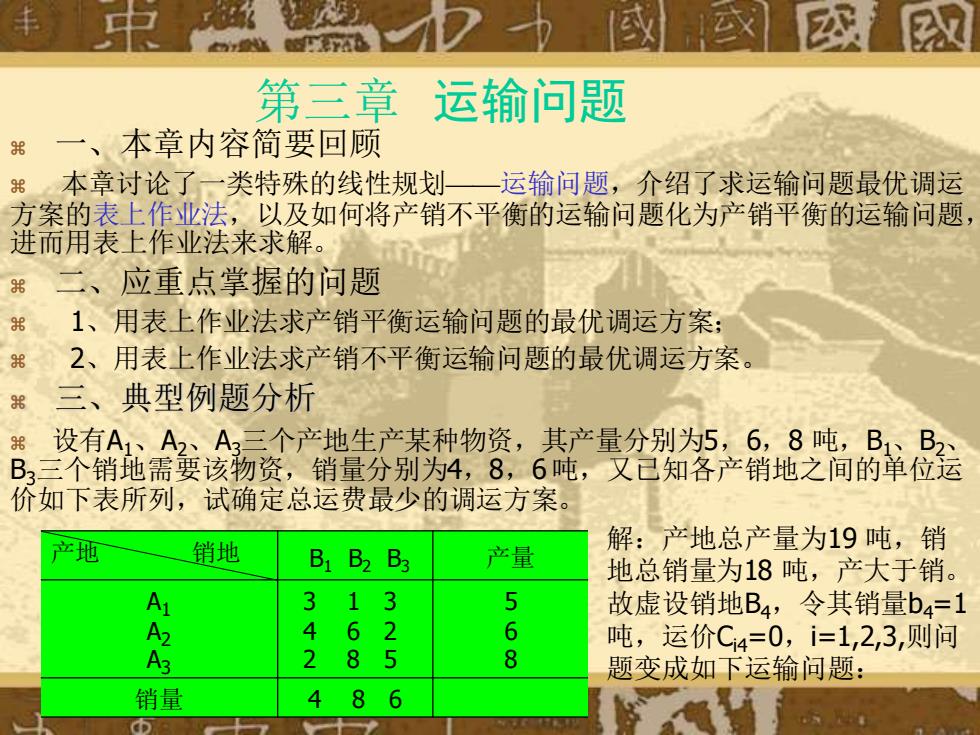
第三章 运输问题 一、本章内容简要回顾 本章讨论了一类特殊的线性规划——运输问题,介绍了求运输问题最优调运 方案的表上作业法,以及如何将产销不平衡的运输问题化为产销平衡的运输问题, 进而用表上作业法来求解。 二、应重点掌握的问题 1、用表上作业法求产销平衡运输问题的最优调运方案; 2、用表上作业法求产销不平衡运输问题的最优调运方案。 三、典型例题分析 设有A1、A2、A3三个产地生产某种物资,其产量分别为5,6,8 吨,B1、B2、 B3三个销地需要该物资,销量分别为4,8,6 吨,又已知各产销地之间的单位运 价如下表所列,试确定总运费最少的调运方案。 产地 销地 B1 B2 B3 产量 A1 A2 A3 3 1 3 4 6 2 2 8 5 5 6 8 销量 4 8 6 解:产地总产量为19 吨,销 地总销量为18 吨,产大于销。 故虚设销地B4,令其销量b4=1 吨,运价Ci4=0,i=1,2,3,则问 题变成如下运输问题:

销地 B1 B2 B3 Ba 销地 量 B1 B2 B3 B4 u 产地 产地 3 1 3 0 5 A 8) 4(10 1 0 2 4 6 2 0 6 A2 0 (-4)6 (-9 9 2 8 5 0 8 A3 4 4(5) (-7 7 销量 4 8 6 Vj -5 1-7 0 (1) 用最小元素法得初始 (3)第一次调整量0=0, 调整 方案如下表所示: 后的方案如下表所示: 销地 销地 产地 BB2 B3 B4 产地 B1 B2B3 B4 量 量 4 1 1 A2 0 56 6 0 56 4 8 4 8 3 4 销量 4 8 6 销量 4 8 6 (2)用位势法计算检验数 (4)再用位势法计算检验数 如黄表所示: 如下页黄表所示:
销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 3 1 3 4 6 2 2 8 5 0 0 0 5 6 8 销量 4 8 6 1 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 4 0 6 4 4 1 5 6 8 销量 4 8 6 1 (1)用最小元素法得初始 方案如下表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 4 0 6 4 4 1 0 9 7 vj -5 1 -7 0 (-7) (10) (-4) (-9) (8) (5) (3)第一次调整量θ=0,调整 后的方案如下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 4 6 4 4 1 0 5 6 8 销量 4 8 6 1 (2) 用位势法计算检验数 如黄表所示: (4)再用位势法计算检验数 如下页黄表所示:
, rAB 销地 B B2 B3 B4 销地 产地 B B2 B 产地 量 A (8)4 (1》 1 0 Al 3 13 0 5 A (9)(5)6 0 0 4 6 0 6 A3 4 4(-4 (-7 7 A3 2 8 5 0 8 Vj -5 1 0 销量 4 8 6 (5)第二次调整量0=1,调 (6)再用位势法计算检验数如 整后的方案如下表所示: 下表所示: 销地 B B2 B: 产地 Ba 销地 量 产地 B1 B2 B3 B4 A 5 5 (8)5(8) (7 0 A A 6 0 6 A2 (2)(-2)6 0 77 A 4 3 1 8 A 4 3(3) 销量 4 86 1-5 -7
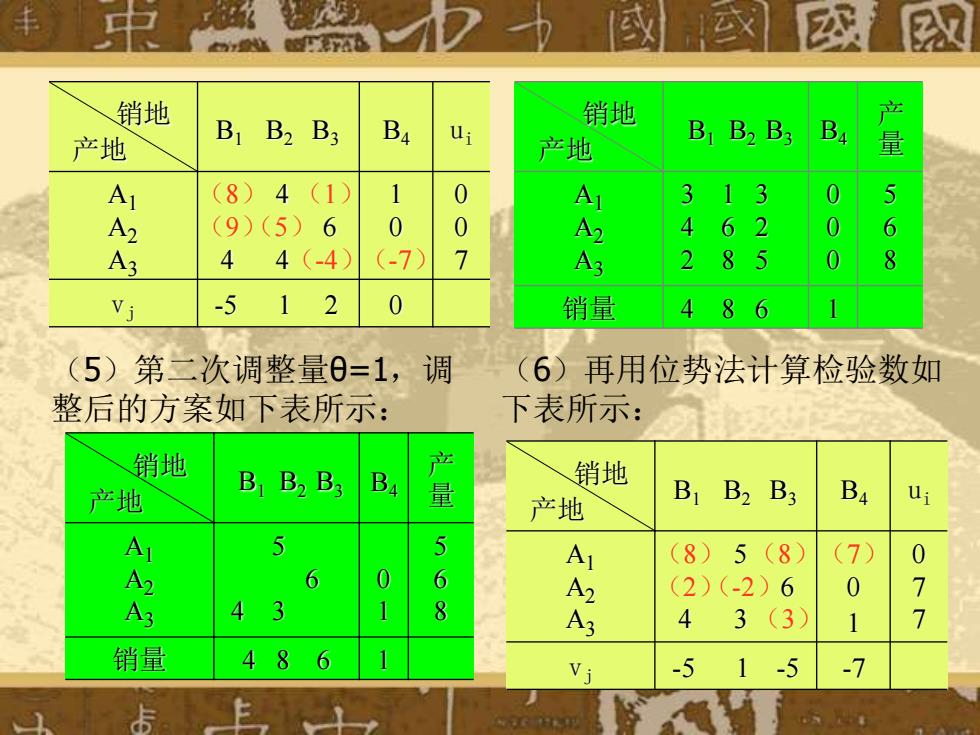
销地 产地 B1 B2 B3 B4 ui A1 A2 A3 4 6 4 4 1 0 0 0 7 vj -5 1 2 0 (-4)(-7) (9) (8) (5) (1) 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 3 1 3 4 6 2 2 8 5 0 0 0 5 6 8 销量 4 8 6 1 (5)第二次调整量θ=1,调 整后的方案如下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 5 6 4 3 0 1 5 6 8 销量 4 8 6 1 (6)再用位势法计算检验数如 下表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 5 6 4 3 0 1 0 7 7 vj -5 1 -5 -7 (8) (8)(7) (2)(-2) (3)
(7)第三次调整量0=0, 调整后的方案如下表所示: 销地 产地 BB2 B3 B4 量 销地 B B2 B3 B 产地 量 Al 3 13 0 5 4 6 2 0 6 5 43 2 8 0 8 A 0 6 6 3 8 销量 4 8 6 4 销量 4 8 6 (8)再用位势法计算检验 数如下表所示: 左表中所有检验数均非负。所 销地 产地 B B2 B3 Ba u 以己是最优解。最小总运费: A (8) 5 (6 (7) 0 5×1+6×2+4×2+3×8+1×0 A2 (4)0 6 (2 5 =49 4 3 (1) 1 7 Vj -5 1-3 -7
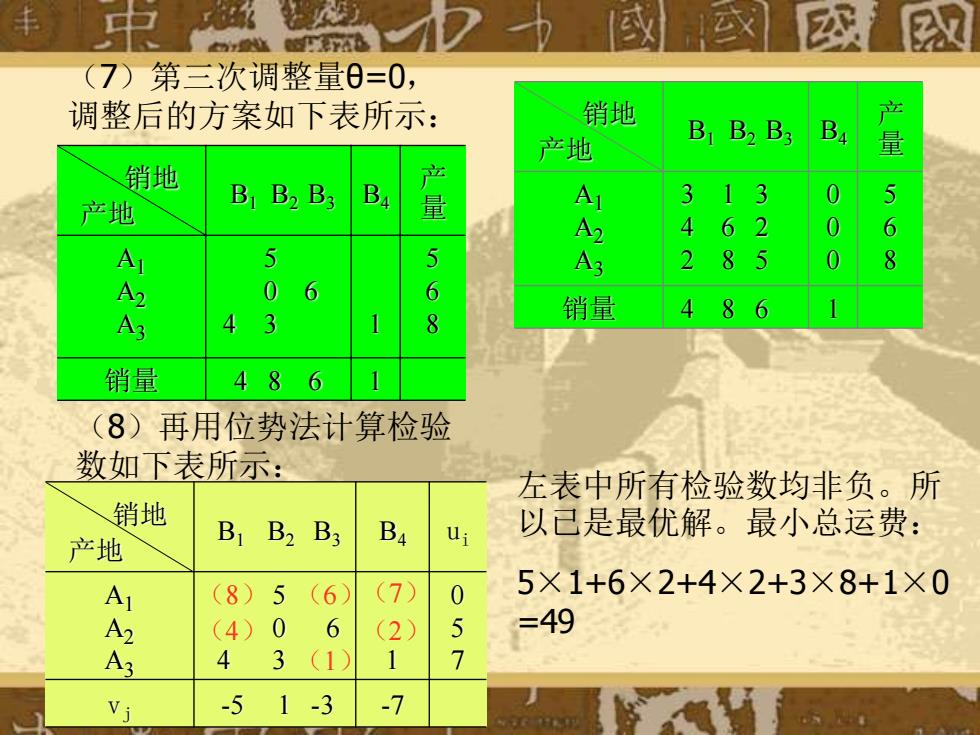
(7)第三次调整量θ=0, 调整后的方案如下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 5 0 6 4 3 1 5 6 8 销量 4 8 6 1 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 3 1 3 4 6 2 2 8 5 0 0 0 5 6 8 销量 4 8 6 1 (8)再用位势法计算检验 数如下表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 5 0 6 4 3 1 0 5 7 vj -5 1 -3 -7 (8) (4) (6) (1) (7) (2) 左表中所有检验数均非负。所 以已是最优解。最小总运费: 5×1+6×2+4×2+3×8+1×0 =49

第四章 整数规划 、本章内容简要回顾 本章讨论了取整数解的特殊线性规划一整数规划间题。先介绍 了求解一般整数规划问题的分枝定界法;又介绍了求解纯整数规划 的割平面法;接着介绍了求解“01型整数规划”的隐枚举法。最后 较详细地讨论了“0-1型整数规划”的特例一指派问题的求解方法 (匈牙利法)。 二、应重点掌握的问题 8 1、求解“0-1型整数规划”的隐枚举法: 2、求解指派问题的匈牙利法。 三、典型例题分析
第四章 整数规划 一、本章内容简要回顾 本章讨论了取整数解的特殊线性规划—整数规划问题。先介绍 了求解一般整数规划问题的分枝定界法;又介绍了求解纯整数规划 的割平面法;接着介绍了求解“0-1型整数规划”的隐枚举法。最后 较详细地讨论了“0-1型整数规划”的特例—指派问题的求解方法 (匈牙利法)。 二、应重点掌握的问题 1、求解“0-1型整数规划”的隐枚举法; 2、求解指派问题的匈牙利法。 三、典型例题分析

1、用隐枚举法求解下述0-1规划: maxZ-3xj-2x2+5xs 解:调整xX的顺序,使目标函数中变量 X1+2x2X32 的系数呈递增(不减)的顺序,则问题变 X1+4x2+X3 为: X1+X2 ≤3 maxZ=-2x2+3x+5x3 2X2+X1-X3≤2 ① 4X2+x3≤6 4x2+x1+x3≤4 ② X1,X2,x3=0或1 x+X1 ≤3 ③ 解 约束条件 4x2 +x3≤6 ④ (X2,,X3)》 标 ① ②③④ X1,X2,X3=0或1 按二进制数码从小到大的顺序排列并检查 (000) 0 √VV 各个解,先计算解的目标值,若目标值小 (001) 5 于目前可行解最好的目标值,则不必检查 (010 是否满足约束条件,当所有解被检查完毕 (011 就可判断出最优解。计算结果可列表表示, 8 见左表。 (100) (101) 最终得到最优解:x=1,20, (110) X3=1,最优值:Z=8 (111
1、用隐枚举法求解下述0-1规划: maxZ=3x1 -2x2+5x3 x1+2x2 -x3 ≤2 x1+4x2 +x3 ≤4 x1+ x2 ≤3 4x2 +x3 ≤6 x1 ,x2 ,x3 =0或1 解 (x2,x1,x3) 目 标 值 约束条件 ① ② ③ ④ (0 0 0) 0 √ √ √ √ (0 0 1) 5 √ √ √ √ (0 1 0) - - - - - (0 1 1) 8 √ √ √ √ (1 0 0) - - - - - (1 0 1) - - - - - (1 1 0) - - - - - (1 1 1) 6 - - - - 解:调整x1 ,x2的顺序,使目标函数中变量 的系数呈递增(不减)的顺序,则问题变 为: maxZ=-2x2 +3x1+5x3 2x2+x1 -x3≤2 ① 4x2 +x1 +x3≤4 ② x2+x1 ≤3 ③ 4x2 +x3≤6 ④ x1 ,x2 ,x3=0或1 按二进制数码从小到大的顺序排列并检查 各个解,先计算解的目标值,若目标值小 于目前可行解最好的目标值,则不必检查 是否满足约束条件,当所有解被检查完毕, 就可判断出最优解。计算结果可列表表示, 见左表。 最终得到最优解:x1=1,x2=0, x3=1,最优值:Z=8

,@级2双 2、今欲指派张王李赵四人加工A、B、C、D四种不同的零件, 每人加工四种零件所需要的时间如下表所示,问应该派谁加工何种 零件可使总的花费时间最少? 零件 A B D 4 6 5 王李 6 10 7 8 11 9 9 3 8 A 解:先变换效率矩阵,然后圈出不同行不同列的0元素,结果如下: 4 658 「021 41 02037 6 107 8 0412 040 7 8 119 0142 013 3 8 6051 6 )40 由于不同行不同列的0元素仅有3个,所以要调整效率矩阵,使 之出现新的0元素
2、今欲指派张王李赵四人加工A、B、C、D四种不同的零件, 每人加工四种零件所需要的时间如下表所示,问应该派谁加工何种 零件可使总的花费时间最少? 零件 人 A B C D 张 王 李 赵 4 6 5 8 6 10 7 8 7 8 11 9 9 3 8 4 解:先变换效率矩阵,然后圈出不同行不同列的0元素,结果如下: 6 0 4 0 0 1 3 1 0 4 0 1 0 2 0 3 6 0 5 1 0 1 4 2 0 4 1 2 0 2 1 4 9 3 8 4 7 8 11 9 6 10 7 8 4 6 5 8 ○ ∕ ∕ ○ ∕ ○ ∕ 由于不同行不同列的0元素仅有3个,所以要调整效率矩阵,使 之出现新的0元素

或汉 用最少的直线覆盖效率矩阵中的0元素: 02 3 1°给没有“回”的行打 “V” 4 2° 给打“√”行中的0元素所在列打“√ 3°给打“√”列中“回”所在的行打 “V 4°重复2°、3°的工作,直至打不出新 6 0 止; 5°对没打“√”行画横线;对打“V”列画 竖线,则可将效率矩阵中所有0元素覆盖 010 2 6°以未被划去的最小元素为调整量0(=1),调 0300 整效率矩阵使之出现更多0元素(打“V”行各元 00 素减0;打“√”列各元素加0)。而后,再重新圈 出不同行且不同列的0元素,进行再指派。结果 7 50 如左图所示。 由于O的个数已达n=4个,所以令所对应的=1,其余=0, 即得最优解。即最优指派方案为:张一C;王一A;李一D:赵一B。 所需最少总时间为:5+6+9+3=23。注意,本例的最优方案不唯 一, 张一A;王C;李一B;赵一D也是最优方案
用最少的直线覆盖效率矩阵中的0元素: 6 0 4 0 0 1 3 1 0 4 0 1 0 2 0 3 ○ ∕ ∕ ○ ∕ ○ ∕ √ √ √ 1°给没有“◎”的行打“√”; 2°给打“√”行中的0元素所在列打“√”; √ √ 3°给打 “√”列中“◎”所在的行打“√”; 4°重复2°、3°的工作,直至打不出新“√” 止; 5°对没打“√”行画横线;对打“√”列画 竖线,则可将效率矩阵中所有0元素覆盖。 7 0 5 0 0 0 3 0 0 3 0 0 ∕ 0 1 ○ 0 2 ○ ∕ ∕ ∕ ○ ∕ ∕ ○ 6°以未被划去的最小元素为调整量θ(=1),调 整效率矩阵使之出现更多0元素(打“√”行各元 素减θ;打“√”列各元素加θ)。而后,再重新圈 出不同行且不同列的 0 元素,进行再指派。结果 如左图所示。 由于◎的个数已达n=4个,所以令◎所对应的xij =1,其余xij =0, 即得最优解。即最优指派方案为:张—C;王—A;李—D;赵—B。 所需最少总时间为:5+6+9+3=23。注意,本例的最优方案不唯一, 张—A;王—C;李—B;赵—D也是最优方案