s5多服务台排队系统模型(MM/C) MMC系统是指顾客按普阿松流输入,服务时间为 负指数分布,有C个服务台的单队多台并列服务系统。 它的结构见图10一7。在这种系统,顾客到达系统后排 成一个队列,然后到能给以服务的服务台接受服务,而 每个服务台的服务时间都服从相同参数的负指数分布, 服务完毕后顾客自动离去。 离去 服务台1 顾客到达 离去 服务台2 离去 图10一7 服务台C 由于顾客的到达间隔和服务时间都服从负指数分布,所以 这种系统象MMM系统一样,能直接利用生灭过程的计算 方法计算稳态概率。下面分别讨论MW/C模型的几种类型
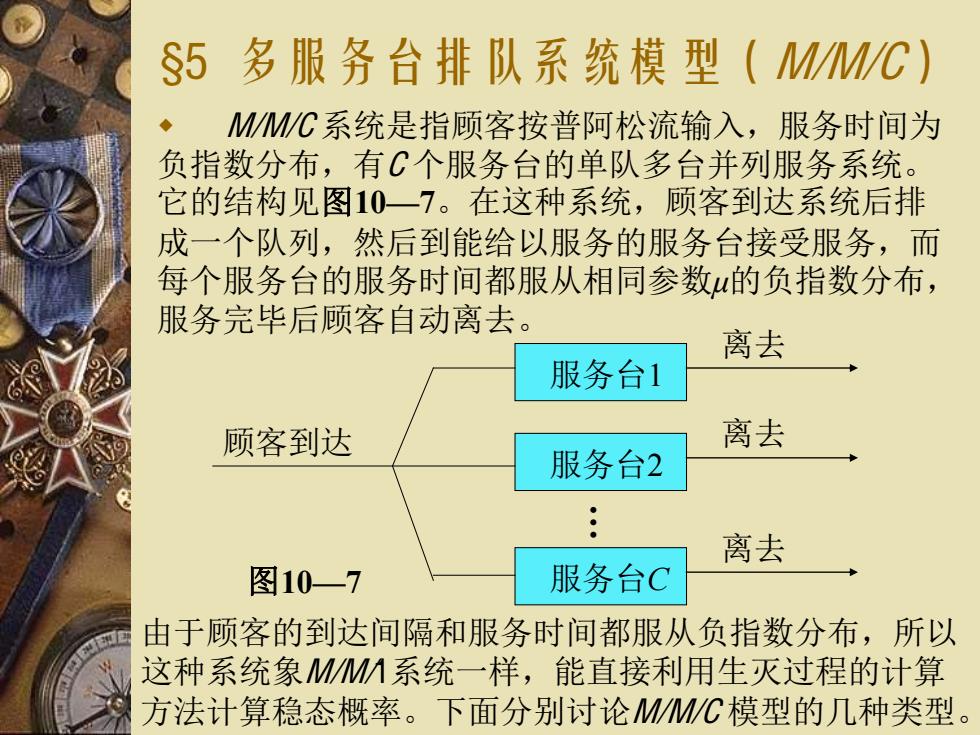
§5 多服务台排队系统模型(M/M/C) M/M/C 系统是指顾客按普阿松流输入,服务时间为 负指数分布,有C 个服务台的单队多台并列服务系统。 它的结构见图10—7。在这种系统,顾客到达系统后排 成一个队列,然后到能给以服务的服务台接受服务,而 每个服务台的服务时间都服从相同参数μ的负指数分布, 服务完毕后顾客自动离去。 服务台1 离去 服务台2 离去 服务台C 离去 … 顾客到达 由于顾客的到达间隔和服务时间都服从负指数分布,所以 这种系统象M/M/1系统一样,能直接利用生灭过程的计算 方法计算稳态概率。下面分别讨论M/M/C 模型的几种类型。 图10—7

5.1M/M/C/ool/oo模型 这是系统对顾客无限制,顾客源也无限制的多服务台 模型,其状态转移图如下: 2u 3u (C-1)w Cu Cu Cu 图10—8 入,=A n=0,1,2, nu 当n=1,2,,C-1 Un= lCu 当n2C 入-入-2…10 当m=2”c Cn nln-1“a aCn-c,当n≥C
5.1 M/M/C/∞/∞模型 这是系统对顾客无限制,顾客源也无限制的多服务台 模型,其状态转移图如下: 0 1 2 C-1 C C+1 λ λ λ λ λ λ λ μ 2μ 3μ (C-1)μ Cμ ● ● ● ● ● ● ● ● ● ● ● 图10—8 Cμ Cμ λn =λ n=0,1,2, … nμ 当n=1,2, …, C-1 Cμ 当n≥C μn = Cn = ( ) ( ) , n≥C C!C μ λ , n = 1,2, ,C 1. n! μ λ n - c n n 当 当 - = n n-1 1 n-1 n-2 0 μμ μ λλ λ

设p=WCu<1,(当2I时,系统无稳定状态) 则 P02 +交 入/ p当n=l2,c- n! Pn=CnPo= 当n≥C CIcn-co c+j CI BTPR C1-p2 Ls=Lg+Wu Ws-Ls/A W。=LgA=Ws-l/
设ρ=λ/Cμ<1,(当ρ≥1时,系统无稳定状态) 则 P0= ( ) ( ) 1 ρ 1 n! c! c c n n n μ λ μ c 1 λ n c n 0 1 n 0 1 C C 1 − + • = + − = = = − Pn= CnP0= ( ) P , n C n c C!C P , n 1,2, ,c 1 n! 0 0 n n μ λ μ λ − = − 当 当 Lq ( ) ( ) ( ) ( ) 2 j C!1 ρ ρ c ρ C! c ρ c C c C!C c j μ λ μ λ − = = − + = = = = = = + = 0 j 0 0 j 0 0 j 0 c j n c n P j P n-c P jP j P c Ls =Lq+λ/μ Ws =Ls /λ Wq =Lq /λ=Ws-1/μ

例4某公用电话亭有两台电话机,来打电话的人按普 阿松流到达,平均每小时24人,假定每次电话通话时间服 从负指数分布,平均为2分钟,求该系统各项指标。 解:p=/C=24÷2÷30=0.4 gglo8oao4a7 电话空闲的概率: 电话亭内有一个顾客的概率: P=(Wμ)P。=0.8X3/7=12/35 排队打电话的平均人数: La-V P 0 0.8×049605 1p)220-0.49 电话亭内打电话及等待的总平均人数: Ls=Lg+Wμ=16/105+0.8=20/21 每个顾客在电话亭内平均停留时间: W、=LsA=20/21÷24=5/126(小时)=50/21(分钟)
例4 某公用电话亭有两台电话机,来打电话的人按普 阿松流到达,平均每小时24人,假定每次电话通话时间服 从负指数分布,平均为2分钟,求该系统各项指标。 解:ρ=λ/Cμ=24÷2÷30=0.4 电话空闲的概率: ( ) ( ) 1 1 1 0.8 (0.8) /2(1 0.4) 3/7 2 1 ρ 1 c! c μ λ c 1 n 0 n! n μ λ = + + − = − + • − = P0= 电话亭内有一个顾客的概率: P1=(λ/μ)P0=0.8×3/7=12/35 排队打电话的平均人数: ( ) ( ) ( ) 16/105 21 0.4 7 3 0.8 0.4 1 ρ ρ C! c 2 2 2 μ λ = − = − = Lq P0 电话亭内打电话及等待的总平均人数: Ls=Lq+λ/μ=16/105+0.8=20/21 每个顾客在电话亭内平均停留时间: Ws =Ls /λ=20/21÷24=5/126(小时)=50/21(分钟)
每个顾客排队等候打电话的平均时间: W。=Lg小=16/105÷24=2/315(小时)=8/21(分钟) 来打电话的人需要等待的概率: P(W。>0)=1-PoP=1-3/7-12/35=8/35 MWM/C型系统与C个MM/1型系统的比较 现在就上面的例子加以说明,如果原问题中其它条件不变! 但顾客到达后在每台电话前各排一队,且进入队列后坚持不 变,这就形成了2个MM1系统,而每个队列的平均到达率为 入=2=12(人/小时)。计算这个MWMW1模型,并与上面的 MM/C模型比较,结果如下表所示: 指标 模型 M/M/1 M/M/2 从表上各 服务台空闲概率Po 3/5 3/7 指标对比 顾客必须等待的概率 12/35 8/35 可以看出, 平均队长Lg MWM/C模 28/105 16/105 型比C个 平均顾客数Ls 14/21 20/21 M/M/1模 平均逗留时间Wg 70/21分钟 50/21分钟 型有显著 平均等待时间Wg 28/21分钟 8/21分钟 优越性
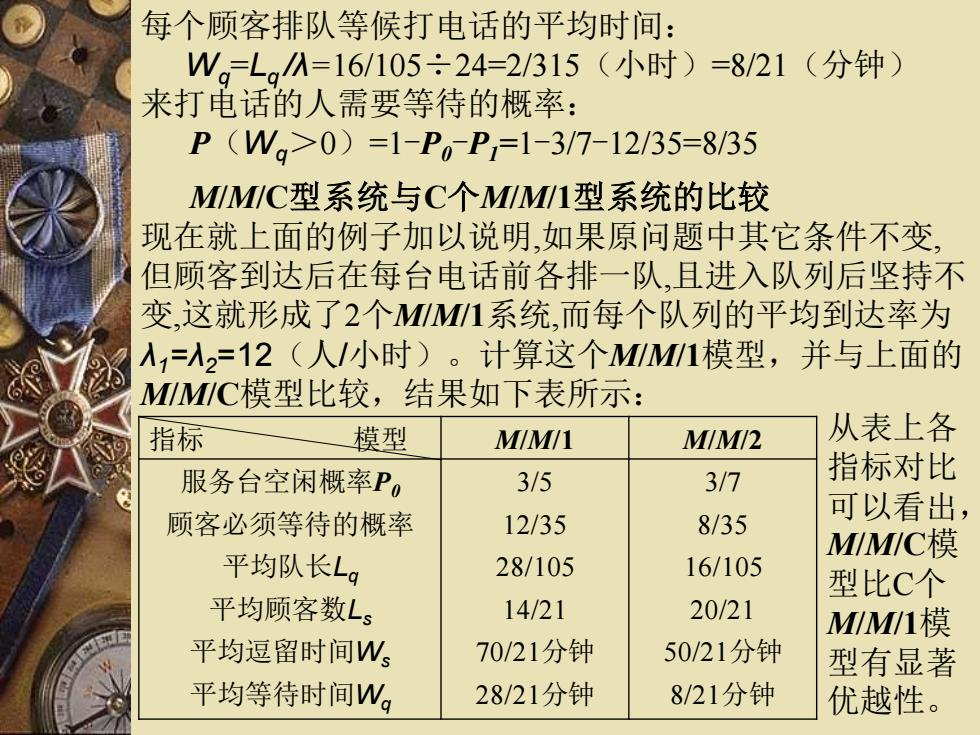
每个顾客排队等候打电话的平均时间: Wq =Lq /λ=16/105÷24=2/315(小时)=8/21(分钟) 来打电话的人需要等待的概率: P(Wq>0)=1-P0-P1=1-3/7-12/35=8/35 M/M/C型系统与C个M/M/1型系统的比较 现在就上面的例子加以说明,如果原问题中其它条件不变, 但顾客到达后在每台电话前各排一队,且进入队列后坚持不 变,这就形成了2个M/M/1系统,而每个队列的平均到达率为 λ1=λ2=12(人/小时)。计算这个M/M/1模型,并与上面的 M/M/C模型比较,结果如下表所示: 指标 模型 M/M/1 M/M/2 服务台空闲概率P0 3/5 3/7 顾客必须等待的概率 12/35 8/35 平均队长Lq 28/105 16/105 平均顾客数Ls 14/21 20/21 平均逗留时间Ws 70/21分钟 50/21分钟 平均等待时间Wq 28/21分钟 8/21分钟 从表上各 指标对比 可以看出, M/M/C模 型比C个 M/M/1模 型有显著 优越性

5.2M/M/CIN/ooi模型(系统容量有限制情形) 该系统的容量限制为N(C),当系统中顾客数已达 到N时,再来的顾客即被拒绝,其它条件与MM/C/oo/oo模 型相同。系统的状态转移图如下: 入 ● 2u 3u (C-1)u Cu Cu Cu Cu 图10—9 这里 nA当n=0,1,2,…,N-1;n0 当≥N n,当n=1,2,,C Cu,当n=C+l,,N 入-入-2…0 Y”当n=1,2C Po 其中p=/Cu≠1
5.2 M/M/C/N/∞模型(系统容量有限制情形) 该系统的容量限制为N(N≥C),当系统中顾客数已达 到N时,再来的顾客即被拒绝,其它条件与M/M/C/∞/∞模 型相同。系统的状态转移图如下: 0 1 2 C-1 C λ λ λ λ λ λ λ μ 2μ 3μ (C-1)μ Cμ ● ● ● ● ● ● ● ● 图10—9 Cμ Cμ N-1 N Cμ λ 这里 λn =λ 当 n=0,1,2, …,N-1;λn=0 当n≥N μn = = n n-1 1 n-1 n-2 0 μμ μ λλ λ ( ) ( ) = + + = , 1, 2, , . μ λ ! 1 , 1,2, , . μ λ ! 1 - n C C N CC n C n n n c n 当 当 P0= 其中ρ=λ/Cμ≠1 ( ) ( ) 1 ρ ρ ρ ρ C! C n! N n 0 N n 0 n 1 c μ λ c c c c n n n 1 C C 1 − − + • = + = = = + Cn = nμ,当n=1,2, …, C Cμ,当n=C+1, …,N

于是 Pn=CnPo= ee当-2-,c g"p当C<n<N CI LneR-3 PCNC】 C1-p)2 因为队长有限制,所以顾客平均到达率并不等于入, 记Ae#为有效到达率,则Aer=》nPn=人岁P(1-Pw) n=0 n=0 由此可以算得 Ls=Lg+Aen/u=Lg+A(1-PN)/u Wg-Lg八ef=Lg/(1-Pw) Ws-Wg+1/u 特别当N=C时,该系统成为损失制服务模型, 例如街头的 停车场就不允许排队等待空位,这时 n! Po,n曰l,2,sc Lg=0,Wg=0,Ws=1/μ,Ls=(1-PN)/w
于是 Pn= CnP0= ( ) P , C n N C! ρ c C P , n 1,2, ,C n! Cρ 0 0 n n = 当 当 Lq ( ) ( ) ( ) 1 ρ (N C)ρ (1 ρ ) C!1 ρ c ρ Cρ N C N C 2 N N C − − − − − = = = − − − = + = 0 j 0 c j n c n P n-c P jP 因为队长有限制,所以顾客平均到达率并不等于λ, 记λeff 为有效到达率,则λeff = = = λ(1-PN) − = = N N 1 λ λ n 0 n n 0 nPn P 由此可以算得 Ls =Lq+λeff /μ=Lq+λ(1-PN)/μ Wq =Lq /λeff =Lq / λ(1-PN) Ws =Wq+1/μ 特别当N=C时,该系统成为损失制服务模型,例如街头的 停车场就不允许排队等待空位,这时 ( ) = c n n 0 n! μ λ 1 P0= ,Pn= CnP0= P ,n 1,2, ,c n! 0 n μ λ = Lq =0,Wq=0,Ws=1/μ,Ls= λ(1-PN)/μ

例5某单位电话交换台有一台200门内线的总机。已 知在上班的八小时内,有20%的内线分机平均每四十分钟 要一次外线电话,80%的分机平均隔两小时要一次外线电 话,又知从外单位打来的电话呼唤平均每分钟一次,设外 线通话时间平均三分钟,以上两个时间均属负指数分布。 如果要求电话接通率为95%,问该交换台应设置多少外线? 解:(1)来到电话交换台的呼唤有两类:一是各分机往 外打的电话,二是从外单位打进来的电话。 前一类A1=(0.2×60/40+0.8×1/2)×200=140(次/小时) 后一类A2=60(次/小时) 根据普阿松分布的性质,来到交换台的总呼唤流仍为普阿 松流,其参数=元1+几2=200。 (2)这是一个具有多个服务台带损失制的服务系统,要 使电话接通率为95%,就要使损失率低于5%,亦即 ) ≤0.05 nl
例5 某单位电话交换台有一台200门内线的总机。已 知在上班的八小时内,有20%的内线分机平均每四十分钟 要一次外线电话,80%的分机平均隔两小时要一次外线电 话,又知从外单位打来的电话呼唤平均每分钟一次,设外 线通话时间平均三分钟,以上两个时间均属负指数分布。 如果要求电话接通率为95%,问该交换台应设置多少外线? 解:⑴来到电话交换台的呼唤有两类:一是各分机往 外打的电话,二是从外单位打进来的电话。 前一类λ1 =(0.2×60/40+0.8×1/2)×200=140(次/小时) 后一类λ2 =60(次/小时) 根据普阿松分布的性质,来到交换台的总呼唤流仍为普阿 松流,其参数λ=λ1+λ2=200。 ⑵这是一个具有多个服务台带损失制的服务系统,要 使电话接通率为95%,就要使损失率低于5%,亦即 ( ) ( ) = c n n c C n 0 ! ! μ λ μ λ PC = ≤0.05

问题中u=60/3=20(次/小时),Wu=200/20=10,可以通过列 表计算,来求得满足要求的C。 C ) c Pe 0 1.0 1.0 1.000 1 10.0 11.0 0.909 2 50.0 61.0 0.820 3 166.7 227.7 0.732 4 416.7 644.4 0.647 5 833.3 1477.7 0.564 6 1388.9 2866.6 0.485 7 1984.1 4850.7 0.409 8 2480.2 7330.9 0.388 9 2755.7 10086.6 0.273 10 2755.7 12842.3 0.215 11 2505.2 15347.5 0.163 12 2087.7 17435.2 0.120 13 1605.9 19041.1 0.084 14 1147.1 20188.2 0.057 15 764.7 20952.9 0.036
问题中μ=60/3=20(次/小时), λ/μ=200/20=10,可以通过列 表计算,来求得满足要求的C。 C PC 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1.0 10.0 50.0 166.7 416.7 833.3 1388.9 1984.1 2480.2 2755.7 2755.7 2505.2 2087.7 1605.9 1147.1 764.7 1.0 11.0 61.0 227.7 644.4 1477.7 2866.6 4850.7 7330.9 10086.6 12842.3 15347.5 17435.2 19041.1 20188.2 20952.9 1.000 0.909 0.820 0.732 0.647 0.564 0.485 0.409 0.388 0.273 0.215 0.163 0.120 0.084 0.057 0.036 ( ) ! μ λ c C ( ) = c n n n 0 ! μ λ

根据上表计算结果可以看出,要使外线接通率达95%, 交换台应设置不少于15条的外线。 说明:①计算中没有考虑外单位打来电话时,内线是 否占用,也没有考虑分机打外线时,对方是否占线。 ②当电话一次打不通时,就要打两次、三次、,因 此实际呼唤次数要远远高于计算次数,因此实际接通率也 要比95%低得多
根据上表计算结果可以看出,要使外线接通率达95%, 交换台应设置不少于15条的外线。 说明:①计算中没有考虑外单位打来电话时,内线是 否占用,也没有考虑分机打外线时,对方是否占线。 ②当电话一次打不通时,就要打两次、三次、…,因 此实际呼唤次数要远远高于计算次数,因此实际接通率也 要比95%低得多