
§2到达间隔与服务时间的分布 解决排队问题首先要判断顾客到达间隔和服务时间的分布,现 在介绍排队模型中常见的几种理论分布。 2.1普阿松流 令Pn(t,t2)表示在时间区间[t,t2)(t2>t)内有n个顾客到 达的概率,当P,(t,t2)和乎下列三个条件时,我们说顾客的到达 形成普阿松流。 (1)无后效性。在不相重叠的时间区间内顾客到达数是相互独立 的。 (2)平稳性。对充分小的△t,在时间区间[t,t+△0内有1个顾客到 达的概率与t无关,而与△t成正比,即 P,(t,t+△t)=入△t+o(△t) 其中入>0是常数,它表示单位时间有一个顾客到达的概率;⊙ (△t)是当△t0时,关于△t的高阶无穷小量。 (3)普通性。对于充分小的△t,在时间区间[t,t+△t)内有2个或 2个以上顾客到达的概率极小,即 SPn(t,+△t)=0(△t)
n=2 §2 到达间隔与服务时间的分布 ⚫ 解决排队问题首先要判断顾客到达间隔和服务时间的分布,现 在介绍排队模型中常见的几种理论分布。 ⚫ 2.1 普阿松流 令Pn(t1 ,t2)表示在时间区间[t1 ,t2)(t2>t1)内有n 个顾客到 达的概率,当Pn(t1 ,t2)和乎下列三个条件时,我们说顾客的到达 形成普阿松流。 ⑴无后效性。在不相重叠的时间区间内顾客到达数是相互独立 的。 ⑵平稳性。对充分小的△t,在时间区间[t,t+△t)内有1个顾客到 达的概率与t无关,而与△t 成正比,即 P1(t,t+△t)=λ△t+ο(△t) 其中 λ>0是常数,它表示单位时间有一个顾客到达的概率; ο (△t)是当△t→0时 ,关于△t的高阶无穷小量。 ⑶普通性。对于充分小的△t,在时间区间[t,t+△t)内有2个或 2个以上顾客到达的概率极小,即 Pn(t,t+△t)=ο(△t)

根据普阿松流的三个条件,我们来讨论在[O,)内顾客到达数 N(t)的概率分布。 将长度为t的时间区段分成n等份,△t=n,当n→∞时,△t为 充分小,在△t内可能会有1个顾客到达,其概率为入△t=入tn,在△t 内也可能没有顾客到达,其概率为1-入公1-t加。 记[0,t)内有k个顾客到达的概率为Pk(t) 则P(tD=iC1- = k=0,1,2,… 由于普阿松流与实际流的近似性,更由于普阿松流容易处理, 因此排队论中大量研究的是普阿松流情况。事实上,应用排从论来 研究实际问题到日前为止也主要限于普阿松流,对非普阿松流的情 况,大多还没有得到满意的分析解
根据普阿松流的三个条件,我们来讨论在[0,t)内顾客到达数 N(t)的概率分布。 将长度为t 的时间区段分成n等份,△t =t/n,当n→∞时,△t为 充分小,在△t内可能会有1个顾客到达,其概率为λ△t=λt/n,在△t 内也可能没有顾客到达,其概率为 1-λ△t=1-λt/n 。 记[0,t)内有k个顾客到达的概率为Pk(t), 则 Pk(t)= = = k =0,1,2, … 由于普阿松流与实际流的近似性,更由于普阿松流容易处理, 因此排队论中大量研究的是普阿松流情况。事实上,应用排队论来 研究实际问题到目前为止也主要限于普阿松流,对非普阿松流的情 况,大多还没有得到满意的分析解。 k n k n n λ t 1 n C λ t lim k n − → − k n k n n λ t 1 n λ t k! n n 1 n k 1 lim − → − − − + ( ) ( ) λ t k n n k e k! λ t n λ t lim1 k! λ t − → − =

2.2负指数分布 在实际排队系统中服务时间的概率分布可以是各种形式,但在 排队论中,最容易进行数学处理、最常用的一种重要分布是负指数 分布。设T是一个以μ为参数的负指数分布,它的概率密度函数为: ue-ut,t≥0 f)= 0,tK0 它的分布函数是 P{T≤t}=1-ew (t>0) 数学期望E(T)=1/μ,方差D(T)=1/u2 负指数分布具有下列性质: (1)由条件概率公式容易证明 P{T>什s|T>s=P{T>t) 这个性质称为无记忆性或马尔可夫性。若T表示排队系统中顾客到 达的间隔时间,那么这个性质说明一个顾客到达所需的时间与过去 一个顾客到达所需的时间s无关,所以这种情况下的顾客到达是纯随 机的。 (2)当输入过程是普阿松流时,相继到达的顾客的间隔时间T服 从负指数分布
2.2 负指数分布 在实际排队系统中服务时间的概率分布可以是各种形式,但在 排队论中,最容易进行数学处理、最常用的一种重要分布是负指数 分布。设T是一个以μ为参数的负指数分布,它的概率密度函数为: = − 0,t 0 μe ,t 0 f t μt T 它的分布函数是 P{T≤t}=1-e -μt (t>0) 数学期望E(T)=1/μ,方差D(T)=1/ μ2 负指数分布具有下列性质: ⑴由条件概率公式容易证明 P{T > t+s|T>s}=P{T>t} × 这个性质称为无记忆性或马尔可夫性。若T表示排队系统中顾客到 达的间隔时间,那么这个性质说明一个顾客到达所需的时间与过去 一个顾客到达所需的时间s无关,所以这种情况下的顾客到达是纯随 机的。 ⑵当输入过程是普阿松流时,相继到达的顾客的间隔时间T服 从负指数分布

事实上,对于普阿松流,若顾客到达的间隔时间T≤,则在O,t) 内至少有1个顾客到达,从而 P{T≤t}=1-Po(t)=leM (t>0) 即T服从参数为入的负指数分布。 因此,相继到达的间隔时间是独立且为相同参数的负指数分布, 与输入过程为普阿松流(参数为))是等价的。 根据负指数分布与普阿松流的关系可以推出,当服务机构对顾 客的服务时间服从参数为的负指数分布,如果服务机构处于忙期, 则该服务机构的输出,即服务完毕离开服务机构的顾客数将是眼从 普阿松分布的普阿松流。其中μ为每个顾客的平均服务时间,也是 顾客相继离开的间隔
事实上,对于普阿松流,若顾客到达的间隔时间T≤t,则在[0,t) 内至少有1个顾客到达,从而 P{T≤t}=1- P0(t) =1-e -λt (t>0) 即T服从参数为λ的负指数分布。 因此,相继到达的间隔时间是独立且为相同参数的负指数分布, 与输入过程为普阿松流(参数为λ)是等价的。 根据负指数分布与普阿松流的关系可以推出,当服务机构对顾 客的服务时间服从参数为μ的负指数分布,如果服务机构处于忙期, 则该服务机构的输出,即服务完毕离开服务机构的顾客数将是服从 普阿松分布的普阿松流。其中μ为每个顾客的平均服务时间,也是 顾客相继离开的间隔

2.3爱尔朗分布 当服务工作由若干项串联组成,对每位顾客的总服务时间T是 随机变量,关于T的概率分布,可以证明如下结论: 设 1°服务工作由k个服务项目串联而成。 2°第i个项目的服务时间v是随机变量,服从参数ku的负指数 分布,i=1,2,…,k. 3°,,.k是相互独立的随机变量,那么,总服务时间 T=vtv2+…+. 服从密度函数为b -知t≥0 k-1 的概率分布,称T服从k阶爱尔朗分布。 数学期望E(T)=1/,方差D(T)=1/ku2
2.3 爱尔朗分布 当服务工作由若干项串联组成,对每位顾客的总服务时间T是 随机变量,关于T的概率分布,可以证明如下结论: 设 1°服务工作由k个服务项目串联而成。 2°第i 个项目的服务时间vi 是随机变量,服从参数kμ的负指数 分布,i =1,2, …,k. 3° v1,v2,… vk是相互独立的随机变量,那么,总服务时间 T=v1+v2+…+ vk 服从密度函数为 的概率分布,称T服从k阶爱尔朗分布。 数学期望E(T)=1/μ,方差D(T)=1/ kμ2 ( ) t 0 k 1! kμ kμ t b t , kμ t k 1 k e − = − −

§3生灭过程 ●】 生灭过程是用来处理输入为普阿松流,服务时间为负指数分布 这样一类最简单排队模型的方法。 ·什么是生灭过程?举例来说,假如有一堆细菌,每个细菌在时 间△t内分裂成两个的概率为入△t+o(△t)在△时间内死亡的概 率为μ△t+o(△t),各个细菌在任何时段内分裂利死亡都是独立的, 并且把细菌的分裂和死亡都看作一个事件的话,则在t内发生两个 或两个以上事件的概率为o(△t)。假如已知初始时刻细菌的个数, 要问经过时间t后细菌将变成多少个?如把细菌的分裂看成是个新 顾客的到达,细菌的死亡看成一个服务完毕的顾客离去,则生灭 程恰好反映了一个排队服务系统的瞬时状态W()一 在时刻服务 系统中的顾客数,将怎样随时间而变化。 ·在生灭过程中,生与死的发生都是随机的,它们的平均发生率 依赖于现有的细菌数,即系统现处的状态。假定: ·(a)给定N(t)=n,到下一个生(顾客到达)的间隔时间是具 有参数入n(n=0,1,2,.)的负指数分布;
§3 生灭过程 ⚫ 生灭过程是用来处理输入为普阿松流,服务时间为负指数分布 这样一类最简单排队模型的方法。 ⚫ 什么是生灭过程?举例来说,假如有一堆细菌,每个细菌在时 间△t内分裂成两个的概率为λ△t+ο(△t),在△t时间内死亡的概 率为μ△t+ο(△t),各个细菌在任何时段内分裂和死亡都是独立的, 并且把细菌的分裂和死亡都看作一个事件的话,则在△t内发生两个 或两个以上事件的概率为ο(△t)。假如已知初始时刻细菌的个数, 要问经过时间t后细菌将变成多少个?如把细菌的分裂看成是一个新 顾客的到达,细菌的死亡看成一个服务完毕的顾客离去,则生灭过 程恰好反映了一个排队服务系统的瞬时状态N(t)——在时刻t服务 系统中的顾客数,将怎样随时间t而变化。 ⚫ 在生灭过程中,生与死的发生都是随机的,它们的平均发生率 依赖于现有的细菌数,即系统现处的状态。假定: ⚫ (a)给定N(t)=n,到下一个生(顾客到达)的间隔时间是具 有参数λn(n=0,1,2, …)的负指数分布;
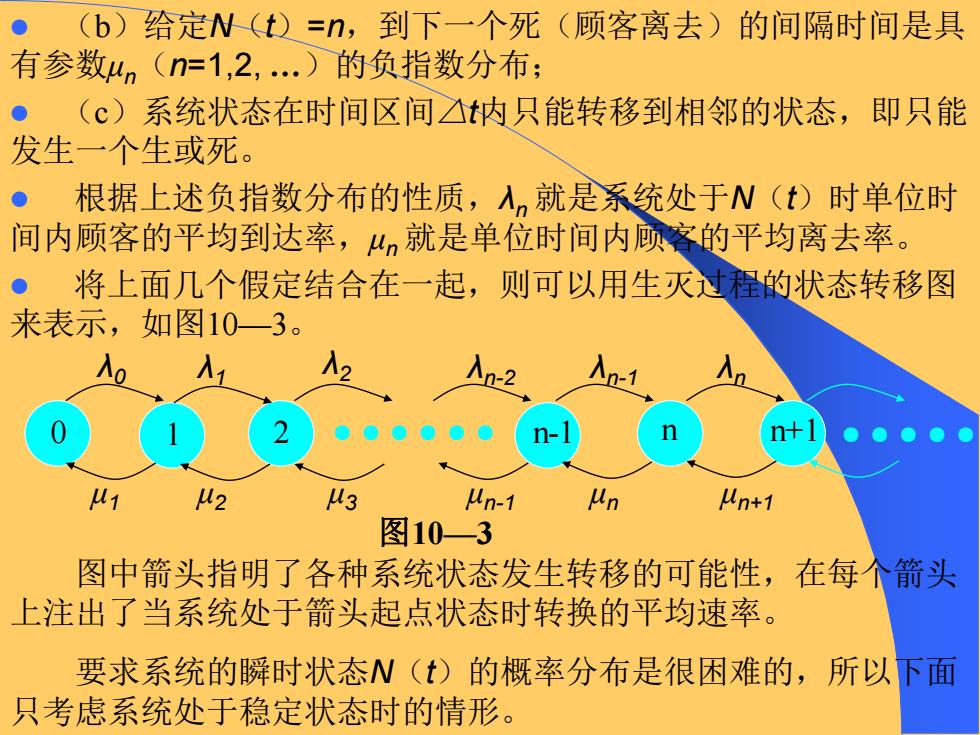
● (b)给定N()=n,到下一个死(顾客离去)的间隔时间是具 有参数4n(n=1,2,.)的负指数分布; ● (c)系统状态在时间区间△t内只能转移到相邻的状态,即只能 发生一个生或死。 ● 根据上述负指数分布的性质,入就是系统处于N(t)时单位时 间内顾客的平均到达率,4n就是单位时间内顾客的平均离去率。 ● 将上面几个假定结合在一起,则可以用生灭过程的状态转移图 来表示,如图10一3。 2 u3 Wn-1 un n+1 图103 图中箭头指明了各种系统状态发生转移的可能性,在每个箭头 上注出了当系统处于箭头起点状态时转换的平均速率。 要求系统的瞬时状态N(t)的概率分布是很困难的,所以下面 只考虑系统处于稳定状态时的情形
⚫ (b)给定N(t)=n,到下一个死(顾客离去)的间隔时间是具 有参数μn(n=1,2, …)的负指数分布; ⚫ (c)系统状态在时间区间△t内只能转移到相邻的状态,即只能 发生一个生或死。 ⚫ 根据上述负指数分布的性质,λn 就是系统处于N(t)时单位时 间内顾客的平均到达率,μn 就是单位时间内顾客的平均离去率。 ⚫ 将上面几个假定结合在一起,则可以用生灭过程的状态转移图 来表示,如图10—3。 ● ● ● ● ● ● ● ● ● ● ● λ0 λ1 λn-2 λn-1 λn λ2 μ1 μ2 μ3 μn-1 μn μn+1 0 1 2 n-1 n n+1 图10—3 图中箭头指明了各种系统状态发生转移的可能性,在每个箭头 上注出了当系统处于箭头起点状态时转换的平均速率。 要求系统的瞬时状态N(t)的概率分布是很困难的,所以下面 只考虑系统处于稳定状态时的情形

先考虑系统处于某一特定状态N(t)=n(n=0,1,2,.)。我 们计算过程进入这个状态和离开这个状态的次数,因为在同一时刻 这两个事件都只能发生一次,因此进入和离开这个状态的次数或者 相等,或者刚好差一次。对稳定系统来说,在很长一段时间内,进 出系统的顾客数保持平衡,即对系统的任何状态N(t)=n (=0,1,2,.),进入事件率(单位时间平均到达的顾客数)等于 离去事件率(单位时间平均离开的顾客数),这就是所谓输入率等 于输出率的原则。用来表示这个原则的方程称作系统的状态平衡方 程。下面就是要通过建立系统的平衡方程来处理一些比较简单的排 队模型。 设处于状态时系统的稳定状态概率为Pi。先考虑=0的状态, 状态0的输入仅仅来自状态1,而从状态1进入状态0的平均转换率为 41,因此从状态1进入状态0的输入率为uP1,又从其它状态直接进 入状态0的概率为0,所以状态0的总输入率为u1P1。根据输入率等 于输出率的原则,4P1=入oPo。 同理,根据输入率等于输出率的原则,对系统的各个状态,可 以建立起下述状态平衡方程组:
先考虑系统处于某一特定状态N(t)= n (n=0,1,2, …)。我 们计算过程进入这个状态和离开这个状态的次数,因为在同一时刻 这两个事件都只能发生一次,因此进入和离开这个状态的次数或者 相等,或者刚好差一次。对稳定系统来说,在很长一段时间内,进 出系统的顾客数保持平衡,即对系统的任何状态N(t)= n (n=0,1,2, …),进入事件率(单位时间平均到达的顾客数)等于 离去事件率(单位时间平均离开的顾客数),这就是所谓输入率等 于输出率的原则。用来表示这个原则的方程称作系统的状态平衡方 程。下面就是要通过建立系统的平衡方程来处理一些比较简单的排 队模型。 设处于状态i时系统的稳定状态概率为Pi。先考虑n=0的状态, 状态0的输入仅仅来自状态1,而从状态1进入状态0的平均转换率为 μ1 ,因此从状态1进入状态0的输入率为μ1P1,又从其它状态直接进 入状态0的概率为0,所以状态0的总输入率为μ1P1。根据输入率等 于输出率的原则,μ1P1=λ0P0。 同理,根据输入率等于输出率的原则,对系统的各个状态,可 以建立起下述状态平衡方程组:

入n-2 ●●●●● u1 u3 n-1 un un+1 图10—3 ● 41P1=0P0 ● oP0+u2P2=(入+u1)P1 ● 入P1+3P3=(2+u2)P2 ● n-2Pn2 +UnPn=(n-1t4n-1)Pn1 ●n-Pn-1unt1Pn+F(ntn)Pn 从上述方程组可解得: P=(Aolu)Po 入入0 P2=(入2)P1= P3=(八243)P2=
⚫ μ1P1=λ0P0 ⚫ λ0P0+μ2P2=(λ1+μ1)P1 ⚫ λ1P1+μ3P3=(λ2+μ2)P2 ………… ⚫ λn-2Pn-2+μnPn =(λn-1+μn-1)Pn-1 ⚫ λn-1Pn-1+μn+1Pn+1=(λn+μn)Pn … ……… ● ● ● ● ● ● λ0 λ1 λn-2 λn-1 λn λ2 μ1 μ2 μ3 μn-1 μn μn+1 0 1 2 n-1 n n+1 ● ● ● ● ● 图10—3 从上述方程组可解得: P1=(λ0 /μ1)P0 P2=(λ1 /μ2)P1= P0 P3=(λ2 /μ3)P2 = P0 …………… 2 1 1 0 μ μ λ λ 3 2 1 2 1 0 μ μ μ λ λ λ

Pn2(n-n入Pn-1= 入n入n2 儿ln-l4i ·如令 c 入n-人n-2人0 (n=1,2,.》 nn- 则以上各式可以写为一个通式: Pn=Cn Po (n=1,2,.》 00 因为 三P-CPw=1 (C0=1) 。所以有 1 P02 00 C 求得P后,可以推得Pn, (=1,2,.) 在输入是普阿松流,服务时间为负指数分布的服务系统中,顾 客到达和离去的规律符合生灭过程的条件,因此,MM类型的服务 系统可以用生灭过程方法求得稳态概率,进而求出排队系统的各项 指标:L。(系统中顾客数的平均值):L。(队列中顾客数的平均 值);W。(每个顾客在系统中平均逗留的时间);W。(每个顾客 在队列中平均逗留的时间)
⚫ Pn =(λn-1 /μn)Pn-1 = P0 ………………… ⚫ 如令 Cn= (n=1,2, …) 则以上各式可以写为一个通式: ⚫ Pn = CnP0 (n=1,2, …) ⚫ 因为 Pn= CnP0=1 (C0=1) ⚫ 所以有 P0= n n-1 1 n-1 n-2 0 μ μ μ λ λ λ n n-1 1 n-1 n-2 0 μ μ μ λ λ λ n=0 n=0 n=0 Cn 1 求得P0后,可以推得 Pn,(n=1,2, …)。 在输入是普阿松流,服务时间为负指数分布的服务系统中,顾 客到达和离去的规律符合生灭过程的条件,因此,M/M类型的服务 系统可以用生灭过程方法求得稳态概率,进而求出排队系统的各项 指标:Ls(系统中顾客数的平均值); Lq(队列中顾客数的平均 值);Ws(每个顾客在系统中平均逗留的时间);Wq(每个顾客 在队列中平均逗留的时间)