
第六章 动态规划应用举例 §2生产与存贮问题 生产与存贮问题是实际生产中经常遇到的问题,大量生产可以 降低成本,但当超过市场需求时,就造成积压,增加库存费用,完 全按市场需求安排生产虽然没有库存费用,但由于开工不足或加班 加点造成生产成本得的增加。因此,合理利用库存调节产量,满足 需求是十分有意义的。所谓生产存贮问题,就是一个生产部门如何 在己知生产成本、库存费用和各阶段市场需求条件下,决定各阶段 产量,使计划期内的费用总和为最小的问题。原材料采购部门也会 遇到同样问题,在那里需要确定各时期的采购量,使得计划期内总 费用最小。 这类问题通常是一个多阶段决策问题,可以用动态规划方法求 解。在动态模型中,以时期为阶段;取各时期初的库存量为状态变 量;选各阶段的产量(或采购量)为决策变量,在确定决策变量时 一般要考虑需求量、生产能力、库存限制等因素;指标函数取生产 (或采购)费用。 下面举例说明该问题的求解方法
第六章 动态规划应用举例 §2 生产与存贮问题 生产与存贮问题是实际生产中经常遇到的问题,大量生产可以 降低成本,但当超过市场需求时,就造成积压,增加库存费用,完 全按市场需求安排生产虽然没有库存费用,但由于开工不足或加班 加点造成生产成本得的增加。因此,合理利用库存调节产量,满足 需求是十分有意义的。所谓生产存贮问题,就是一个生产部门如何 在已知生产成本、库存费用和各阶段市场需求条件下,决定各阶段 产量,使计划期内的费用总和为最小的问题。原材料采购部门也会 遇到同样问题,在那里需要确定各时期的采购量,使得计划期内总 费用最小。 这类问题通常是一个多阶段决策问题,可以用动态规划方法求 解。在动态模型中,以时期为阶段;取各时期初的库存量为状态变 量;选各阶段的产量(或采购量)为决策变量,在确定决策变量时 一般要考虑需求量、生产能力、库存限制等因素;指标函数取生产 (或采购)费用。 下面举例说明该问题的求解方法
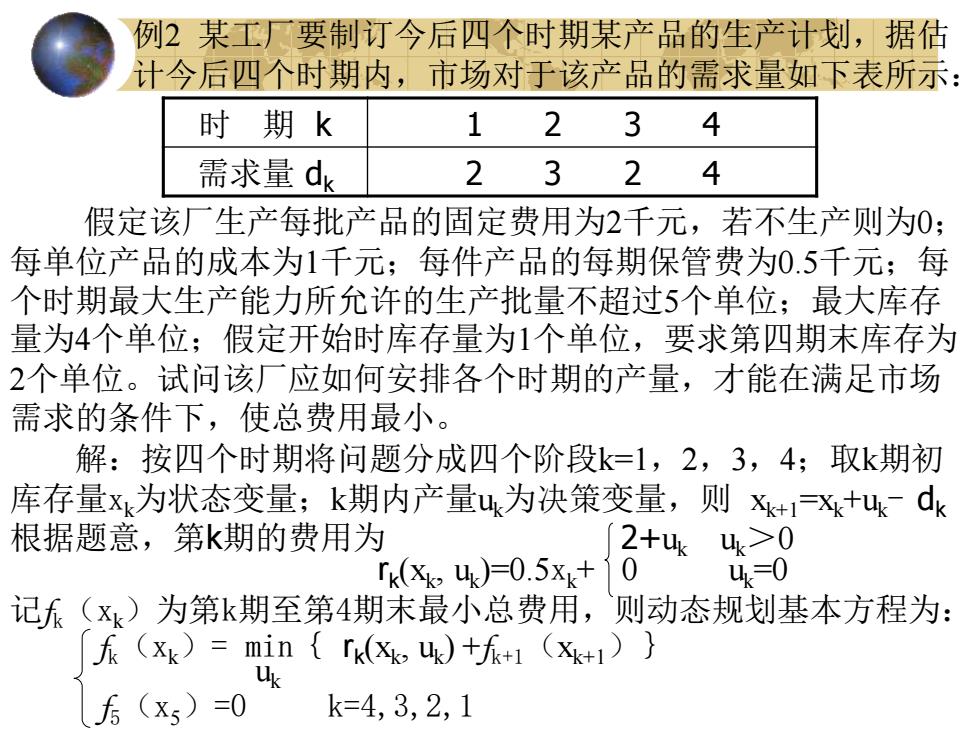
例2某工厂要制订今后四个时期某产品的生产计划,据估 计今后四个时期内,市场对于该产品的需求量如下表所示: 时期k 1 2 3 4 需求量dk 2324 假定该厂生产每批产品的固定费用为2千元,若不生产则为0: 每单位产品的成本为1千元;每件产品的每期保管费为0.5千元;每 个时期最大生产能力所允许的生产批量不超过5个单位;最大库存 量为4个单位;假定开始时库存量为1个单位,要求第四期末库存为 2个单位。试问该厂应如何安排各个时期的产量,才能在满足市场 需求的条件下,使总费用最小。 解:按四个时期将问题分成四个段k=1,2,3,4;取k期初 库存量x为状态变量;k期内产量u为决策变量,则Xk+=X+udk 根据题意,第k期的费用为 2+k 4>0 rk(xkuk)=0.5xk+ 0 4=0 记人(xk)为第k期至第4期末最小总费用,则动态规划基本方程为: 无(xk)=min{rk(风)+东+1(x+1)】 后(x5)=0 k=4,3,2,1
例2 某工厂要制订今后四个时期某产品的生产计划,据估 计今后四个时期内,市场对于该产品的需求量如下表所示: 时 期 k 1 2 3 4 需求量 dk 2 3 2 4 假定该厂生产每批产品的固定费用为2千元,若不生产则为0; 每单位产品的成本为1千元;每件产品的每期保管费为0.5千元;每 个时期最大生产能力所允许的生产批量不超过5个单位;最大库存 量为4个单位;假定开始时库存量为1个单位,要求第四期末库存为 2个单位。试问该厂应如何安排各个时期的产量,才能在满足市场 需求的条件下,使总费用最小。 解:按四个时期将问题分成四个阶段k=1,2,3,4;取k期初 库存量xk为状态变量;k期内产量uk为决策变量,则 xk+1=xk+uk- dk 根据题意,第k期的费用为 2+uk uk>0 rk (xk , uk )=0.5xk+ 0 uk=0 记fk(xk)为第k期至第4期末最小总费用,则动态规划基本方程为: fk(xk)= min{ rk (xk , uk ) +fk+1(xk+1)} uk f5(x5)=0 k=4,3,2,1

=4 注意:Xk+1Xu-dk,.x4Xu4+d4=2+4u4 而u4≤5,∴.X4=1,2,3,4 于是由动态规划基本方程人(xk)=min{「k(Xk,k)+东+1(Xk+1) 有:4(1)=0.5×1+2+5=7.5(注意:u4=6-X4) u(1)=5 f(2)=0.5×2+2+4=7 u4(2)=4 f4(3)=0.5×3+2+3=6.5 山4(3)=3 斤(4)=0.5×4+2+2=6 u4(2)=2 k=3 3=0,1,2,3,4注意:X3+u3-d3X21,而d3=2, .u≥3-x3,又x≤4,.u3≤min{5,6-x3} 于是有: 0.5×0+2+3+f(1) 5+7.5 §(0)=min0.5×0+2+4+f(2)=min6+7 =12.5 0.5×0+2+5+f(3) 7+6.5 u3(0)=3 0.5×1+2+2+f(1) 4.5+7.5 5(1)=min0.5×1+2+3+f(2) =min 5.5+7 =12 0.5×1+2+4+f(3) 6.5+6.5 0.5×1+2+5+f(4) 7.5+6 3(1)=2
k=4 注意:xk+1=xk+uk-dk,∴x4=x5-u4+d4=2+4-u4, 而u4≤5,∴x4=1,2,3,4 于是由动态规划基本方程fk(xk)= min{ rk (xk , uk ) +fk+1(xk+1)} 有: f4(1)=0.5×1+2+5=7.5(注意:u4=6-x4) u4(1)=5 f4(2)=0.5×2+2+4=7 u4(2)=4 f4(3)=0.5×3+2+3=6.5 u4(3)=3 f4(4)=0.5×4+2+2=6 u4(2)=2 k=3 x3 =0,1,2,3,4 注意:x3+u3-d3=x4≥1,而d3=2, ∴u3≥3-x3,又x4≤4, ∴u3≤min{5,6-x3} 于是有: 0.5×0+2+3+f4(1) 5+7.5 f3(0)=min 0.5×0+2+4+f4(2)=min 6+7 =12.5 0.5×0+2+5+f4(3) 7+6.5 u3(0)=3 0.5×1+2+2+f4(1) 4.5+7.5 f3(1)=min 0.5×1+2+3+f4(2)=min 5.5+7 =12 0.5×1+2+4+f4(3) 6.5+6.5 0.5×1+2+5+f4(4) 7.5+6 u3(1)=2

注意:ug23-x3,u3≤min{5,6-X3},X3+u3-2-x4 0.5×2+2+1+f(1) 4+7.5 ∴.6(2)=min0.5×2+2+2+f (2)=min 5+7 =11.5 0.5×2+2+3+f(3) 6+6.5 0.5×2+2+4+f(4) 7+6 u3(2)=1 0.5×3+0+f(1) 1.5+7.5 5(3)=minJ0.5×3+2+1+f(2) =min 4.5+7 =9 0.5X3+2+2+f(3) 5.5+6.5 0.5×3+2+3+f斤(4) 6.5+6 u3(3)=0 0.5×4+0+f(2) 2+7 5(4)=min{0.5×4+2+1+f(3)=min 5+6.5 =9 0.5×4+2+2+f(4) 6+6 3(4)=0
注意:u3≥3-x3,u3≤min{5,6-x3}, x3+u3-2=x4 0.5×2+2+1+f4(1) 4+7.5 ∴ f3(2)=min 0.5×2+2+2+f4(2)=min 5+7 =11.5 0.5×2+2+3+f4(3) 6+6.5 0.5×2+2+4+f4(4) 7+6 u3(2)=1 0.5×3+0+f4(1) 1.5+7.5 f3(3)=min 0.5×3+2+1+f4(2)=min 4.5+7 =9 0.5×3+2+2+f4(3) 5.5+6.5 0.5×3+2+3+f4(4) 6.5+6 u3(3)=0 0.5×4+0+f4(2) 2+7 f3(4)=min 0.5×4+2+1+f4(3)=min 5+6.5 =9 0.5×4+2+2+f4(4) 6+6 u3(4)=0

k=2 x2=0,1,2,3,4 注意:0≤X2u2d2x3≤4,而d2=3, ∴.3-x2≤u2≤min{5,7-x2} 于是有: 0.5×0+2+3+5(0) 5+12.5 五(0)=min0.5×0+2+4+5(1)=min6+12 =17.5 0.5×0+2+5+5(2) 7+11.5 2(0)=3 0.5×1+2+2+f6(0) 4.5+12.5 £(1)=min 0.5×1+2+3+5(1) =min 5.5+12 =16.5 0.5×1+2+4+5(2) 6.5+11.5 0.5×1+2+5+5(3) 7.5+9 u2(1)=5 0.5×2+2+1+5 (0) 4+12.5 0.5×2+2+2+5(1) 5+12 龙(2)=min{0.5×2+2+3+5(2) =min 6+11.5=16 0.5×2+2+4+5(3) 7+9 0.5×2+2+5+5 (4) 8+9 山(2)=4
k=2 x2 =0,1,2,3,4 注意:0≤x2+u2-d2=x3≤4,而d2=3, ∴3-x2≤u2≤min{5,7-x2} 于是有: 0.5×0+2+3+f3(0) 5+12.5 f2(0)=min 0.5×0+2+4+f3(1)=min 6+12 =17.5 0.5×0+2+5+f3(2) 7+11.5 u2(0)=3 0.5×1+2+2+f3(0) 4.5+12.5 f2(1)=min 0.5×1+2+3+f3(1)=min 5.5+12 =16.5 0.5×1+2+4+f3(2) 6.5+11.5 0.5×1+2+5+f3(3) 7.5+9 u2(1)=5 0.5×2+2+1+f3(0) 4+12.5 0.5×2+2+2+f3(1) 5+12 f2(2)=min 0.5×2+2+3+f3(2)=min 6+11.5 =16 0.5×2+2+4+f3(3) 7+9 0.5×2+2+5+f3(4) 8+9 u2(2)=4

注意:3-x2≤u2≤min{5,7-x2},X2+u2-d2-x3 d2=3 0.5×3+0+5(0) 1.5+12.5 0.5×3+2+1+5(1) 4.5+12 龙(3)=min{0.5×3+2+2+6 (2) =min 5.5+11.5=14 0.5×3+2+3+5(3) 6.5+9 0.5×3+2+4+5(4) 7.5+9 2(3)=0 0.5×4+0+5(1) 2+12 五(4)=minJ0.5×4+2+1+5(2) =min 5+11.5=14 0.5×4+2+2+5(3〉 6+9 0.5×4+2+3+5(4) 7+9 2(4)=0 k=1X1=1 注意:0≤X1+u1-d1=X2≤4,而d1=2,.1≤u1≤5 于是有: 0.5×1+2+1+5(0) 3.5+17.5 0.5×1+2+2+5(1) 4.5+16.5 f(1)=min{0.5×1+2+3+5(2)=min 5.5+16=20.5 0.5×1+2+4+f5 (3) 6.5+14 0.5×1+2+5+5(4) 7.5+14 u1(1)=4 至此,已算得本问题1~4期最小总费用为20.5千元
注意:3-x2≤u2≤min{5,7-x2} ,x2+u2-d2=x3 d2=3 0.5×3+0+f3(0) 1.5+12.5 0.5×3+2+1+f3(1) 4.5+12 f2(3)=min 0.5×3+2+2+f3(2)=min 5.5+11.5 =14 0.5×3+2+3+f3(3) 6.5+9 0.5×3+2+4+f3(4) 7.5+9 u2(3)=0 0.5×4+0+f3(1) 2+12 f2(4)=min 0.5×4+2+1+f3(2)=min 5+11.5 =14 0.5×4+2+2+f3(3) 6+9 0.5×4+2+3+f3(4) 7+9 u2(4)=0 k=1 x1 =1 注意:0≤x1+u1-d1=x2≤4,而d1=2, ∴1≤u1≤5 , 于是有: 0.5×1+2+1+f2(0) 3.5+17.5 0.5×1+2+2+f2(1) 4.5+16.5 f1(1)=min 0.5×1+2+3+f2(2)=min 5.5+16 =20.5 0.5×1+2+4+f2(3) 6.5+14 0.5×1+2+5+f2(4) 7.5+14 u1(1)=4 至此,已算得本问题1~4期最小总费用为20.5千元
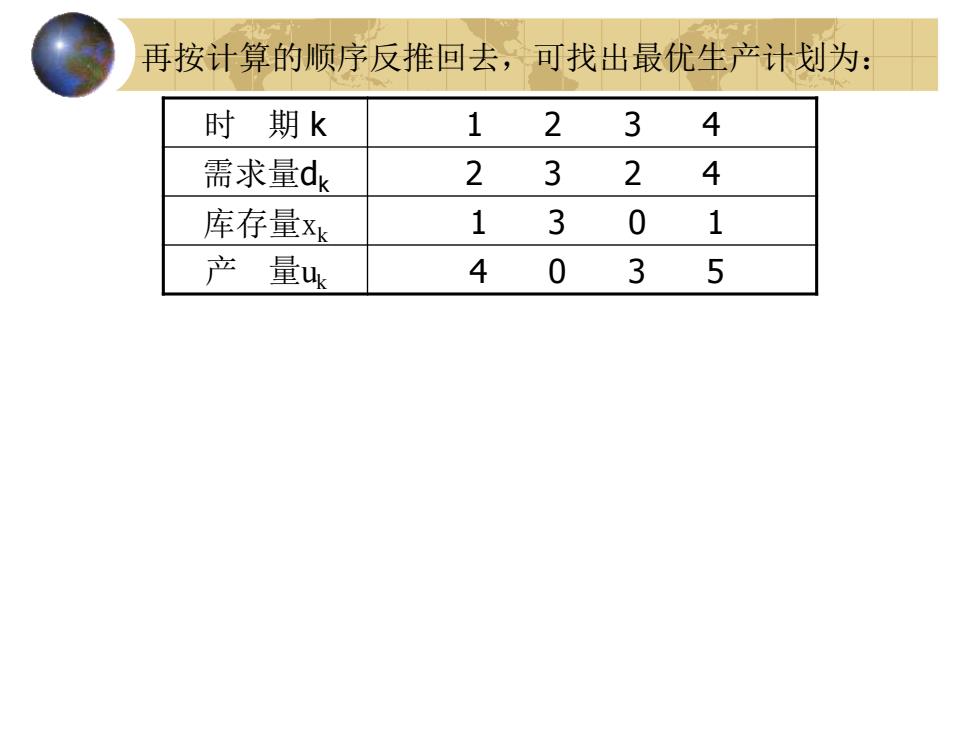
再按计算的顺序反推回去,可找出最优生产计划为: 时期k 1 2 3 4 需求量dk 2 3 2 4 库存量x 13 01 产量u 4 035
再按计算的顺序反推回去,可找出最优生产计划为: 时 期 k 1 2 3 4 需求量dk 2 3 2 4 库存量xk 1 3 0 1 产 量uk 4 0 3 5

运筹学 第六章动态规划应用举例 §2生产与存贮问题(续)
运 筹 学 第六章 动态规划应用举例 §2 生产与存贮问题(续)
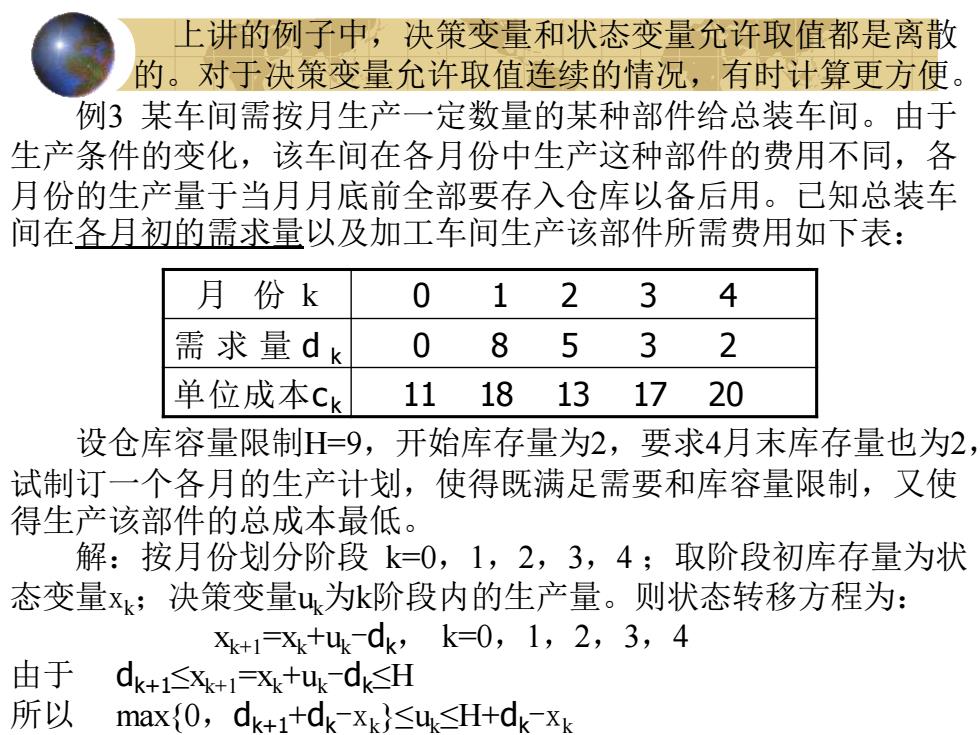
上讲的例子中,决策变量和状态变量允许取值都是离散 的。对于决策变量允许取值连续的情况,有时计算更方便。 例3某车间需按月生产一定数量的某种部件给总装车间。由于 生产条件的变化,该车间在各月份中生产这种部件的费用不同,各 月份的生产量于当月月底前全部要存入仓库以备后用。已知总装车 间在各月初的需求量以及加工车间生产该部件所需费用如下表: 月份k 需求量dk 0 8 5 3 2 单位成本Ck 1118 131720 设仓库容量限制H=9,开始库存量为2,要求4月末库存量也为2 试制订一个各月的生产计划,使得既满足需要和库容量限制,又使 得生产该部件的总成本最低。 解:按月份划分阶段k=0,1,2,3,4;取阶段初库存量为状 态变量xk;决策变量u为k阶段内的生产量。则状态转移方程为: Xk+1=X+udk,k=0,1,2,3,4 由于 dk+1≤Xk+1=X+ukdk≤H 所以 max{0,dk+1+dk-X}≤uk≤H+dk-xk
上讲的例子中,决策变量和状态变量允许取值都是离散 的。对于决策变量允许取值连续的情况,有时计算更方便。 例3 某车间需按月生产一定数量的某种部件给总装车间。由于 生产条件的变化,该车间在各月份中生产这种部件的费用不同,各 月份的生产量于当月月底前全部要存入仓库以备后用。已知总装车 间在各月初的需求量以及加工车间生产该部件所需费用如下表: 月 份 k 0 1 2 3 4 需求量 d k 0 8 5 3 2 单位成本c k 11 18 13 17 20 设仓库容量限制H=9,开始库存量为2,要求4月末库存量也为2, 试制订一个各月的生产计划,使得既满足需要和库容量限制,又使 得生产该部件的总成本最低。 解:按月份划分阶段 k=0,1,2,3,4 ;取阶段初库存量为状 态变量xk;决策变量uk为k阶段内的生产量。则状态转移方程为: xk+1=xk+uk-dk, k=0,1,2,3,4 由于 dk+1≤xk+1=xk+uk-dk≤H 所以 max{0,dk+1+dk-xk}≤uk≤H+dk-xk

记(x)为第k阶段至第4阶段末最小总费用,则动态规 划基本方程为: f厂职cu+fK+wd 方(x5)=0 k=4,3,2,1,0 k=4因为要求4月末库存量为2,即x4+u4d4=2,而d4=2,所以, u4=4-x,斤(x4)=C4u4-20(4-X4)=80-20x4, k=3注意:4-x4=420,.x≤4,又x4-X3+u3d3≥d4,而d3=3, ∴.5-x3≤3≤7-x3 f)u+f7u+80-20x+-3 >3u+140-20x=-37-x,+140-20x=119-17x, 3=7-X3 k=2注意:u3=7-x≥0,.X3≤7,又X3=X2+u2d2≥d3,而d2=5, ∴.8-X2≤u2≤12-x2 f,片c.u.+fkm13u+119-17:+w-列 .44+204-17x,F-412-x,+204-17x,=156-13x
记fk(xk)为第k阶段至第4阶段末最小总费用,则动态规 划基本方程为: ( ) = + + + − k u D f k xk min ckuk f k 1 xk uk d k K f5(x5)=0 k=4,3,2,1,0 k=4 因为要求4月末库存量为2,即x4+u4-d4=2,而d4=2,所以, u4=4-x4 ,f4(x4)=c4u4=20(4-x4)=80-20x4, k=3 注意:4-x4=u4≥0,∴x4≤4,又x4 =x3+u3-d3≥d4,而d3=3, ∴5-x3≤u3≤7-x3 ( ) ( ) = + = + − + − − − − − f x min c u f x min 17u3 80 20 x3 u3 3 7 3 3 4 4 7 3 3 5 x3 u3 x3 5 x3 u3 x3 3 3 3 3 3 7 min 3u 140 20x 37 x 140 20x 119 17x 5 x3 u3 x3 = − + − =− − + − = − − − u3=7-x3 k=2 注意:u3=7-x3≥0,∴x3≤7,又x3 =x2+u2-d2≥d3,而d2=5, ∴8-x2≤u2≤12-x2 ( ) ( ) = + = + − + − − − − − f x min c u f x min 13u2 119 17 x2 u2 5 12 2 2 3 3 12 2 2 8 x2 u2 x2 8 x2 u2 x2 2 2 2 2 2 12 min 4 204 17 4 12 204 17 156 13 8 2 2 2 u x x x x x u x = − + − =− − + − = − − −