
§2表上作业法 2.2最优性检验 在求出间题的一个可行方案后, 就应该判断这个方案是不是最 优的。为了进行最优性判别,下面先给出检验数的概念。 对于空格(,),假定给它一个单位运量,调整其他有关数字 格运量,则称这一系列变化导致的总运费变化值为该空格的检验数 记作σ。当一个空格的检验数大于零,说明将该空格变为数字格会 引起总运量费增加,反之,如果该空格检验数为负值,说明将该空 格变为数字格会使总运费降低。因此有以下判别准则: 定理:如果一个可行方案的所有空格检验数都大于或等于零, 则该方案是最优方案。 事实上,按单纯形法,运输问题用非基变量表示的目标函数为 Z=CBb+∑oX,,显然,单纯形法中的检验数与上述定义的空格 检验数是一致的。而运输问题的目标函数是求最小值,自然有上述 定理成立。 对于一个可行方案,只要求出所有空格的检验数,就可以判 别该方案是否为最优方案,那么如何求得一个空格的检验数呢? 下面给出两种计算检验数的方法
§2 表上作业法 2.2 最优性检验 在求出问题的一个可行方案后,就应该判断这个方案是不是最 优的。为了进行最优性判别,下面先给出检验数的概念。 对于空格(i,j),假定给它一个单位运量,调整其他有关数字 格运量,则称这一系列变化导致的总运费变化值为该空格的检验数, 记作σij。当一个空格的检验数大于零,说明将该空格变为数字格会 引起总运量费增加,反之,如果该空格检验数为负值,说明将该空 格变为数字格会使总运费降低。因此有以下判别准则: 定理:如果一个可行方案的所有空格检验数都大于或等于零, 则该方案是最优方案。 事实上,按单纯形法,运输问题用非基变量表示的目标函数为 Z=CBB-1b+ Σσijxij ,显然,单纯形法中的检验数与上述定义的空格 检验数是一致的。而运输问题的目标函数是求最小值,自然有上述 定理成立。CBB -1b 对于一个可行方案,只要求出所有空格的检验数,就可以判 别该方案是否为最优方案,那么如何求得一个空格的检验数呢? 下面给出两种计算检验数的方法
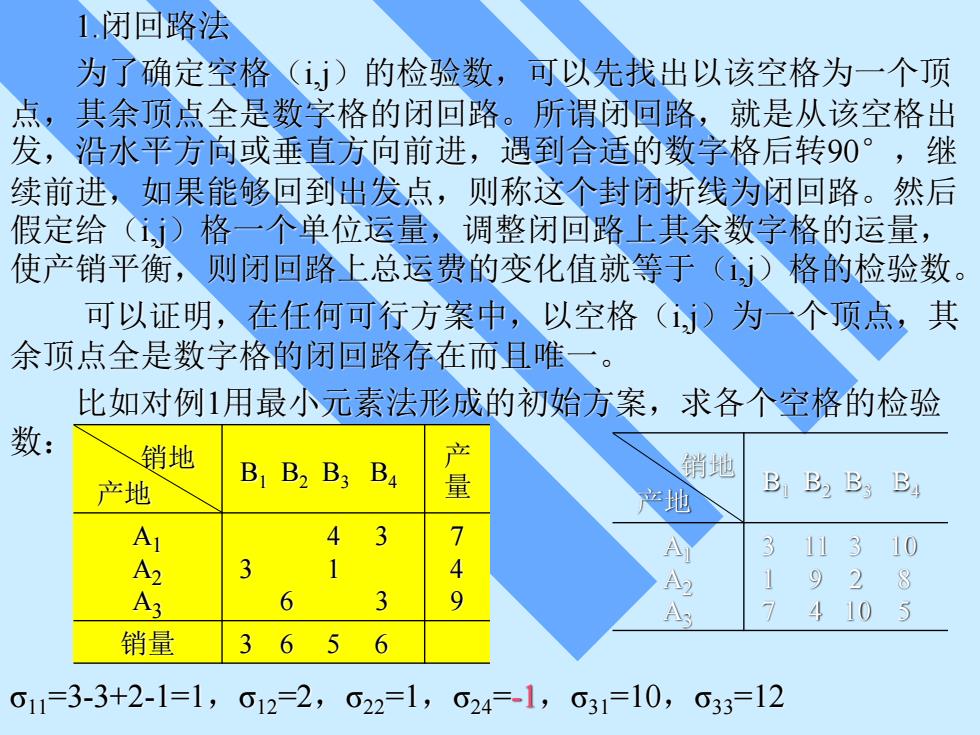
1,闭回路法 为了确定空格(j)的检验数,可以先找出以该空格为一个顶 点,其余顶点全是数字格的闭回路。所谓闭回路,就是从该空格出 发,沿水平方向或垂直方向前进,遇到合适的数字格后转90°,继 续前进,如果能够回到出发点,则称这个封闭折线为闭回路。然后 假定给()格一个单位运量,调整闭回路上其余数字格的运量, 使产销平衡,则闭回路上总运费的变化值就等于j)格的检验数。 可以证明,在任何可行方案中,以空格()为一个项点,其 余顶点全是数字格的闭回路存在而且唯一。 比如对例1用最小元素法形成的初始方案,求各个空格的检验 数: 销地 销地 产地 B B2 B3 B4 量 地 BB,B:B A 4 A可 3 11310 928 6 A 4105 销量 3 6 6 011-3-3+2-1=1,012=2,022=1,024=-1,031=10,033=12
1.闭回路法 为了确定空格(i,j)的检验数,可以先找出以该空格为一个顶 点,其余顶点全是数字格的闭回路。所谓闭回路,就是从该空格出 发,沿水平方向或垂直方向前进,遇到合适的数字格后转90°,继 续前进,如果能够回到出发点,则称这个封闭折线为闭回路。然后 假定给(i,j)格一个单位运量,调整闭回路上其余数字格的运量, 使产销平衡,则闭回路上总运费的变化值就等于(i,j)格的检验数。 可以证明,在任何可行方案中,以空格(i,j)为一个顶点,其 余顶点全是数字格的闭回路存在而且唯一。 比如对例1用最小元素法形成的初始方案,求各个空格的检验 数: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 4 3 3 1 6 3 7 4 9 销量 3 6 5 6 销地 产地 B1 B2 B3 B4 A1 A2 A3 3 11 3 10 1 9 2 8 7 4 10 5 σ11=3-3+2-1=1,σ12=2,σ22=1,σ24 =-1,σ31=10,σ33=12

2.位势法 用闭回路法求检验数时,需要找出每个空格所在的闭回路,当 产销点很多时,计算量非常大。下面介绍一种求检验数的简便方 法一位势法。 设Y=(u1,u2un,V1,V2Vn)是运输问题的mtn个约束条件对应 的对偶变量,决策变量x对应的列向量Pe+en?对于一个基可 行解,由单纯形法得知所有基变量x1)(数字格)的检验数等于0, 即0=Ch-CBB-Pij-C,-YPC;(utv),所以由m+n-1个数字格对 应的C(u:+v)及u0即可确定所有u,V的值。 称u1,2u,V1,V2Vn分别为产销平衡表各行与各列的位势。 因为非基变量(空格)检验数Ci-YP=C(u),所以, 只要计算出所有位势值,就能求出各空格的检验数。 这些计算可以直接在表格中进行。以例1的初始方案为例:
2.位势法 用闭回路法求检验数时,需要找出每个空格所在的闭回路,当 产销点很多时,计算量非常大。 下面介绍一种求检验数的简便方 法——位势法。 设Y=(u1,u2…um,v1,v2…vn)是运输问题的m+n个约束条件对应 的对偶变量,决策变量xij对应的列向量Pij=ei+em+j,对于一个基可 行解,由单纯形法得知所有基变量xij(数字格)的检验数等于0, 即0=Cij-CBB-1Pij =Cij-YPij= Cij-(ui+vj),所以由m+n-1个数字格对 应的Cij =(ui+vj)及u1=0即可确定所有ui,vj的值。 称u1,u2…um,v1,v2…vn分别为产销平衡表各行与各列的位势。 因为非基变量(空格)检验数σij =Cij-YPij= Cij-(ui+vj),所以, 只要计算出所有位势值,就能求出各空格的检验数。 这些计算可以直接在表格中进行。以例1的初始方案为例:

初始方案表: 单位运价表 销地 B B2 B3 B4 销地 产地 产地 B B2 B3 B4 (2)4 0 3 A 31) 11310 1 -1 A (10)612)3 -5 A 928 A3 4105 Vj 293 10 先由mtn-l个数字格对应的C)(u:tv;),确定所有u,v的值。 令u1=0,由(1,3)处数字格运价3=u13,可得v3=3,类似可求得 其它C(u+v;)的值,见方案表中红色数字。 再按公式o,C(u:)计算空格的检验数,结果见方案表中 带括号的红色数字。 可以验证,按位势法与按闭回路法算得的检验数完全一致。 事实上,若设空格(ij)所在闭回路上数字格依次位x1,x11, xi1j2,Xi2j2…X1sj,则按闭回路可以算得: o-CCij1tCi1j1-Ci12+Ci2j2…-Cis=Cf(u1tVj1)+(u1tvj1) (ui1+Vj2)+(ui2tvj2).-(uis+Vj)=C(u+Vj)
销地 产地 B1 B2 B3 B4 ui A1 A2 A3 4 3 3 1 6 3 vj 销地 产地 B1 B2 B3 B4 A1 A2 A3 3 11 3 10 1 9 2 8 7 4 10 5 初始方案表: 单位运价表 先由m+n-1个数字格对应的Cij =(ui+vj),确定所有ui,vj的值。 令u1=0,由(1,3)处数字格运价3= u1+v3,可得v3=3,类似可求得 其它Cij =(ui+vj)的值,见方案表中红色数字。 0 3 10 -1 -5 2 9 再按公式σij =Cij-(ui+vj)计算空格的检验数,结果见方案表中 带括号的红色数字。 (1)(2) (10) (1) (-1) (12) 可以验证,按位势法与按闭回路法算得的检验数完全一致。 事实上,若设空格(i,j)所在闭回路上数字格依次位xij1, xi1j1, xi1j2, xi2j2 …xisj,则按闭回路可以算得: σij=Cij-Cij1+Ci1j1-Ci1j2+Ci2j2 …-Cisj =Cij-(ui+vj1)+(ui1+vj1)- (ui1+vj2)+(ui2+vj2)…-(uis+vj)=Cij-(ui+vj)

2.3方案的调整一闭回路法 当空格的检验数出现负值时,说明当前平衡表给出的调运方案 不是最优的,可以进行调整,使总运输费用减少。调整方法如下: 1°为了使方案有较大改进,先确定最小检验数,即 mino<0)=OLK 2°找出以空格(L,K)为一个顶点,其余顶点全是数字格的 闭回路,规定空格(L,K)为闭回路的第一个顶点,闭回路上其它 顶点依次为第二个顶点,第三个项点,…(顺时针或逆时针均可)。 取闭回路上偶数序号顶点的最小运量为调整量0。 3°闭回路上偶数序号顶点的运量均减9,奇数序号顶点的运 量均加0,不在闭回路上的运量不变。调整中,如果偶数序号顶点 中仅有一个数字格的运量等于0,则调整后,该格变为空格;如果 偶数序号顶点中有两个以上数字格运量等于调整量0,则调整后, 仅让其中一个数字格变为空格,其它调整后要记“0”,表示该格 为数字格。经这样调整,就可以得到一个含有m+n-1个数字格的新 的调运方案。 如例1的初始方案经检验,存在一个负检验数σ24=-1,所以
2.3 方案的调整——闭回路法 当空格的检验数出现负值时,说明当前平衡表给出的调运方案 不是最优的,可以进行调整,使总运输费用减少。调整方法如下: 1°为了使方案有较大改进,先确定最小检验数,即 min{σij│σij<0}= σLK 2°找出以空格(L,K)为一个顶点,其余顶点全是数字格的 闭回路,规定空格(L,K)为闭回路的第一个顶点,闭回路上其它 顶点依次为第二个顶点,第三个顶点,…(顺时针或逆时针均可)。 取闭回路上偶数序号顶点的最小运量为调整量θ。 3°闭回路上偶数序号顶点的运量均减θ,奇数序号顶点的运 量均加θ,不在闭回路上的运量不变。调整中,如果偶数序号顶点 中仅有一个数字格的运量等于θ,则调整后,该格变为空格;如果 偶数序号顶点中有两个以上数字格运量等于调整量θ,则调整后, 仅让其中一个数字格变为空格,其它调整后要记“0”,表示该格 为数字格。经这样调整,就可以得到一个含有m+n-1个数字格的新 的调运方案。 如例1 的初始方案经检验,存在一个负检验数σ24 =-1,所以

该方案不是最优方案,在平衡表中找出闭回路下表所示: 销地 BI B2 B3 B4 销地 产地 量 产地 B B2 B3 B4 AN生 7 3 11310 9 M 92 8 A3 410、5 销量 3 6 6 调整量0=1,调整后得新方案如下表: 对新方案的检验结果如下表: 销地 B B2 B3 B4 产地 量 销地 B B, B3 B A 5 2 7 产地 (0) (2) 5 2 3 9 M (2)(1)1 销量 6 5 A3 (9) 6 (12)3 V 3 9 3 10 表中所有检验数均非负,故调整后的新方案已是最优方案。最小总 运费为:5×3+2×10+3×1+1×8+6X4+3×5=85 (元)
该方案不是最优方案,在平衡表中找出闭回路下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 4 3 3 1 6 3 7 4 9 销量 3 6 5 6 调整量θ=1,调整后得新方案如下表: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 5 2 3 1 6 3 7 4 9 销量 3 6 5 6 销地 产地 B1 B2 B3 B4 A1 A2 A3 3 11 3 10 1 9 2 8 7 4 10 5 对新方案的检验结果如下表: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 5 2 3 1 6 3 vj 0 10 -2 -5 3 9 3 (0)(2) (2)(1) (9) (12) 表中所有检验数均非负,故调整后的新方案已是最优方案。最小总 运费为:5×3+2×10+3×1+1×8+6×4+3×5=85(元)