
第三章运输问题 前两章讨论了一般线性规划的解法,但在实际工作中,往往 碰到有些线性规划问题,它们的约束方程组的系数矩阵具有很特 殊的结构,这就有可能找到比单纯形法更为简便的求解方法。本 章讨论的运输问题就是这样一类特殊的线性规划问题。 §1运输问题 在经济活动中,经常碰到大宗物资的调运问题。如煤、钢铁、 木材、粮食等物资,在全国有若干生产基地,根据已有的交通网, 制定调运方案,将这些物资运到各消费地点,而总运费最省。 这类问题的一般提法是:设某物资有m个产地A1,A2,,Am, 其产量分别为a1,a2,,am,有n个销地B1,B2,,Bn,其销量分别 是b1,b2,,b,己知产地A到销地B的单位运费是Ci,这些数据可用 产销平衡表和单位运价表表示如下:
第三章 运输问题 前两章讨论了一般线性规划的解法,但在实际工作中,往往 碰到有些线性规划问题,它们的约束方程组的系数矩阵具有很特 殊的结构,这就有可能找到比单纯形法更为简便的求解方法。本 章讨论的运输问题就是这样一类特殊的线性规划问题。 §1 运输问题 在经济活动中,经常碰到大宗物资的调运问题。如煤、钢铁、 木材、粮食等物资,在全国有若干生产基地,根据已有的交通网, 制定调运方案,将这些物资运到各消费地点,而总运费最省。 这类问题的一般提法是:设某物资有m个产地A1,A2,…,Am, 其产量分别为a1,a2,…,am,有n个销地B1,B2,…,Bn,其销量分别 是b1,b2,…,bn,已知产地Ai到销地Bj的单位运费是Cij,这些数据可用 产销平衡表和单位运价表表示如下:
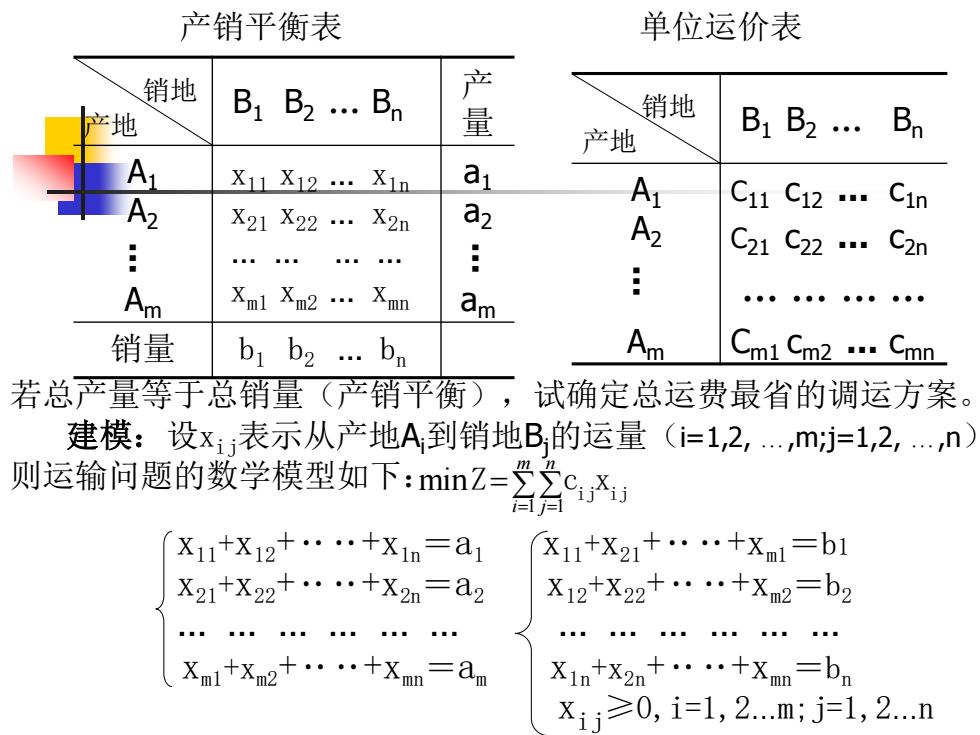
产销平衡表 单位运价表 销地 产 销地 产地 B1 B2...Bn 量 产地 B1B2…Bn A X11X12…X1n ai 2 a2 A C11C12… Cin X21X22… X2n 2 C21C22"C2n 。 Am Xml Xma2…Xmm am 销量 bi b2...bn Cmi Cm2 ....Cmn 若总产量等于总销量(产销平衡),试确定总运费最省的调运方案。 建模:设x表示从产地A到销地B,的运量(i=1,2,…,mj=1,2,n) 则运输闲题的数学模型如下:mnZ- X11+X12+……+X1n=a1 X11+X21+…+xm1=b1 X21+X22+……+X2n=a2 X12+X22+·…+xm2=b2 Xn1X2十……+Xmn=a X1n+x2n+……+Xm=bn xi≥0,i-1,2..m;j=1,2.n
销地 产地 B1 B2 … Bn 产 量 A1 A2 a1 … a … 2 Am am 销量 b1 b2 … bn 销地 产地 B1 B2 … Bn A1 A2 C11 c12 … c1n … C21 c22 … c2n … … … … Am Cm1 cm2 … cmn 产销平衡表 单位运价表 x11 x12 … x1n x21 x22 … x2n … … … … xm1 xm2 … xmn 若总产量等于总销量(产销平衡),试确定总运费最省的调运方案。 建模:设xij表示从产地Ai到销地Bj的运量(i=1,2, …,m;j=1,2, …,n) 则运输问题的数学模型如下: = = = m i n 1 j 1 min ij ij Z c x x11+x12+‥‥+x1n =a1 x11+x21+‥‥+xm1 =b1 x21+x22+‥‥+x2n =a2 x12+x22+‥‥+xm2 =b2 … … … … … … … … … … … … xm1+xm2+‥‥+xmn =am x1n+x2n+‥‥+xmn =bn xij≥0,i=1,2…m;j=1,2…n
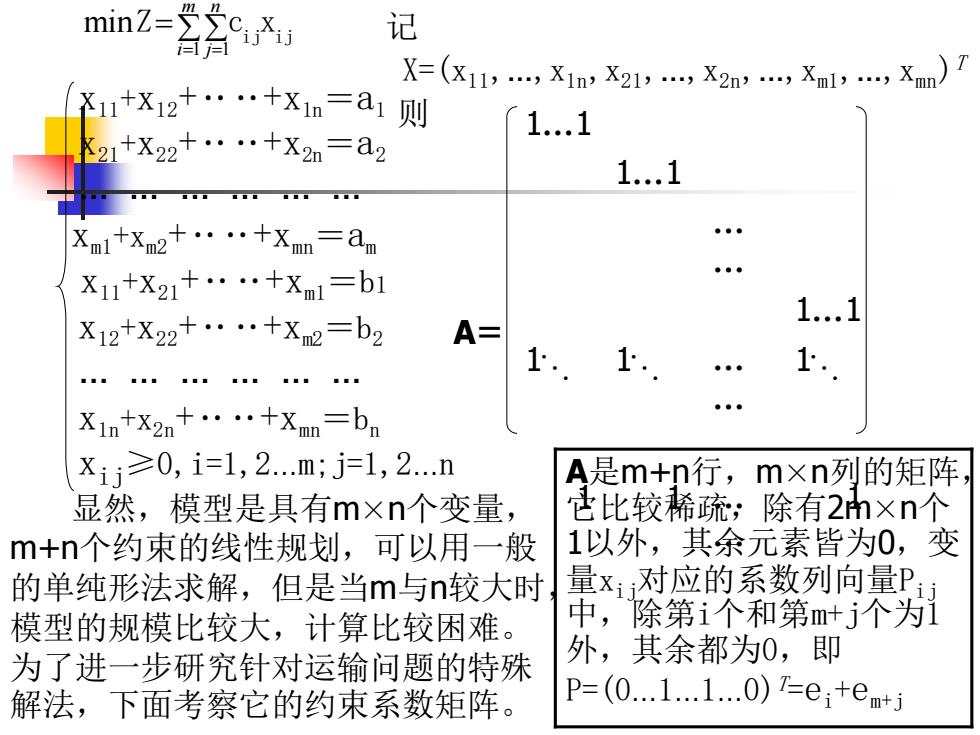
minZ= 记 (X11,,X1nX21,,X2n3,Xa1,,Xmn) 1+X12十……+X1n=a1则 1..1 +X22+……+X2n=a2 1..1 1■■ Xml+Xm2+…+Xmm=an X11+X21+……+Xm1=b1 X12+X22+……+X2=b2 1..1 A= 1. 1 X1ntx2n+…+Xnm=bn x1j≥0,i-1,2.m;j=1,2n A是m+n行,m×n列的矩阵 显然,模型是具有m×n个变量, 色比较稀疏;除有2h×n个 m+n个约束的线性规划,可以用一般 1以外,其余元素皆为0,变 的单纯形法求解,但是当m与n较大时量x对应的系数列向量P 模型的规模比较大,计算比较困难。 中,除第i个和第m+j个为1 为了进一步研究针对运输问题的特殊 外,其余都为0,即 解法,下面考察它的约束系数矩阵。 P=(01.1.0)=e+em+j
= = = m i n 1 j 1 min ij ij Z c x x11+x12+‥‥+x1n =a1 x21+x22+‥‥+x2n =a2 … … … … … … xm1+xm2+‥‥+xmn =am x11+x21+‥‥+xm1 =b1 x12+x22+‥‥+xm2 =b2 … … … … … … x1n+x2n+‥‥+xmn =bn xij≥0,i=1,2…m;j=1,2…n 显然,模型是具有m×n个变量, m+n个约束的线性规划,可以用一般 的单纯形法求解,但是当m与n较大时, 模型的规模比较大,计算比较困难。 为了进一步研究针对运输问题的特殊 解法,下面考察它的约束系数矩阵。 记 X=(x11,…,x1n,x21,…,x2n,…,xm1,…,xmn) T 则 A= 1…1 1…1 … … 1…1 1 1 … … 1 1 1 … … 1 A是m+n行,m×n列的矩阵, 它比较稀疏,除有2m×n个 1以外,其余元素皆为0,变 量xij对应的系数列向量Pij 中,除第i个和第m+j个为1 外,其余都为0,即 P=(0…1…1…0)T =ei+em+j
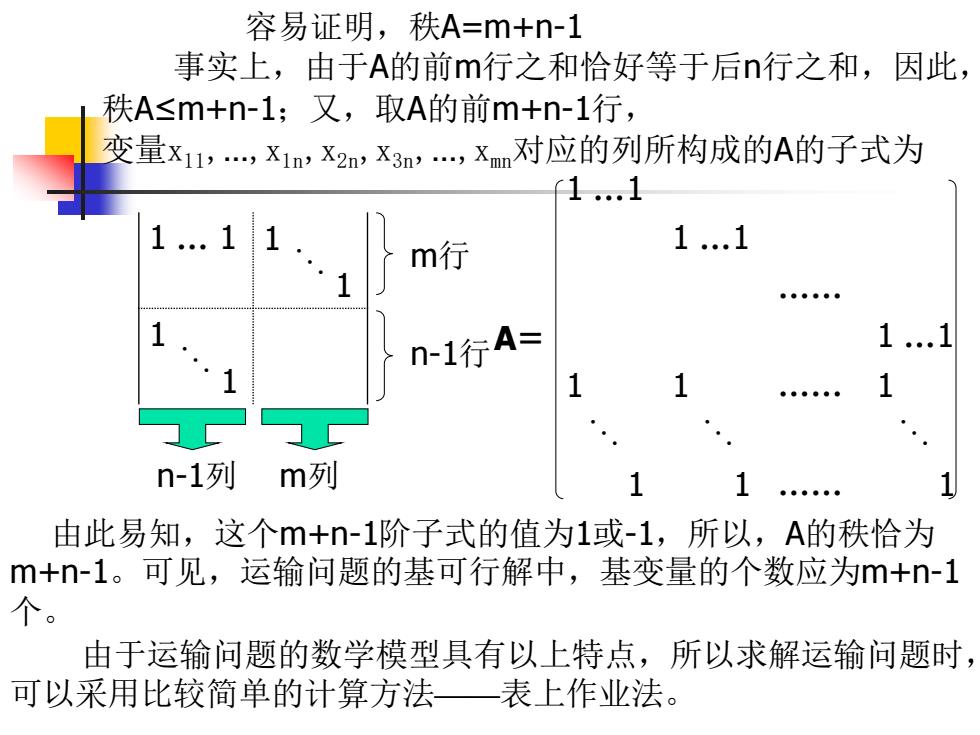
容易证明,秩A=m+n-1 事实上,由于A的前m行之和恰好等于后n行之和,因此, 秩A≤m+n-1;又,取A的前m+n-1行, 变量X1,,X1,X2n,X3,,Xm对应的列所构成的A的子式为 1..1 1.1 m行 1..1 n-1行A= 1..1 1 n-1列 m列 1 由此易知,这个m+n-1阶子式的值为1或-1,所以,A的秩恰为 m+n-1。可见,运输问题的基可行解中,基变量的个数应为m+n-1 个。 由于运输问题的数学模型具有以上特点,所以求解运输问题时, 可以采用比较简单的计算方法—表上作业法
容易证明,秩A=m+n-1 事实上,由于A的前m行之和恰好等于后n行之和,因此, 秩A≤m+n-1;又,取A的前m+n-1行, 变量x11,…,x1n,x2n,x3n,…,xmn对应的列所构成的A的子式为 1 … 1 1 1 1 1 m行 n-1行 n-1列 m列 由此易知,这个m+n-1阶子式的值为1或-1,所以,A的秩恰为 m+n-1。可见,运输问题的基可行解中,基变量的个数应为m+n-1 个。 由于运输问题的数学模型具有以上特点,所以求解运输问题时, 可以采用比较简单的计算方法——表上作业法。 A= 1 …1 1 …1 …… 1 …1 1 1 …… 1 1 1 …… 1

§2表上作业法 表上作业法的思想和单纯形法类似,即首先确定一个初 始方案,也就是找出一个基可行解,然后根据判别准则来检 查这个初始方案是不是最优的,如果不是最优的,那么对该 方案进行调整,直至求出最优方案止。下面介绍它的计算步 骤。 2.1确定初始调运方案 确定初始调运方案的方法很多,我们介绍两种:最小元素法和 西北角法。 1.最小元素法 这个方法的基本思想是就近供应,即从运价表中最小运价开始 确定调运量,然后次小,一直到给出初始调运方案为止。具体操作 方法如下: 1°找出运价表中最小元素CuK,确定XK=min{aL,bk},若xK=aL, 则令bk'=bkxK,划掉运价表的第L行;反之,若xLK=bk,则令 aL'=aLXK,划掉运价表的第K列。 2°在运价表剩余元素中重复1°,直至运价表中元素全被划掉止
§2 表上作业法 表上作业法的思想和单纯形法类似,即首先确定一个初 始方案,也就是找出一个基可行解,然后根据判别准则来检 查这个初始方案是不是最优的,如果不是最优的,那么对该 方案进行调整,直至求出最优方案止。下面介绍它的计算步 骤。 2.1 确定初始调运方案 确定初始调运方案的方法很多,我们介绍两种:最小元素法和 西北角法。 1.最小元素法 这个方法的基本思想是就近供应,即从运价表中最小运价开始 确定调运量,然后次小,一直到给出初始调运方案为止。具体操作 方法如下: 1°找出运价表中最小元素CLK,确定xLK=min{aL,bk},若xLK = aL, 则令bk ′=bk-xLK,划掉运价表的第L行;反之,若xLK= bk ,则令 aL ′=aL-xLK,划掉运价表的第K列。 2°在运价表剩余元素中重复1°,直至运价表中元素全被划掉止
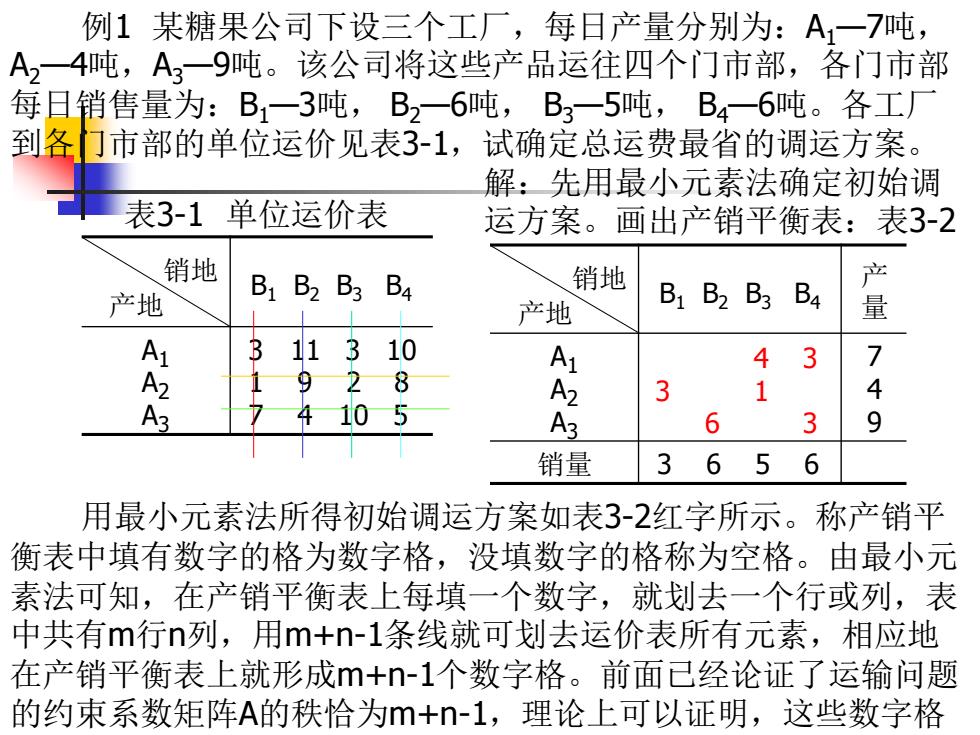
例1某糖果公司下设三个工厂,每日产量分别为:A一7吨, A,一吨,A?一9吨。该公司将这些产品运往四个门市部,各门市部 每日销售量为:B1一3吨,B2一6吨,B3一5吨,B4一6吨。各工 到各门市部的单位运价见表3-1,试确定总运费最省的调运方案。 解:先用最小元素法确定初始调 表3-1单位运价表 运方案。画出产销平衡表:表3-2 销地 B1 B2 B3 B4 销地 产 产地 产地 B1 B2 B3 B4 量 11 3 10 4 7 A2 8 A2 3 4 10 6 9 销量 3 6 5 6 用最小元素法所得初始调运方案如表3-2红字所示。称产销平 衡表中填有数字的格为数字格,没填数字的格称为空格。由最小元 素法可知,在产销平衡表上每填一个数字,就划去一个行或列,表 中共有m行n列,用m+n-1条线就可划去运价表所有元素,相应地 在产销平衡表上就形成m+-1个数字格。前面已经论证了运输问题 的约束系数矩阵A的秩恰为m+n-1,理论上可以证明,这些数字格
例1 某糖果公司下设三个工厂,每日产量分别为:A1—7吨, A2—4吨,A3—9吨。该公司将这些产品运往四个门市部,各门市部 每日销售量为:B1—3吨, B2—6吨, B3—5吨, B4—6吨。各工厂 到各门市部的单位运价见表3-1,试确定总运费最省的调运方案。 表3-1 单位运价表 销地 产地 B1 B2 B3 B4 A1 A2 A3 3 11 3 10 1 9 2 8 7 4 10 5 解:先用最小元素法确定初始调 运方案。画出产销平衡表:表3-2 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 7 4 9 销量 3 6 5 6 3 1 4 6 3 3 用最小元素法所得初始调运方案如表3-2红字所示。称产销平 衡表中填有数字的格为数字格,没填数字的格称为空格。由最小元 素法可知,在产销平衡表上每填一个数字,就划去一个行或列,表 中共有m行n列,用m+n-1条线就可划去运价表所有元素,相应地 在产销平衡表上就形成m+n-1个数字格。前面已经论证了运输问题 的约束系数矩阵A的秩恰为m+n-1,理论上可以证明,这些数字格 所

所对应的变量相当于基变量,而空格对应的变量相当于非基变量, 用最小元素法得到的初始调运方案构成一个基可行解。 特别要注意的是:当最小运价Ck对应的产量a与销量b, 相等时,在产销平衡表填上XK=a时,产销平衡表的第L 行和第K列同时得到满足,为了保证基变量个数为m+n-1 个,除了在表上填xK=a外,必须在表的第L行或第K列 某空格(相应运价未被划掉)处填一个“0”,然后同时 划去运价表的第L行与第K列。该“0”看作是数字格,即 对应的基变量取0值
所对应的变量相当于基变量,而空格对应的变量相当于非基变量, 用最小元素法得到的初始调运方案构成一个基可行解。 特别要注意的是:当最小运价CLK对应的产量 aL与销量bk 相等时,在产销平衡表填上xLK = aL时,产销平衡表的第L 行和第K列同时得到满足,为了保证基变量个数为m+n-1 个,除了在表上填xLK = aL外,必须在表的第L行或第K列 某空格(相应运价未被划掉)处填一个“0”,然后同时 划去运价表的第L行与第K列。该“0”看作是数字格,即 对应的基变量取0值

2.西北角法 西北角法的基本思想是给产销平衡表左上角的变量分配运输量, 以确定产销关系,依此类推,一直到给出初始可行方案为止。 求解步骤如下: 先决定产销平衡表左上角变量XK的值。令这个变量取尽可 能大的值,即xk=min{aL,bk},在这个变量对应的数字格填上变 量所取的值。 2°若xK=aL,则在第L行空格处打“×”,这些空格不再赋值: 若xK=bk,则在第K列空格处打“×”,这些空格不再赋值;若xK ==bk,则在行的空格处打“×”后,就不能在列的空格处打 “×”,反之,若在列的空格处打“×”,就不在行空格处打 “X” 3°对表上没有打“×”的地方重复1°,2°步,直到所有格 子都有标记止。 可以证明,用西北角法确定的初始方案是运输问题的一个初始基 可行解,它也恰好包含m+n-1个数字格
2.西北角法 西北角法的基本思想是给产销平衡表左上角的变量分配运输量, 以确定产销关系,依此类推,一直到给出初始可行方案为止。 求解步骤如下: 1°先决定产销平衡表左上角变量xLK 的值。令这个变量取尽可 能大的值,即xLK=min{aL,bk} ,在这个变量对应的数字格填上变 量所取的值。 2°若xLK = aL,则在第L行空格处打“×”,这些空格不再赋值; 若xLK =bk,则在第K列空格处打“×”,这些空格不再赋值;若xLK = aL=bk,则在行的空格处打“×”后,就不能在列的空格处打 “×”,反之,若在列的空格处打“×”,就不在行空格处打 “×” 。 3°对表上没有打“×”的地方重复1°,2°步,直到所有格 子都有标记止。 可以证明,用西北角法确定的初始方案是运输问题的一个初始基 可行解,它也恰好包含m+n-1个数字格
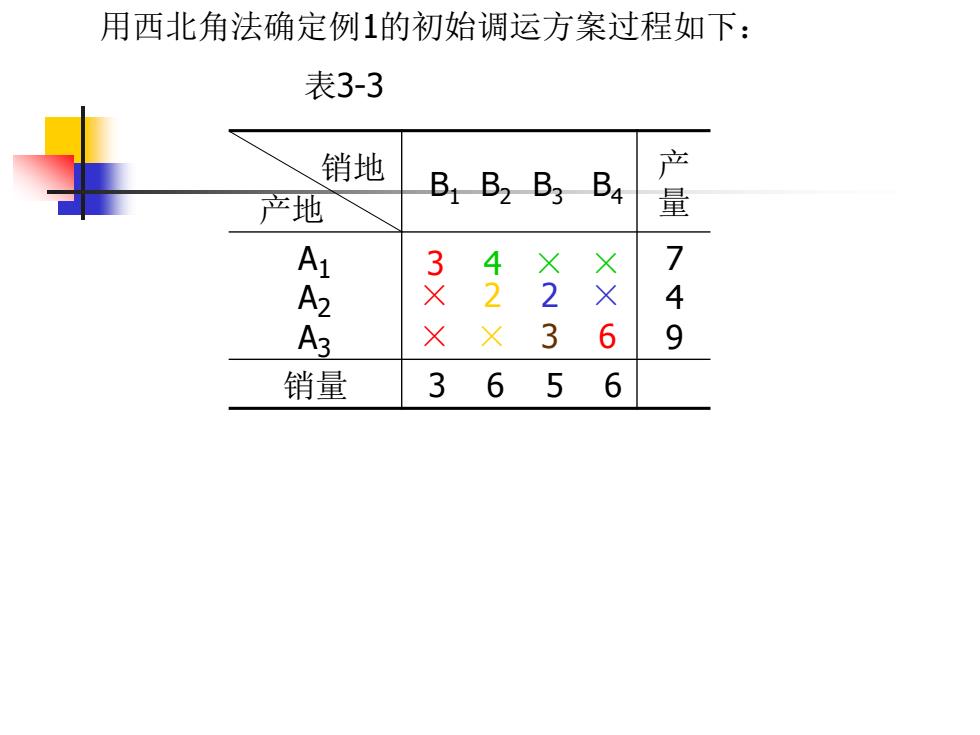
用西北角法确定例1的初始调运方案过程如下: 表3-3 销地 产 B B2 B3 B4 产地 量 A × 7 A2 3× 4 × X 3 6 9 销量 3 656
用西北角法确定例1的初始调运方案过程如下: 表3-3 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 7 4 9 销量 3 6 5 6 3 × × 4 × × 2 × 2 × 3 6