
§4复合系统工作可靠性问题 某种工作系统由个部件串联组成,称部件正常工作问 的概率为部件的可靠性,称整个系统正常工作的概率为系 统的可靠性。如图: 部件1 部件2 部件n 在这样的串联系统中,只要有一个部件失灵, 整个系令 统就不能正常工作。为了提高系统工作的可靠性,可以给 各部件设置备用件,并且设计备用件自动投入装置,一旦 部件损坏,则备用件自动投入运行。显然,部件的备用件 越多,部件的工作可靠性就越大,从而,整个系统的工作 可靠性也就越大。但是备用件多了,整个系统的成本、重 量、体积都相应增大。而系统所允许的总成本、总重量、 总体积往往都是有限的,因此,复合系统工作可靠性问题 主要讨论在上述限制条件下,如何选择各部件的备用件数 量,使系统的工作可靠性最大。下面我们先研究这类问题 的数学模型
§4 复合系统工作可靠性问题 某种工作系统由n个部件串联组成,称部件正常工作 的概率为部件的可靠性,称整个系统正常工作的概率为系 统的可靠性。如图: 部件1 部件2 部件n 在这样的串联系统中,只要有一个部件失灵,整个系 统就不能正常工作。为了提高系统工作的可靠性,可以给 各部件设置备用件,并且设计备用件自动投入装置,一旦 部件损坏,则备用件自动投入运行。显然,部件的备用件 越多,部件的工作可靠性就越大,从而,整个系统的工作 可靠性也就越大。但是备用件多了,整个系统的成本、重 量、体积都相应增大。而系统所允许的总成本、总重量、 总体积往往都是有限的,因此,复合系统工作可靠性问题 主要讨论在上述限制条件下,如何选择各部件的备用件数 量,使系统的工作可靠性最大。下面我们先研究这类问题 的数学模型

设部件i装有u个备用件时,它正常工作的概率为p(u) 因此整个系统正常工作的概率为: P=Ip(u) 设装部件i的一个备用件费用为c元, 要求总费用不超 过C元,则这个问题只有 一个约束条件,它的静态模型为: max P=IIp.(u) cusC 这是一个非线性规划问题。象资源分配问题一样,可 以用动态规划方法求解这类间题。不过与以前的资源分配 问题不同,本间题的总效果不是等于各阶段效果的和,而 是各阶段效果的乘积。下面构造它的动态规划模型: 以向各部件分配备用件的顺序为阶段k=1,2, 以k阶段初拥有的未分配的费用数x为状态变量;决策 变量u表示部件k拥有的元件数,则+1C 记(xk)为部件k至部件最大工作可靠性,则 人(xk)=maXp(u)人1(X+1) k=n,n-1,,2,1
设部件i 装有ui个备用件时,它正常工作的概率为pi(ui)。 因此整个系统正常工作的概率为: = ( ) = n i P pi ui 1 设装部件i 的一个备用件费用为ci元,要求总费用不超 过C元,则这个问题只有一个约束条件,它的静态模型为: ( ) cu C P p u i n i i n i i i = = = 1 1 max 这是一个非线性规划问题。象资源分配问题一样,可 以用动态规划方法求解这类问题。不过与以前的资源分配 问题不同,本问题的总效果不是等于各阶段效果的和,而 是各阶段效果的乘积。下面构造它的动态规划模型: 以向各部件分配备用件的顺序为阶段 k=1,2,…,n; 以k阶段初拥有的未分配的费用数xk为状态变量;决策 变量uk表示部件k拥有的元件数,则 xk+1=xk-ckuk 记fk(xk)为部件k至部件n最大工作可靠性,则 fk(xk)= max{pk (uk ) ·fk+1(xk+1)} fn+1(xn+1)=1 k=n,n-1,…,2,1
例6某工厂设计一种电子设备,由D1,D2,D3串联组 成。已知三种元件的单价和可靠性如下表所示, 要求设计 中所使用的费用不超过105元。试问应如何设计, 可使设 备的可靠性最大? 元件 单价ck(元) 可靠性pk D 30 0.9 D2 15 0.8 D; 20 0.5 解:按元件种类分成三个阶段,k=1,2,3;设状态 变量x表示从元件D到D3允许使用的费用;决策变量u为 部件D所使用的并联元件个数;则Xk+1=XC山k 用可靠 性作为指标,则部件的可靠性为1-(1-pk)。 记(xk)为部件D至部件D3的最大工作可靠性,则 「东(xk)=max{[1-(1-pk)u]f+1(X+1) f(x4)=1 k=3,2,1
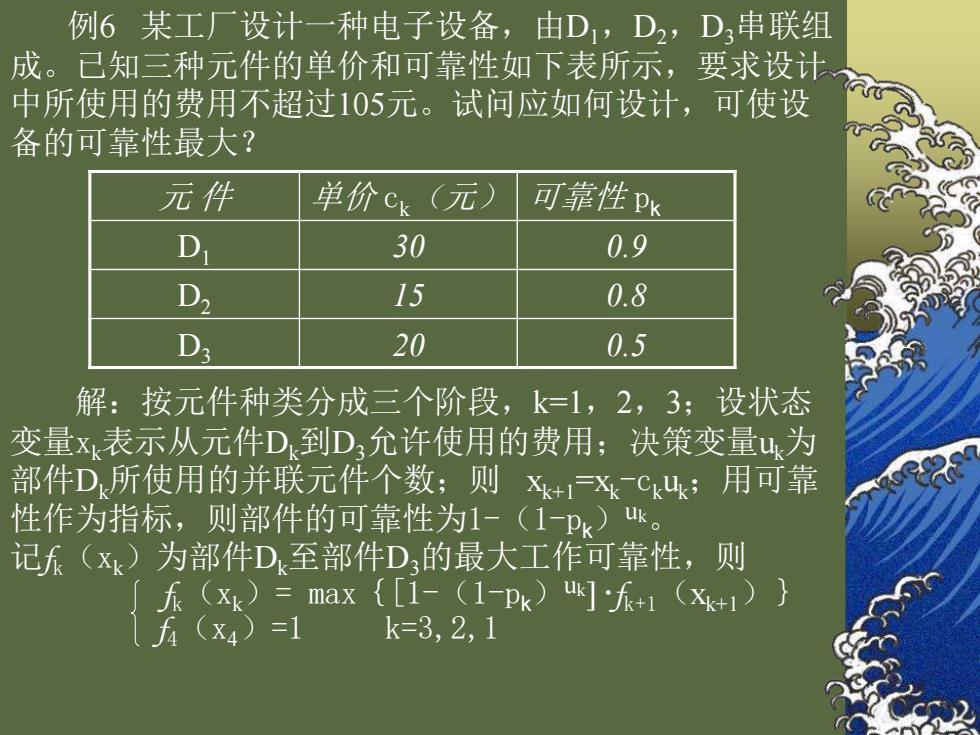
例6 某工厂设计一种电子设备,由D1,D2,D3串联组 成。已知三种元件的单价和可靠性如下表所示,要求设计 中所使用的费用不超过105元。试问应如何设计,可使设 备的可靠性最大? 元 件 单价 ck(元) 可靠性 pk D1 30 0.9 D2 15 0.8 D3 20 0.5 解:按元件种类分成三个阶段,k=1,2,3;设状态 变量xk表示从元件Dk到D3允许使用的费用;决策变量uk为 部件Dk所使用的并联元件个数;则 xk+1=xk-ckuk;用可靠 性作为指标,则部件的可靠性为1-(1-pk)uk 。 记fk(xk)为部件Dk至部件D3的最大工作可靠性,则 fk(xk)= max{[1-(1-pk)uk] ·fk+1(xk+1)} f4(x4)=1 k=3,2,1

k=3x3={105-(30+15)}, {105-(30+15×2)} {105-(30+15×3))或(105-(30×2+15) =60,45,30 5(30)=0.5 u3(30)=1 5(45)=1-(1-0.5)2=0.75 山3(45)=2 5(60)=1-(1-0.5)3=-0.875 山(60)=3 k=2x2={105-30},{105-(30×2)}=75,45 5(45)=0.85(30)=0.8×0.5=0.4 2(45)=12 [1-(1-0.8)3]5(30) 0.992×0.5 五(75)=max1-(1-0.8)2]5(45) =max 0.96×0.75 0.85(60) 0.8×0.875 =max{0.496,0.72,0.7}=0.72 2(75)=2 k=1X1=105 f(105)=max{[1-(1-0.9)2]5(45),0.95(75)} =max{0.99×0.4,0.9×0.72} =max{0.396,0.648}=0.648 u1(105)=1 最优设计方案:D=1(个);D2=2(个);D,=2(个狼 最大可靠性为0.648,总费用100元
k=3 x3 ={105-(30+15)},{105-(30+15×2)}, {105-(30+15×3)}或{105-(30×2+15)} =60,45,30 f3(30)=0.5 u3(30)=1 f3(45)=1-(1-0.5)2=0.75 u3(45)=2 f3(60)=1-(1-0.5)3=0.875 u3(60)=3 k=2 x2 ={105-30},{105-(30×2)}=75,45 f2(45)=0.8·f3(30)=0.8×0.5=0.4 u2(45)=1 [1-(1-0.8)3]·f3(30) 0.992×0.5 f2(75)=max [1-(1-0.8)2]·f3(45)=max 0.96×0.75 0.8·f3(60) 0.8×0.875 =max{0.496,0.72,0.7}=0.72 u2(75)=2 k=1 x1=105 f1(105)=max{[1-(1-0.9)2]·f2(45),0.9·f2(75)} =max{0.99×0.4,0.9×0.72} =max{0.396,0.648}=0.648 u1(105)=1 最优设计方案:D1=1(个);D2=2(个);D3=2(个) 最大可靠性为0.648,总费用100元