
第一章线性规划与单纯形法 本章内容简要回顾 在这一章里,我们首先由两个实际问题引出了线性规划的数学模型。 线性规划问题实际就是在一组线性不等式或等式约束条件下,求某一线 性目标函数的最大或最小值的优化问题。我们通过具有两个决策变量的 线性规划问题的图解法,对线性规划问题的解、可行解、可行域及最优 解有了一个初步直观的认识,那就是:具有两个决策变量的线性规划问 题的可行域是凸多边形:若线性规划问题存在最优解,则一定能在可行 域的某个顶点得到。 接着,我们规定了线性规划的标准型,给出了线性规划的基、基解 以及基可行解的概念;还给出了凸集及其顶点的定义。在此基础上,通 过三个定理的论证,对图解法的结论加以拓展,得出了如下结论: 1、线性规划问题的可行域是凸集: 2、该凸集的每个顶点都对应一个基可行解,因基可行解个数是有限 的,从而凸集的顶点也是有限的: 3、若线性规划问题存在最优解,则一定能在可行域的某个顶点达到, 亦即在有限个基可行解中找到。上述结论就是求解线性规划的通用方 单纯形法的理论基础
第一章 线性规划与单纯形法 一、本章内容简要回顾 在这一章里,我们首先由两个实际问题引出了线性规划的数学模型。 线性规划问题实际就是在一组线性不等式或等式约束条件下,求某一线 性目标函数的最大或最小值的优化问题。我们通过具有两个决策变量的 线性规划问题的图解法,对线性规划问题的解、可行解、可行域及最优 解有了一个初步直观的认识,那就是:具有两个决策变量的线性规划问 题的可行域是凸多边形;若线性规划问题存在最优解,则一定能在可行 域的某个顶点得到。 接着,我们规定了线性规划的标准型,给出了线性规划的基、基解 以及基可行解的概念;还给出了凸集及其顶点的定义。在此基础上,通 过三个定理的论证,对图解法的结论加以拓展,得出了如下结论: 1、线性规划问题的可行域是凸集; 2、该凸集的每个顶点都对应一个基可行解,因基可行解个数是有限 的,从而凸集的顶点也是有限的; 3、若线性规划问题存在最优解,则一定能在可行域的某个顶点达到, 亦即在有限个基可行解中找到。上述结论就是求解线性规划的通用方 法——单纯形法的理论基础

随后,我们详细讲述了单纯形表的结构、最优解判定定 理、无界解判定定理和单纯形法的解题步骤。 步骤1化为标准形(要求b≥0),确定初始基B(=E) 建立初始单纯形表。 步骤2检查非基变量的检验数,若所有o;=C-CBP≤0, 则已得最优解,计算停;否则按max{o:>0}=ok,确定X为 旋入变量。 步骤3若对于σ>0,有B1P0(即单纯形表中X对应的 系数列向量非正),则该问题无有限最优解,计算停;否则 转步骤4。 步骤4计算0=mm((B-b),/ak|ak>0}=(B-b)/a,k确 定单纯形表中第L行对应的基变量为旋出变量 步骤5以ak为主元作(L,K)旋转变换,得新的单纯形 表,转步骤2 本章最后,我们还介绍了求解线性规划的两阶段法以及 根据实际问题建立线性规划数学模型的几个例题
随后,我们详细讲述了单纯形表的结构、最优解判定定 理、无界解判定定理和单纯形法的解题步骤。 步骤1 化为标准形(要求b≥0),确定初始基B(=E), 建立初始单纯形表。 步骤2 检查非基变量的检验数,若所有 ≤0, 则已得最优解,计算停;否则按 {σj >0}=σk,确定Xk为 旋入变量。 步骤3 若对于σk>0,有B-1Pk≤0(即单纯形表中Xk对应的 系数列向量非正),则该问题无有限最优解,计算停;否则 转步骤4。 步骤4 计算 θ= {(B -1b)i/aik│aik>0}=(B -1b)ι/aιk,确 定单纯形表中第L行对应的基变量为旋出变量。 步骤5 以aιk为主元作(L,K)旋转变换,得新的单纯形 表,转步骤2。 本章最后,我们还介绍了求解线性规划的两阶段法以及 根据实际问题建立线性规划数学模型的几个例题。 j 1 σj Cj - CBB P − = max j i mim

应重点掌握的问题 1、根据实际问题建立线性规划数学模型: 2、用单纯形法求解线性规划。 三、 典型例题分析 1、建模 某厂生产A、B、C三种产品,消耗三种资源,已知单位产品消耗资 源数量及单位产品销售利润如下表所列: 资源 煤 工时 电 利润 产品 (吨) (小时) (度) (元) A 8 20 5 85 B 6 18 96 C 10 1 6 100 个月 内生产上可利用的煤为P吨,可利用的工时为Q小时,工厂在 个月内完成的利润不少于R元,在恰好用完工时的条件下,如何安排生 立, 可使耗电量最省? 解:设产品A、B、C各生产x1,x2,x个单位,则线性规划数学模型为 minZ=5x +8x2+6x
二、应重点掌握的问题 1、根据实际问题建立线性规划数学模型; 2、用单纯形法求解线性规划。 三、典型例题分析 1、建模 某厂生产A、B、C三种产品,消耗三种资源,已知单位产品消耗资 源数量及单位产品销售利润如下表所列: 一个月内生产上可利用的煤为P吨,可利用的工时为Q小时,工厂在 一个月内完成的利润不少于R元,在恰好用完工时的条件下,如何安排生 产,可使耗电量最省? 解:设产品A、B、C各生产x1 ,x2 ,x3个单位,则线性规划数学模型为 minZ=5x1+8x2+6x3 资源 产品 煤 (吨) 工时 (小时) 电 (度) 利润 (元) A B C 8 6 10 20 18 15 5 8 6 85 96 100

8x1+6x2+10x≤P 20x+18x+15x4=Q 85x+96x+100x4≥R X1,X2,X320 2、求解下列线性规划 maxZ=3x-X2-X3 X1-2x2+X3≤11 -4x1+ X2+2X3≥3 -2x1 1,X2,X3≥0 解 方法 大M法,详见教材P16~P17。 方法二: 两阶段法,详见教材P18P19
8x1+6x2+10x3 ≤P 20x1+18x3+15x4=Q 85x1+96x3+100x4 ≥R x1 ,x2 ,x3 ≥0 2、求解下列线性规划 maxZ=3x1 -x2 -x3 x1 -2x2 + x3≤11 -4x1 + x2 +2X3≥3 -2x1 + x3 =1 x1 ,x2 ,x3 ≥0 解 方法一:大M法,详见教材P16~P17。 方法二:两阶段法,详见教材P18~P19

第二章线性规划的对偶理论与灵敏度分析 一、本章内容简要回顾 在这一章里,我们首先由第一章的实际问题引出了线性规划的对偶 问题,阐明了线性规划原问题与其对偶问题的关系;。 接着,论证了对偶问题的五个重要性质:在此基础上, 讲述了求解线 性规划的对偶单纯形法,其计算步骤如下: 步骤1确定原问题的初始基B,使所有检验数O;=C;-CBP;≤0 即Y=CB'是对偶可行解,建立初始单纯形表 步骤2检查基变量的取值,若XBb≥0,则已得最优解,计算停: 否则求 min{(Bb),|(Bb),<0}=(Bb) 确定单纯形表第L行对应的基变量为旋出变量。 步骤3若所有a,≥0,则原问题无可行解,计算停; 否则,计算 0=min (oilaul a<0)=ok/ak 确定对应的x为旋入变量。 步骤4以k为主元作(L,K)旋转变换,得新的单纯形表,转步骤2。 本章还介绍了对偶问题的经济意义一影子价格。 对偶最优解Y=CB=(y1,y2,,y),y表示在原问题已取得最优解的情 况下,第种资源增加一个单位时总收益的增加值,也可以说y是对第 种资源的一种价格估计。这种价格估计并不是第种资源的实际价值或 成本,而是由该企业在制产品的收益来估计所用资源的单位价值,它 是一种潜在的价格称为影子价格。 nULU
第二章 线性规划的对偶理论与灵敏度分析 一、本章内容简要回顾 在这一章里,我们首先由第一章的实际问题引出了线性规划的对偶 问题,阐明了线性规划原问题与其对偶问题的关系;。 接着,论证了对偶问题的五个重要性质;在此基础上,讲述了求解线 性规划的对偶单纯形法,其计算步骤如下: 步骤1 确定原问题的初始基B,使所有检验数 , 即Y=CBB-1是对偶可行解,建立初始单纯形表。 步骤2 检查基变量的取值,若XB=B-1b≥0,则已得最优解,计算停; 否则求 min{(B-1b)i│(B-1b)i<0}=(B-1b)ι 确定单纯形表第L行对应的基变量为旋出变量。 步骤3 若所有aιj≥0,则原问题无可行解,计算停;否则,计算 θ=min{σj / aιj│ aιj <0 }=σk /aιk 确定对应的xk为旋入变量。 步骤4 以aιk为主元作(L,K)旋转变换,得新的单纯形表,转步骤2。 本章还介绍了对偶问题的经济意义——影子价格。 对偶最优解Y= CBB -1=(y1,y2,…,ym ), yi表示在原问题已取得最优解的情 况下,第i种资源增加一个单位时总收益的增加值,也可以说yi是对第i 种资源的一种价格估计。这种价格估计并不是第i种资源的实际价值或 成本,而是由该企业在制产品的收益来估计所用资源的单位价值,它 是一种潜在的价格,称为影子价格。 C - C B Pj 0 1 σj j B − =

企业可以将资源的影子价格与市场价格比较,来决定是购 入还是出让该种资源。当某资源的市场价格低于影子价格时, 企业应该买进该资源用于扩大生产;而当市场价格高于影子 价格时,则企业的决策者应该将已有资源买掉。这样获利会 更多。 利用单纯形表求解线性规划,在求得最优解的同时,很 容易得到问题的各种资源的影子价格。某资源的影子价格, 就是该资源对应的约束条件所加松弛变量在最优表中的检验 数的相反数。 本章最后详细讲述了线性规划某些系数或限制述变动的 灵敏度分析,以及参数线性规划问题。 二、应重点掌握的问题 1、用对偶单纯形法求解线性规划问题; 2、对偶问题的经济意义 影子价格; 3、灵敏度分析
企业可以将资源的影子价格与市场价格比较,来决定是购 入还是出让该种资源。当某资源的市场价格低于影子价格时, 企业应该买进该资源用于扩大生产;而当市场价格高于影子 价格时,则企业的决策者应该将已有资源买掉。这样获利会 更多。 利用单纯形表求解线性规划,在求得最优解的同时,很 容易得到问题的各种资源的影子价格。某资源的影子价格, 就是该资源对应的约束条件所加松弛变量在最优表中的检验 数的相反数。 本章最后详细讲述了线性规划某些系数或限制述变动的 灵敏度分析,以及参数线性规划问题。 二、应重点掌握的问题 1、用对偶单纯形法求解线性规划问题; 2、对偶问题的经济意义——影子价格; 3、灵敏度分析
、 典型例题分析 1、用对偶单纯形法求解下述问题 minZ=12x1+8x2+16x3+12x4 2x1+2+4X3≥2 2x1+2x2+4x1≥3 X1,X2,X3,X4≥0 求解过程详见教材P36~37 2、灵敏度分析 某工厂生产A、B两种产品,每生产一吨产品所需的原 料 工时和提供的利润以及资源的限制量如下表: 资源 产品 A B 总 量 原 料(吨) 2 3 100 工 时(小时) 4 2 120 利润(百元/吨) 6 4 (1)试确定获利最大的生产方案; 当原料的市场价格为 0.2百元/吨时,企业是否应该多购进原料以扩大生产规模?
三、典型例题分析 1、用对偶单纯形法求解下述问题 minZ=12x1+8x2+16x3 +12x4 2x1+ x2 +4x3 ≥2 2x1+2x2+4x4 ≥3 x1 ,x2 ,x3 ,x4≥0 求解过程详见教材P36~37。 2、灵敏度分析 某工厂生产A、B两种产品,每生产一吨产品所需的原 料、工时和提供的利润以及资源的限制量如下表: 资源 产品 A B 总 量 原 料 (吨) 工 时(小时) 2 3 4 2 100 120 利 润( 百元/吨) 6 4 (1)试确定获利最大的生产方案;当原料的市场价格为 0.2百元/吨时,企业是否应该多购进原料以扩大生产规模?

2)当产品A的利润由6百元/吨增至12百元/吨时,是否需要 修改原计划?若需要修改,求新的最优生产方案, (3)若工时总量增至240小时,求最优方案, (4)若新研制出一种产品C,每生产一吨该产品需原料4吨! 工时3小时,可获利8百元,试问该厂是否应该生产新产品C?如果 生产,应该生产多少? (5)若生产中,又增加了用电量的限制,已知每生产1吨产品 A、B用电量分别为2,3个单位,计划期内电量限制在90个单 位之内,试分析原最优解有无变化?如果有变化,求出新的 最优解。 解: (1)设生产A、B两种产品的产量分别为x,X,则该 问题的线性规划数学模型为: maxZ=6x +4x 2x1+3x≤100 4x1+2x≤120 X1,X2≥0
(2)当产品A的利润由6百元/吨增至12百元/吨时,是否需要 修改原计划?若需要修改,求新的最优生产方案; (3)若工时总量增至240小时,求最优方案; (4)若新研制出一种产品C,每生产一吨该产品需原料4吨, 工时3小时,可获利8百元,试问该厂是否应该生产新产品C?如果 生产,应该生产多少? (5)若生产中,又增加了用电量的限制,已知每生产1吨产品 A、B用电量分别为2,3个单位,计划期内电量限制在90个单 位之内,试分析原最优解有无变化?如果有变化,求出新的 最优解。 解:(1)设生产A、B两种产品的产量分别为x1 ,x2,则该 问题的线性规划数学模型为: maxZ=6x1+4x2 2x1+3x2 ≤100 4x1+2x2 ≤120 x1 ,x2 ≥0
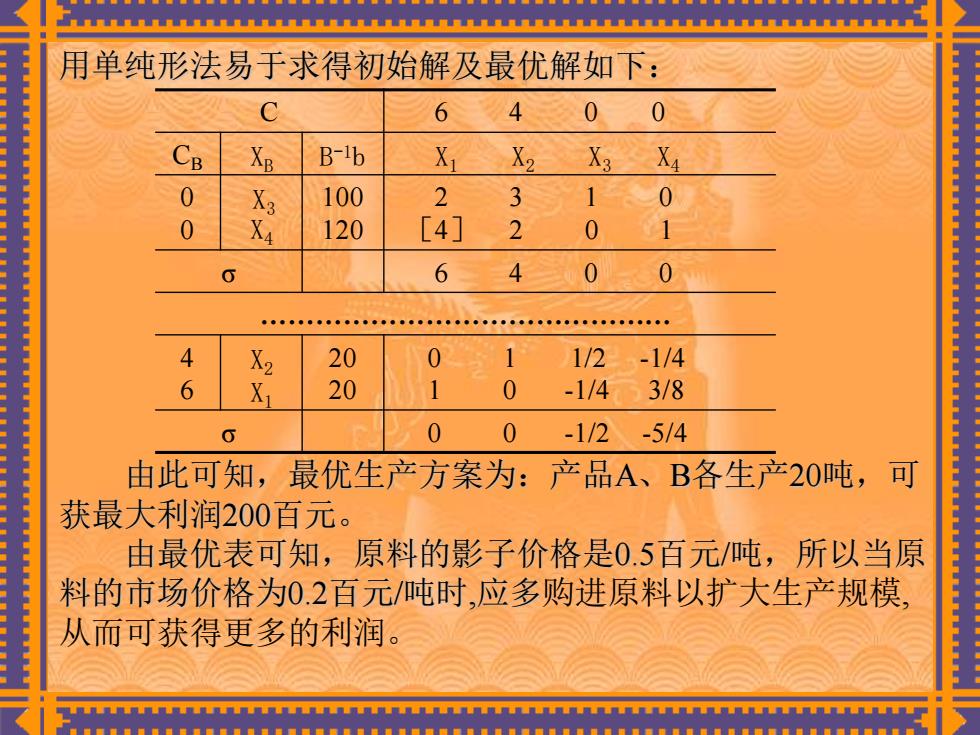
用单纯形法易于求得初始解及最优解如下: 6 B XB B-1b X 100 2 120 [4] 2 0 0 20 1/2 -1/4 X 20 -1/4 3/8 0 -1/2 -5/4 由此可知,最优生产方案为:产品A、B各生产20吨,可 获最大利润200百元。 由最优表可知,原料的影子价格是0.5百元/吨,所以当原 料的市场价格为02百元/吨时,应多购进原料以扩大生产规模 从而可获得更多的利润
C 6 4 0 0 CB XB B -1b X1 X2 X3 X4 0 0 X3 X4 100 120 2 3 1 0 [4] 2 0 1 σ 6 4 0 0 ……………………………………… 4 6 X2 X1 20 20 0 1 1/2 -1/4 1 0 -1/4 3/8 σ 0 0 -1/2 -5/4 用单纯形法易于求得初始解及最优解如下: 由此可知,最优生产方案为:产品A、B各生产20吨,可 获最大利润200百元。 由最优表可知,原料的影子价格是0.5百元/吨,所以当原 料的市场价格为0.2百元/吨时,应多购进原料以扩大生产规模, 从而可获得更多的利润

(2)将C,=12代入原最优表,重新计算检验数,原最优解不 再是最优解,所以需要修改原计划。以原最优解为初始解, 用单纯形法继续运算,结果如下: C 12 4 0 0 CB X B-ib X1 X2 X3 X4 4 X2 20 0 1 1/2 -114 12 20 1 0 -1/4 3/8 O 0 0 -7/2 0 X3 40 0 2 1-1/2 12 30 1/2 0 1/4 -2 0 -3 新的最优方案是:X=30,X=40,X2=X40 最优值:Z=360
(2)将C1=12代入原最优表,重新计算检验数,原最优解不 再是最优解,所以需要修改原计划。以原最优解为初始解, 用单纯形法继续运算,结果如下: C 6 4 0 0 CB XB B -1b X1 X2 X3 X4 4 6 X2 X1 20 20 0 1 1/2 -1/4 1 0 -1/4 3/8 σ 0 0 -1/2 -5/4 12 12 1 -7/2 0 12 X3 X1 40 30 0 2 1 -1/2 1 1/2 0 1/4 σ 0 -2 0 -3 新的最优方案是:X1=30,X3=40,X2 =X4=0 最优值:Z=360