
§4单服务台排队系统模型(MWMM) 本节将讨论输入为普阿松流,服务时间为负指数分布的单服务 台排队系统模型。因为这类模型都符合生灭过程,所以可以将生灭 过程的结论搬过来应用。 ◆ 下面分几种类型来讨论。 4.1M/M/1/oo/oo模型 ◆ 该模型是指顾客按普阿松流到达,到达速率为入,服务时间服 从负指数分布,服务速率为山,单个服务台,系统对顾客无限制, 顾客源也无限制,先到先服务的服务系统。其系统状态是无限的, 即=0,1,2,..。图10—4表示系统的状态转移图。 图10一4
§4 单服务台排队系统模型(M/M/1) 本节将讨论输入为普阿松流,服务时间为负指数分布的单服务 台排队系统模型。因为这类模型都符合生灭过程,所以可以将生灭 过程的结论搬过来应用。 下面分几种类型来讨论。 4.1 M/M/1/∞/∞模型 该模型是指顾客按普阿松流到达,到达速率为λ ,服务时间服 从负指数分布,服务速率为μ ,单个服务台,系统对顾客无限制, 顾客源也无限制,先到先服务的服务系统。其系统状态是无限的, 即n=0,1,2,…。图10—4表示系统的状态转移图。 0 1 2 n-1 n n+1 λ λ λ λ λ λ λ μ μ μ μ μ μ μ ● ● ● ● ● ● ● ● ● ● ● 图10—4

因为对所有状态n,n=入,4n,所以 C=(Nu)=pm (n=1,2,..》 Pn=CnPo-p"Po, 1 P0= 00 C. 1=1-P ∑p 拉三0 Pn=(1-p)p" 这里p=μ<1是单位时间顾客平均到达率与平均服务率的比值,反映 了服务机构的忙碌或利用程度,称为服务强度或服务的忙期。因为 p≥时,系统内顾客数会越来越多,系统无法进入稳定状态,所以 设p<1。 下面推导服务系统的其它指标: Ls=nP=(1-pn匹(1-p)p pp -ppp n=0 三 1p2pu-元 L2n-P2R-l。(1-)L,p=l.M =1 4-元
Cn =(λ/μ)n=ρ n (n=1,2, …) Pn = CnP0=ρ nP0, P0= =1-ρ 因为对所有状态n ,λn =λ,μn =μ,所以 = = = n 0 n n 0 ρ 1 C 1 n Pn =(1-ρ)ρ n 这里ρ=λ/μ<1是单位时间顾客平均到达率与平均服务率的比值,反映 了服务机构的忙碌或利用程度,称ρ为服务强度或服务的忙期。因为 ρ≥1时,系统内顾客数会越来越多,系统无法进入稳定状态,所以 设ρ<1。 下面推导服务系统的其它指标: Ls= =(1-ρ) =(1-ρ)ρ = = Lq= =Ls-(1-P0)=Ls-ρ=Ls-λ/μ = n=0 nPn n=0 nρn μ λ λ − = − = − = − − • • 1 ρ ρ ρ 1 ρ ρ 1 ρ 1 ρ ρ 1 2 1- 1 dρ d − = • n 0 ρ n dρ 1 ρ ρ d n =0 ρ n dρ d = − = = = n 1 n n 1 n n 1 n-1Pn nP P − − = − μμ λ λ μ λ μλ λ 2

Wj-L:MA- u-元 W。LgA= u-入 下面再计算:顾客在系统中停留时间超过的概率是多少?假定 顾客来到系统时,系统中已有个人,则该顾客在系统中的停留时 间应该是系统对前个顾客的服务时间加上对他的服务时间。若分 别用T,T2,,Tn表示前个顾客的服务时间,Tm+1表示对该顾客 的服务时间,令Sn+1=T+T2+..+Tn+Tn+1,则Sn+/满足n+1阶爱尔朗 分布,参数为u。 可以证得其密度函数为∫(S+)=片e-: p (S)=(ted 顾客在系统中停留时间小于的概率 P (W<i)=2 ,P(S)=高p)p j暘ed u(1-p)e4 dt=∫du-jee-t1dt=l-e-a n=0 n!
Ws =Ls /λ= Wq =Lq /λ= μλ 1 − μμ −λ λ 下面再计算:顾客在系统中停留时间超过t的概率是多少?假定一个 顾客来到系统时,系统中已有n个人,则该顾客在系统中的停留时 间应该是系统对前n个顾客的服务时间加上对他的服务时间。若分 别用T1,T2,…,Tn表示前n个顾客的服务时间, Tn+1 表示对该顾客 的服务时间,令Sn+1 =T1+ T2 +…+Tn+Tn+1 ,则Sn+1满足n+1阶爱尔朗 分布,参数为μ。 可以证得其密度函数为 f(Sn+1)= P{Sn+1 ≤t}= 顾客在系统中停留时间小于t的概率 P{W≤t}= PnP{Sn+1≤t}= (1-ρ)ρ n ( ) n μt μt e n! μ − ( ) t − 0 n μt μt t n! μ e d n=0 n=0 ( ) t − 0 n μt μt t n! μ e d ( ) (μ-λ)t t 0 t μ t λ t 0 n μ t μ1- e t μ- e e t e n! μ t − − − = − = = = − ρ λ 1 n 0 ρ d d

即W服从参数为uA的负指数分布。 所以顾客在系统中停留时间大于的概率 P {W>t)=1-P (W<t}=e-(A) 例1某超级市场,顾客按普阿松流来到唯一的收款合。已知平 均每小时来到20人,记价收款时间服从负指数分布,平均每个顾客 需2.5分钟,试求该超级市场收款台的有关运行指标。 解:根据题意,这是MWMW1/oo/oo模型, =20/60=1/3,u=1/2.5,p=W=5/6 系统有关指标计算如下: (1)P。=1-p=1-5/6=1/6,忙期概率为1-Po=p=5/6 2)系统内顾客平均值L。= ·=1/3÷(1/2.5-1/3)=5(人) 3排队等待顾客平均值L,:M455/6-4.167(人) (4)每个顾客在系统内平均逗留时间 W。=Ls八=5÷(1/3)=15(分钟) (⑤)每个顾客在队列中平均逗留时间W。W。-1u=12.5(分钟)
即W服从参数为μ-λ的负指数分布。 所以顾客在系统中停留时间大于t的概率 P{W>t}=1-P{W≤t}=e -(μ-λ)t 例1 某超级市场,顾客按普阿松流来到唯一的收款台。已知平 均每小时来到20人,记价收款时间服从负指数分布,平均每个顾客 需2.5分钟,试求该超级市场收款台的有关运行指标。 解:根据题意,这是M/M/1/∞/∞模型, λ=20/60=1/3,μ=1/2.5,ρ=λ/μ=5/6 系统有关指标计算如下: ⑴ P0=1-ρ=1-5/6=1/6,忙期概率为 1-P0=ρ=5/6 ⑵系统内顾客平均值 Ls= =1/3÷(1/2.5-1/3)=5(人) ⑶排队等待顾客平均值Lq =Ls-λ/μ=5-5/6=4.167 (人) ⑷每个顾客在系统内平均逗留时间 Ws =Ls /λ=5÷(1/3)=15(分钟) ⑸每个顾客在队列中平均逗留时间Wq = Ws-1/μ=12.5(分钟) μ λ λ −
4.2MWMI1/NWoo模型 在实际生活中经常会碰到队长有限制的服务系统,如医院规定 每天挂100个号,那么第100个以后到达者会自动离开服务系统:理 发店内等待的座位都满员时,后来的顾客就会离开,等等。因为队 长有限制,所以系统的状态只能取0,1,2,,这些值。系统状 态转移图如图10一5所示。 图10-5 , 入m{0, 当n=0,1,2,N-1 当≥N 4n=u, n=1,2,.…,N _(/)n=p,对n=0,1,2,…,N C0, 对n>N 于是,P=N =1-p pm Pn=C,Po-p"Po0.1.2...N n=0
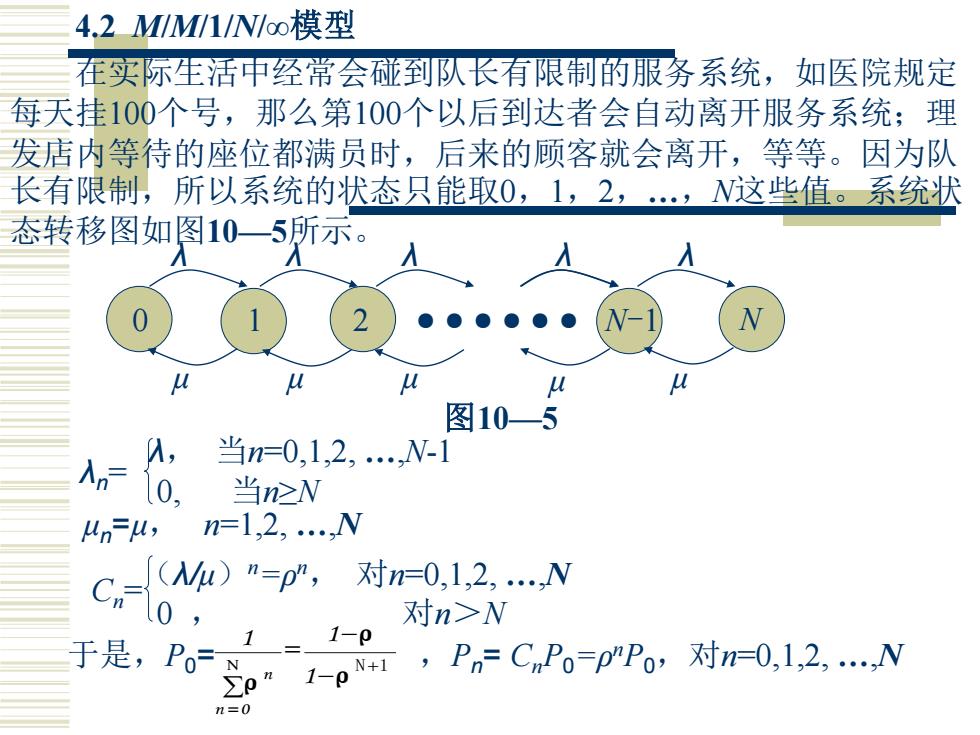
4.2 M/M/1/N/∞模型 在实际生活中经常会碰到队长有限制的服务系统,如医院规定 每天挂100个号,那么第100个以后到达者会自动离开服务系统;理 发店内等待的座位都满员时,后来的顾客就会离开,等等。因为队 长有限制,所以系统的状态只能取0,1,2,…,N这些值。系统状 态转移图如图10—5所示。 0 1 2 N-1 N μ μ μ μ μ ● ● ● ● ● ● 图10—5 λ λ λ λ λ λ, 当n=0,1,2, …,N-1 0, 当n≥N λn = μn =μ, n=1,2, …,N (λ/μ)n=ρn , 对n=0,1,2, …,N 0 , 对n>N Cn = 于是,P0= ,Pn = CnP0=ρn N+1 P0,对n=0,1,2, …,N = − − = ρ ρ ρ 1 1 1 n 0 n N

由此 L= nPa= n- 1-p 1-0N+20 dpn 1-p d ∑p” 1-p 1-oN1 ed 1-o 1-p N+1dp 1-0 (N+1)pN+1 1-0 N+1 与MWMW1/oo/oo模型中的Ls比较,两个表达式第一项相同,差别 是多 了一项:(N+1pN+ 1-0N+i 由于p<1,容易看出:在队长受限制情况下,系统中顾客数一定小 于队长不受限制时系统中的顾客数;另外当N→o时,L。一 与队长不受限制时系统中的顾客平均数完全一致。因此,队长不受 限制系统可看作队长受限制系统的一种特例。 为了计算系统其它各项指标,先要引进有效输入率的概念。 因为在队长受限制的情况下,当到达的顾客数心时,新来的顾客
由此 Ls= = = N n 0 nPn ( ) − − = − = − + + + + = = ρ -ρ ρ -ρ ρ ρ ρ -ρ ρ ρ ρ -ρ ρ n 0 n n 0 n 1 1 N 1 N 1 N 1 N 1 N 1 N 1 1 1 1 1 dρ d dρ d dρ d N 1 N 1 1 N 1 1 + + − + − − = ρ ρ ρ ρ 与M/M/1/∞/∞模型中的Ls比较,两个表达式第一项相同,差别 是多了一项: N 1 N 1 1 N 1 + + − + ρ ρ 由于ρ<1 ,容易看出:在队长受限制情况下,系统中顾客数一定小 于队长不受限制时系统中的顾客数;另外当N→∞时,Ls→ , 与队长不受限制时系统中的顾客平均数完全一致。因此,队长不受 限制系统可看作队长受限制系统的一种特例。 为了计算系统其它各项指标,先要引进有效输入率λeff 的概念。 因为在队长受限制的情况下,当到达的顾客数n≥N时,新来的顾客 ρ ρ 1−

会自动离去。因此虽然顾客以平均为入的速率来到服务系统,但由 于WO,真正进入服务系统的顾客平均输入率却是小于的入f· Aer=XnPn=1P斤A(1-PN 0 n=0 可以验证 ef=u(1-Po) 由此可以算得:Lg=Ls(1-Po)=Ls入er/u Wg=Ls八ef Wg=Lg/Aent=Ws-1lu 例2某个单人理发店,备有六张椅子供顾客等待理发。当椅子 坐满时,后来的顾客不再进入而自动离去。已知平均每小时到达3 名顾客,每名顾客理发时间平均是15分钟。试求 (1)顾客无需等待就可理发的概率; (2)店内顾客平均数; (3)有效到达率; (④)需要等待的顾客平均数; (5)顾客在店内平均逗留时间; (6)顾客等待理发的平均时间;
会自动离去。因此虽然顾客以平均为λ的速率来到服务系统,但由 于λN=0,真正进入服务系统的顾客平均输入率却是小于λ的λeff 。 λeff = =λ(1-PN) 可以验证 λeff =μ(1-P0) = − = = N N 1 λ λ n 0 n n 0 nPn P 由此可以算得: Lq =Ls-(1-P0)=Ls-λeff /μ Ws =Ls /λeff Wq =Lq /λeff =Ws-1/μ 例2 某个单人理发店,备有六张椅子供顾客等待理发。当椅子 坐满时,后来的顾客不再进入而自动离去。已知平均每小时到达3 名顾客,每名顾客理发时间平均是15分钟。试求 ⑴顾客无需等待就可理发的概率; ⑵店内顾客平均数; ⑶有效到达率; ⑷需要等待的顾客平均数; ⑸顾客在店内平均逗留时间; ⑹顾客等待理发的平均时间;

(⑦)有百分之几的顾客因客满而自动离去。 解:这个问题可以归结为MM1/7/oo模型, =3(人/小时),=4(人/小时),据此可以求出: (1)顾客无需等待就可理发的概率:Po 1-p 1-3/4 1-pN+1 1-3/4)8 ≈0.2778 (2)店内顾客平均数: N+10N+1 i品。 3/4 8×3/4)8 ≈2.11(人) (3)有效到达率: 1-pN+1 1-3/4 1-3/4)8 入er4(1-P)=4×(1-0.2778)≈2.89 (人/小时) (4)需要等待的顾客平均数: Lg=Ls(1-Po)≈2.11-1+0.28=1.39(人) (5)顾客在店内平均逗留时间: Wg=Ls小er=2.11÷2.89≈0.73(小时)=43.8(分) (6)顾客等待理发的平均时间: W。=W、-1/u=43.8-15=28.8(分) (7)P7=p7Po=(3/4)7X0.2778≈0.037=3.7%
⑺有百分之几的顾客因客满而自动离去。 解:这个问题可以归结为M/M/1/7/∞模型, λ=3(人/小时),μ=4(人/小时),据此可以求出: ⑴顾客无需等待就可理发的概率:P0= ≈0.2778 ⑵店内顾客平均数: Ls ≈2.11(人) ⑶有效到达率: λeff =μ(1-P0)=4×(1-0.2778)≈2.89(人/小时) ⑷需要等待的顾客平均数: Lq =Ls-(1-P0)≈2.11-1+0.28=1.39(人) ⑸顾客在店内平均逗留时间: Ws =Ls /λeff =2.11÷2.89≈0.73(小时)=43.8(分) ⑹顾客等待理发的平均时间: Wq=Ws-1/μ =43.8-15=28.8(分) ⑺ P7=ρ7P0=(3/4)7×0.2778≈0.037=3.7% 8 1 3/4 1 3/4 − − = − − ρN+1 ρ 1 1 8 8 N 1 N 1 1 3/4 8 3/4 1 3/4 3/4 1 N 1 1 − − − = − + − − = + + ρ ρ ρ ρ

4.3M/M/1/oo/m模型(顾客源有限) 现在来分析顾客源有限的排队问题。这类排队问题的主要特征 是顾客总数是有限的,如只有m个顾客。每个顾客来到系统中接受 服务后仍回到原来的总体,还有可能再来。这类问题在工业生产中 遇到的较多,最典型的例子是机器看管问题。如一个工人同时看管 台机器,当机器发生故障时即停下来等待修理,修好后再投入使 用,且仍然可能再发生故障。类似的例子还有m个打字员共用一台 打字机,m个终端共用一台打印机等等。 关于顾客的平均到达率,在无限源的情形中是按全体顾客来考 虑的,而在有限源的情形下,必须按每一顾客来考虑。假定每个顾 客来到服务系统的时间间隔均服从参数为入的负指数分布,则表示 单个顾客的平均到达率(其含义是指单位时间内该顾客来到系统请 求服务的次数)。当顾客总数为m,而系统内有个顾客时,顾客 总的平均到达率为(-n)入,因此顾客源有限的排队模型也可以用生灭 过程的状态转移图来表示如下:
4.3 M/M/1/∞/m 模型(顾客源有限) 现在来分析顾客源有限的排队问题。这类排队问题的主要特征 是顾客总数是有限的,如只有m个顾客。每个顾客来到系统中接受 服务后仍回到原来的总体,还有可能再来。这类问题在工业生产中 遇到的较多,最典型的例子是机器看管问题。如一个工人同时看管 m台机器,当机器发生故障时即停下来等待修理,修好后再投入使 用,且仍然可能再发生故障。类似的例子还有m个打字员共用一台 打字机,m个终端共用一台打印机等等。 关于顾客的平均到达率,在无限源的情形中是按全体顾客来考 虑的,而在有限源的情形下,必须按每一顾客来考虑。假定每个顾 客来到服务系统的时间间隔均服从参数为λ的负指数分布,则λ表示 单个顾客的平均到达率(其含义是指单位时间内该顾客来到系统请 求服务的次数)。当顾客总数为m ,而系统内有n个顾客时,顾客 总的平均到达率为(m-n)λ,因此顾客源有限的排队模型也可以用生灭 过程的状态转移图来表示如下:

图10—6 m (m-0入 (m-2)M 2 ∫(m-n)M,当n=0,1,2,,m m10, 当n>m 4n=u,=1,2,,m -2-2…_(m-n+1(m-n+22…m-1八m2 C=T nun- mm-少-m-n哈n厂当n=2m Cn=0,当n>m P-CPo-n n=1,2,,m
0 1 2 m-1 m μ μ μ μ μ ● ● ● ● ● ● mλ (m-1)λ 2λ λ 图10—6 (m-n)λ,当n=0,1,2, …, m 0, 当n>m μn =μ, n=1,2, …, m λn = Cn = ( ) , n 1,2, ,m. μ λ m n ! m! μ λ m m 1 m n 1 μ m n 1 λ m n 2 λ m 1 λ mλ n n n = − = − − + = − + − + − = 当 n n-1 1 n - 1 n - 2 0 μμ μ λ λ λ Cn =0 , 当n>m 于是,P0= ( ) − = = = m n 0 n μ λ m n! m! 1 n 0 Cn 1 Pn = CnP0= 0 n=1,2, …, m n P μ λ m n! m! − (m-2)λ