
§40一1型整数规划 0一1型整数规划是整数规划的特殊情形,它的决策变量 仅取0或1这两个值,这时的决策变量也称为0一1变量。在实 际问题中,有些问题只需回答“是”或“否”,问题就解决 了,描述这类问题的变量只需取两个值就可以了。例如是否 采纳某个方案;某项任务是否可以交某人承担;集装箱内是 否装入某种货物等等。对于这类问题我们可以用逻辑变量来 描述: 1,是 X= 0,否
§4 0—1 型整数规划 0—1 型整数规划是整数规划的特殊情形,它的决策变量 仅取0或1这两个值,这时的决策变量也称为0—1 变量。在实 际问题中,有些问题只需回答“是”或“否”,问题就解决 了,描述这类问题的变量只需取两个值就可以了。例如是否 采纳某个方案;某项任务是否可以交某人承担;集装箱内是 否装入某种货物等等。对于这类问题我们可以用逻辑变量来 描述: = 否 是 , , 0 1 x

4.1引入0一1变量的实例 1.确定投资方案 相互排斥的计划 例4某市工商银行拟抽调a万元资金对小五金、小百货和洗 涤剂三个行业给予低息贷款。由于资金有限,只能在四个小五金 企业A、A、A、A中至多选两个;在五个小百货企业A、A6 A、A中至多选三个;在四个洗涤剂企业A,、A1o、A1、A12中 至多选两个给予低息贷款。已知企业A得到贷款a万元后,可获 利b万元。问工商银行应如何发放贷款,可使总利润最大? 解:因为本问题只要求解决是否给企业贷款,因此可用0一1 变量描述所求方案。设 1,给A贷款 0,不给4否贷款1=12,12 于是,根据题意, 本问题可描述为: max ≤2 盒xs2 X=0或1,=1,2,…,12
4.1 引入0—1 变量的实例 1.确定投资方案——相互排斥的计划 例4 某市工商银行拟抽调a万元资金对小五金、小百货和洗 涤剂三个行业给予低息贷款。由于资金有限,只能在四个小五金 企业A1、A2、A3、A4 中至多选两个;在五个小百货企业A5、A6、 A7、A8 中至多选三个;在四个洗涤剂企业A9、A10、A11、A12 中 至多选两个给予低息贷款。已知企业Ai得到贷款ai万元后,可获 利bi万元。问工商银行应如何发放贷款,可使总利润最大? 解:因为本问题只要求解决是否给企业贷款,因此可用0—1 变量描述所求方案。设 = , =1,2,,12 i 不给A否贷款 给A 贷款 , , 0 1 i i i x 于是,根据题意,本问题可描述为: maxZ= = 12 i 1 i i bx a x a i i i = 12 1 2 4 1 i= i x 3 9 5 i= i x 2 12 10 i= i x Xi=0或1,i=1,2, …,12

这是一个0一1整数规划问题。与其相类似的问题很多,比 如:投资项目的选择;投资场所的选定;工厂的选址;新产品 开发方案的确定等等。总之,凡是一些相互排斥的计划、方案 的确定问题都可以归结为与例4类似的0一1整数规划问题。 2.相互排斥的约束条件 回顾本章例1,用集装箱托运甲、乙两种货物,根据每件货 物的体积、重量、可获利润,以及集装箱的托运限制得整数规划 模型如下: (x1,2分别表示甲、乙货物托运的件数) maxZ=20x+10x2 (1) 5x1+4x2≤24 (2) 2x1+5x≤13 (3) X1,X2≥0,整数 (4) 今设集装箱有车运和船运两种方式,(3)式是车运时的重 量限制条件。如用船运时关于重量的限制条件为2x,+5x,≤20 试确定集装箱托运甲、乙货物的数量及运输方式,使总利润最大 为了建立问题的模型,除了设甲、乙货物托运的件数分别为 xx外,还要把运输方式表示出来。由于只有两种运输方式,所
这是一个0—1整数规划问题。与其相类似的问题很多,比 如:投资项目的选择;投资场所的选定;工厂的选址;新产品 开发方案的确定等等。总之,凡是一些相互排斥的计划、方案 的确定问题都可以归结为与例4 类似的0—1整数规划问题。 2.相互排斥的约束条件 回顾本章例1,用集装箱托运甲、乙两种货物,根据每件货 物的体积、重量、可获利润,以及集装箱的托运限制得整数规划 模型如下: (x1 ,x2分别表示甲、乙货物托运的件数) maxZ=20x1+10x2 ⑴ 5x1+4x2 ≤24 ⑵ 2x1+5x2 ≤13 ⑶ x1 ,x2 ≥0,整数 ⑷ 今设集装箱有车运和船运两种方式,(3)式是车运时的重 量限制条件。如用船运时关于重量的限制条件为 2x1+5x2 ≤20 试确定集装箱托运甲、乙货物的数量及运输方式,使总利润最大。 为了建立问题的模型,除了设甲、乙货物托运的件数分别为 x1 ,x2外,还要把运输方式表示出来。由于只有两种运输方式,所

以可设 1,车运 0,船运 在约束条件中,两种不同运输方式对应的重量约束条件是相互 排斥的,所以不能简单地将它们都写到约束中。利用y这个0一1 变量可以将上述两个重量约束改写成: 2x1+5x2≤13+(1-y)M (5) 2X,+5x,≤20+yM (6) 其中M是相当大正数,显然当y=1时,(⑤)式就是车运的重量限制 条件,而(6)式自然成立,因而是多余的;当y=O时,(6)式就是船 运的重量限制条件,而(⑤)式成为多余的。经过这样处理后,问 题的数学模型可以写成如下形式: maxZ=20x+10x2 5x1+4x,≤24 2x+5x,≤13+(1-y)M 2x+5x20+yM X1,X2≥0,整数 y=0或1
以可设 = 船运 车运 , , 0 1 y 在约束条件中,两种不同运输方式对应的重量约束条件是相互 排斥的,所以不能简单地将它们都写到约束中。利用y这个0—1 变量可以将上述两个重量约束改写成: 2x1+5x2 ≤13+(1-y)M ⑸ 2x1+5x2 ≤20+yM ⑹ 其中M是相当大正数,显然当y=1时,⑸式就是车运的重量限制 条件,而⑹式自然成立,因而是多余的;当y=0时,⑹式就是船 运的重量限制条件,而⑸式成为多余的。经过这样处理后,问 题的数学模型可以写成如下形式: maxZ=20x1+10x2 5x1+4x2 ≤24 2x1+5x2 ≤13+(1-y)M 2x1+5x2 ≤20+yM x1 ,x2 ≥0,整数 y=0或1

类似地,如果有m个相互排斥的约束条件: ai1x1tai2x2+·…+ainXn≤b1 (i=1,2,m) 为了保证这m个条件只有一个起作用,可以引入m个0一1变 量y1(i=1,2,m)和充分大正常数M,将这个约束条件改写成: aiix1+ai2x2+…+ainXni≤b:+yiM (i=1,2,.m) y1+y2+.+ym-=m-1 显然,这些y:中只能有一个取0值,因而这个约束只能有一个 起作用,而其余都是多余的
类似地,如果有m个相互排斥的约束条件: ai1x1 +ai2x2 +‥‥+ainxn≤bi (i=1,2,…m) 为了保证这m个条件只有一个起作用,可以引入m个0—1变 量 yi(i=1,2,…m)和充分大正常数M,将这个约束条件改写成: ai1x1 +ai2x2 +‥‥+ainxn≤bi+yiM (i=1,2,…m) y1 +y2 +…+ym =m-1 显然,这些yi中只能有一个取0值,因而这m个约束只能有一个 起作用,而其余都是多余的

4.20一1型整数规划的解法 对于0一1型整数规划的求解问题,由于每个变量只取0、1两 个值,人们自然会想到用穷举法来求解,即排出变量取值为0或1 的每一种组合(共2个点),验证它们是否满足约束条件,再算 出每个可行解的目标函数值,比较各函数值以求得最优解。显然 当n较大时,计算量是相当大的。(如210=1024)因此,常设计一 些方法,只检查变量取值组合的一部分,就能求得问题的最优解。 这一类方法称为隐枚举法。 为了便于应用隐枚举法,当目标函数要求极大值时,可先将 0一1型整数规划中变量x,的顺序重新排列,使x,在目标函数中的 系数呈递增(不减)的,并且按二进制数码从小到大的顺序排列 每一组解,即按(00..00)、(00..01)、(00.10).(11..11) 的顺序排列。这样,可使最优解容易比较早地发现,使得计算简 化。 下面举例说明如何运用隐枚举法求解0一1型整数规划
4.2 0—1 型整数规划的解法 对于0—1 型整数规划的求解问题,由于每个变量只取0、1两 个值,人们自然会想到用穷举法来求解,即排出变量取值为0或1 的每一种组合(共2 n个点) ,验证它们是否满足约束条件,再算 出每个可行解的目标函数值,比较各函数值以求得最优解。显然 当n较大时,计算量是相当大的。(如2 10=1024)因此,常设计一 些方法,只检查变量取值组合的一部分,就能求得问题的最优解。 这一类方法称为隐枚举法。 为了便于应用隐枚举法,当目标函数要求极大值时,可先将 0—1型整数规划中变量xi的顺序重新排列,使xi在目标函数中的 系数呈递增(不减)的,并且按二进制数码从小到大的顺序排列 每一组解,即按(00…00)、(00…01)、(00…10)…(11…11) 的顺序排列。这样,可使最优解容易比较早地发现,使得计算简 化。 下面举例说明如何运用隐枚举法求解0—1 型整数规划
例5求解 maxZ=3x-2x,+5x2 解:调整x,x,的顺序,使目标函数 X1+2x2X3≤2 中变量的系数呈递增(不减)的顺 X1+4x2+x3≤4 序,则问题变为: X1+X2 ≤3 maxZ--2x+3x+5x3 4X2+x3≤6 2X2+X1X3≤2 ① X1,x2,x3=0或1 4x2+x1+x3≤4 ② 解 约束条件 X2+x1 S3 ③ ④ (X2X1,Xg) ① ②③④ 4X2 +x3≤6 值 X1X2,X3=0或1 (000) 0 按二进制数码从小到大的顺序排列 (001) 5 并检查各个解,先计算解的目标值 (010) 若目标值小于目前可行解最好的目 (011) 8 标值,则不必检查是否满足约束条 (100) 件,当所有解被检查完毕,就可判 (101) 断出最优解。计算结果可列表表示 (110) 见左表。最终得到最优解:X=1, (111) 6 x20,x3=1,最优值:Z=8
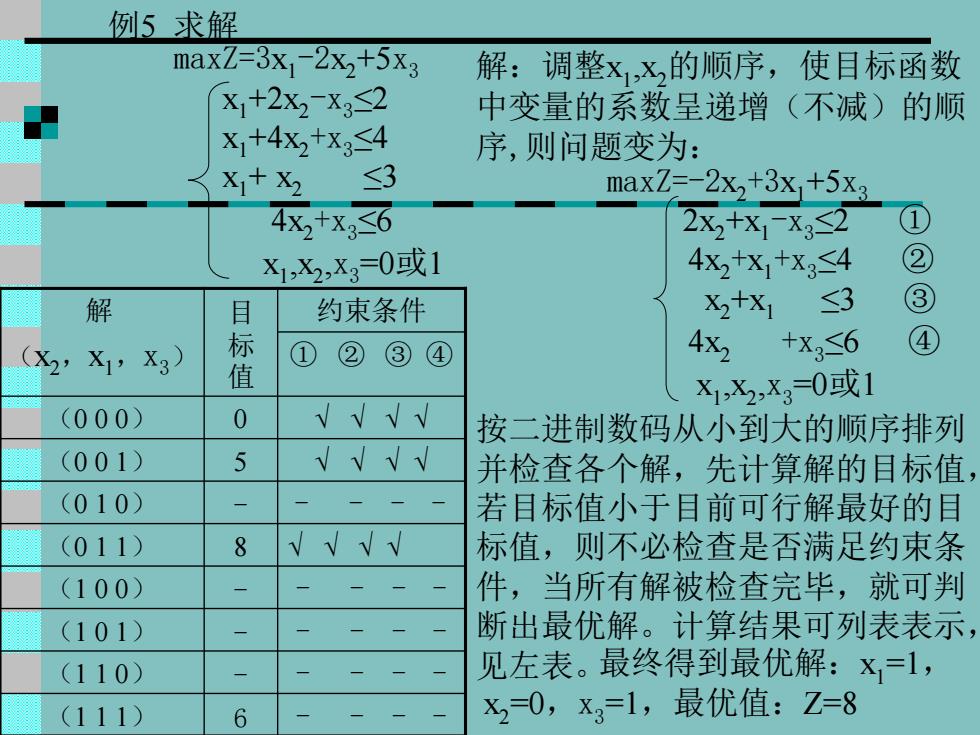
例5 求解 maxZ=3x1 -2x2+5x3 x1+2x2 -x3 ≤2 x1+4x2 +x3 ≤4 x1+ x2 ≤3 4x2 +x3 ≤6 x1 ,x2 ,x3 =0或1 解:调整x1 ,x2的顺序,使目标函数 中变量的系数呈递增(不减)的顺 序,则问题变为: maxZ=-2x2 +3x1+5x3 2x2+x1 -x3 ≤2 ① 4x2 +x1 +x3 ≤4 ② x2+x1 ≤3 ③ 4x2 +x3 ≤6 ④ x1 ,x2 ,x3 =0或1 按二进制数码从小到大的顺序排列 并检查各个解,先计算解的目标值, 若目标值小于目前可行解最好的目 标值,则不必检查是否满足约束条 件,当所有解被检查完毕,就可判 断出最优解。计算结果可列表表示, 见左表。 解 (x2,x1,x3) 目 标 值 约束条件 ① ② ③ ④ (0 0 0) 0 √ √ √ √ (0 0 1) 5 √ √ √ √ (0 1 0) - - - - - (0 1 1) 8 √ √ √ √ (1 0 0) - - - - - (1 0 1) - - - - - (1 1 0) - - - - - (1 1 1) 6 - - - - 最终得到最优解:x1=1, x2=0,x3=1,最优值:Z=8