
§2动态规划的最优性原理 多阶段决策过程的特点是每个阶段都要进行决策,具有 个阶段的决策过程的策略是由个相继进行的阶段决策构成的 决策序列。由于前阶段的终止状态又是后一阶段的初始状态, 因此确定阶段最优决策不能只从本阶段的效应出发,必须通盘 考虑,整体规划。就是说,阶段k的最优决策不应只是本阶段 的最优,而必须是本阶段及其所有后续阶段的总体最优,即关 于整个后部子过程的最优决策。 对此,贝尔曼在深入研究的基础上,针对具有无后效性的 多阶段决策过程的特点,提出了著名的多阶段决策的最优性原 理: “整个过程的最优策略具有这样的性质:即无论过程过去 的状态和决策如何,对前面的决策所形成的状态而言,余下的 诸决策必须构成最优策略。’ 简而言之,最优性原理的含意就是:最优策略的任何一部 分子策略也必须是最优的
§2 动态规划的最优性原理 多阶段决策过程的特点是每个阶段都要进行决策,具有n 个阶段的决策过程的策略是由n个相继进行的阶段决策构成的 决策序列。由于前阶段的终止状态又是后一阶段的初始状态, 因此确定阶段最优决策不能只从本阶段的效应出发,必须通盘 考虑,整体规划。就是说,阶段k的最优决策不应只是本阶段 的最优,而必须是本阶段及其所有后续阶段的总体最优,即关 于整个后部子过程的最优决策。 对此,贝尔曼在深入研究的基础上,针对具有无后效性的 多阶段决策过程的特点,提出了著名的多阶段决策的最优性原 理: “整个过程的最优策略具有这样的性质:即无论过程过去 的状态和决策如何,对前面的决策所形成的状态而言,余下的 诸决策必须构成最优策略。” 简而言之,最优性原理的含意就是:最优策略的任何一部 分子策略也必须是最优的

如例1,A一B2一C1一D2一E是由A到E的最短路线,我们在 该路线上任取一点C,,按照最优性原理C,一D,一E应该是C,到 E的最短路。很容易用反证法证明这一结论的正确性,从而说 明最优性原理的正确性。 按最优性原理,·可以将例1分成AB二C一—D二E个阶段, 由后向前逐步求出各点到E的最短线路,直至求出A至E的最短 线路。 K=4时,出发点有D1,D2,D3,记 例1的线路网络图: (D)(i=1,2,3)为D到E的最短距 4(D)表示从状态D出发采取的决 策。显然:(D1)=7,u4(D)=E f(D2)=8,u4(D2)=E f(D3)=6,u4(D3)=E 9 K=3时,出发点有C1,C2,C3 (C)=min {d (C D)(D),d (C D2)(D2)) =min{4+7,2+8}=10, u3(C1)=D2 5(C2) =min {d (C2D2)(D2),d (C2D3)(D3) =min{5+8,7+6}=13, u3(C2=D2或D3 5(C3)=min{d(C3D2)+i(D2),d(C3D3)+f(D3)) =min{10+8,9+6}=15, u3(C3)=D3
如例1,A—B2—C1—D2—E是由A到E的最短路线,我们在 该路线上任取一点C1 ,按照最优性原理C1—D2—E应该是C1到 E的最短路。很容易用反证法证明这一结论的正确性,从而说 明最优性原理的正确性。 按最优性原理,可以将例1分成A—B—C—D—E 4个阶段, 由后向前逐步求出各点到E的最短线路,直至求出A至E的最短 线路。 K=4时,出发点有D1,D2,D3,记 f4(Di)(i=1,2,3)为Di到E的最短距 离;u4 (Di )表示从状态Di出发采取的决 策。显然: f4(D1)=7,u4 (D1 )=E f4(D2)=8,u4 (D2 )=E f4(D3)=6,u4 (D3 )=E K=3时,出发点有C1,C2,C3 f3(C1)=min{d(C1D1)+f4(D1),d(C1D2)+f4(D2)} =min{4+7,2+8}=10, u3 (C1 )= D2 f3(C2)=min{d(C2D2)+f4(D2),d(C2D3)+f4(D3)} =min{5+8,7+6}=13, u3 (C2 )= D2或D3 f3(C3)=min{d(C3D2)+f4(D2),d(C3D3)+f4(D3)} =min{10+8,9+6}=15, u3 (C3 )= D3
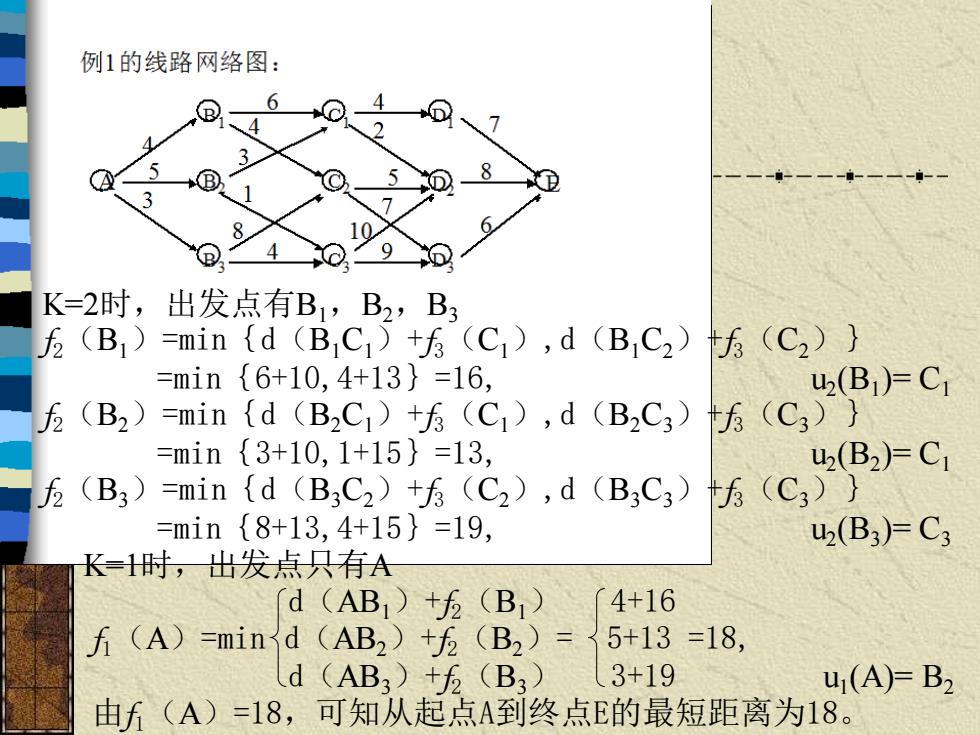
例1的线路网络图: 8 10 4 ,9 K=2时,出发点有B1,B2,B3 5(B)=min{d(BC1)+5(C),d(BC2)5(C2)) =min{6+10,4+13}=16, u2(B1)=C1 5(B2)=min{d(B,C)+5(C,),d(B,C3)5(C)) =min{3+10,1+15}=13, u2(B2=C1 5(B3)=min{d(B,C2)+5(C2),d(B,C3)5(C3)) =min{8+13,4+15}=19, 2(B3)=C3 K=时,出发点只有A d(AB1)+5(B1) 4+16 f(A)=min d (AB2)f (B2) 5+13=18, d (AB3)+5(B3) 3+19 1(A)=B2 由f(A)=18,可知从起点A到终点E的最短距离为18
K=2时,出发点有B1,B2,B3 f2(B1)=min{d(B1C1)+f3(C1),d(B1C2)+f3(C2)} =min{6+10,4+13}=16, u2 (B1 )= C1 f2(B2)=min{d(B2C1)+f3(C1),d(B2C3)+f3(C3)} =min{3+10,1+15}=13, u2 (B2 )= C1 f2(B3)=min{d(B3C2)+f3(C2),d(B3C3)+f3(C3)} =min{8+13,4+15}=19, u2 (B3 )= C3 K=1时,出发点只有A d(AB1)+f2(B1) 4+16 f1(A)=min d(AB2)+f2(B2)= 5+13 =18, d(AB3)+f2(B3) 3+19 u1 (A)= B2 由f1(A)=18,可知从起点A到终点E的最短距离为18

为了找出最短线路,再按计算顺序反推回去,可求出最优 决策序列,即由 uj(A)=B2,u(B2)C,Ug(C)=D2,u(D2)=E 组成最优策略,也就是最短线路为: A二B2二CD2二E 从上面的例子不难看出,对于最短线路问题,有如下的递 推关系(函数方程): 人(xk)=min{d(Xku()+f+1(T(xk,u)) f+1(Xt1)=0 k=n,n-1,.,1 一般情况下,多阶段决策问题存在下面的递推关系: (Xk)=opt rk(xk uk(x))*(T(xk uk)) u4∈Dk(u) +1(Xt1)=C k=n,n-1,..,1 这里rk(X,(X)是第阶段采用u(X)决策产生的阶段效应: +1(x1)=C是边界条件;“*”号大多数情况下是 “+”号, 也可能是“×”号。称上述递推关系为动态规划的基本方程, 这个方程是最优化原理的具体表达形式
为了找出最短线路,再按计算顺序反推回去,可求出最优 决策序列,即由 u1 (A)= B2 ,u2 (B2 )= C1 ,u3 (C1 )= D2,u4 (D2 )=E 组成最优策略,也就是最短线路为: A—B2—C1—D2—E 从上面的例子不难看出,对于最短线路问题,有如下的递 推关系(函数方程): fk(xk)=min{d(xk ,uk (xk ))+fk+1(T(xk , uk ))} fn+1(xn+1)=0 k=n,n-1,…,1 一般情况下,多阶段决策问题存在下面的递推关系: fk(xk)= opt{ rk (xk , uk (xk ))﹡fk+1(T(xk , uk ))} uk∈ Dk (uk ) fn+1(xn+1)=C k=n,n-1,…,1 这里rk (xk , uk (xk ))是第阶段采用uk (xk )决策产生的阶段效应; fn+1(xn+1)=C是边界条件;“﹡”号大多数情况下是 “+”号, 也可能是“×”号。称上述递推关系为动态规划的基本方程, 这个方程是最优化原理的具体表达形式

在基本方程中,「(,),k+1=T()都是已知函数,最 优子策略人(xk)与+1(x1)之间是递推关系,要求出人(x 及(),需要先求出+1(x+1),这就决定了应用动态规划 基本方程求最优策略总是逆着阶段的顺序进行的。 另一方面,由于k+1阶段的状态xk+1=T(x,u)是由前面的状 态和决策所形成的,在计算+1(x+1)时还不能具体确定x+1 的,这就要求必须就k+1阶段的各个可能状态计算+1(X+1) 因此动态规划不但能求出整个问题的最优策略和最优目标值, 而且还能求出决策过程中所有可能状态的最优策略及最优目标 值
在基本方程中, rk (xk , uk ), xk+1=T(xk , uk )都是已知函数,最 优子策略fk(xk)与fk+1(xk+1)之间是递推关系,要求出fk(xk) 及uk (xk ),需要先求出fk+1(xk+1),这就决定了应用动态规划 基本方程求最优策略总是逆着阶段的顺序进行的。 另一方面,由于k+1阶段的状态xk+1=T(xk , uk )是由前面的状 态和决策所形成的,在计算fk+1(xk+1)时还不能具体确定xk+1 的,这就要求必须就k+1阶段的各个可能状态计算fk+1(xk+1), 因此动态规划不但能求出整个问题的最优策略和最优目标值, 而且还能求出决策过程中所有可能状态的最优策略及最优目标 值