
第三章运输问题 ◆§3产销不平衡的运输问题 前面讨论的运输问题的理论和方法,都是以产销平衡,即 a,=b 为前提的。但是在实际问题中产销往往是不平衡的。对于产销 不平衡的运输问题,可以把它们先转化成产销平衡问题,然后 再用表上作业法求解。 1.产大于销的情况,即a,>b 由于总产量大于总销量,就要考虑多余的物资在哪些产地就地 贮存问题。将各产地的仓库设成一个假想销地B+1, 该地总需 求量为 d坚-Fd 再令运价表中各地到虚设销地Bn+1的单位运价Cn+1=0,i=1,2.m 侧该问题就转化成一个产销平衡问题,可以用表上作业法求解 了。在最优解中,产地A到虚设销地Bn+1的运量实际上就是产 地A就地贮存的多余物资数量
第三章 运输问题 §3 产销不平衡的运输问题 前面讨论的运输问题的理论和方法,都是以产销平衡,即 为前提的。但是在实际问题中产销往往是不平衡的。对于产销 不平衡的运输问题,可以把它们先转化成产销平衡问题,然后 再用表上作业法求解。 1.产大于销的情况,即 > 由于总产量大于总销量,就要考虑多余的物资在哪些产地就地 贮存问题。将各产地的仓库设成一个假想销地Bn+1,该地总需 求量为 再令运价表中各地到虚设销地Bn+1的单位运价Ci,n+1 =0,i=1,2…m, 则该问题就转化成一个产销平衡问题,可以用表上作业法求解 了。在最优解中,产地Ai到虚设销地Bn+1的运量实际上就是产 地Ai就地贮存的多余物资数量。 = = = n j 1 j m i 1 i a b = m i 1 i a = n j 1 j b − = = = + n 1 j j m 1 i i 1 n b a b
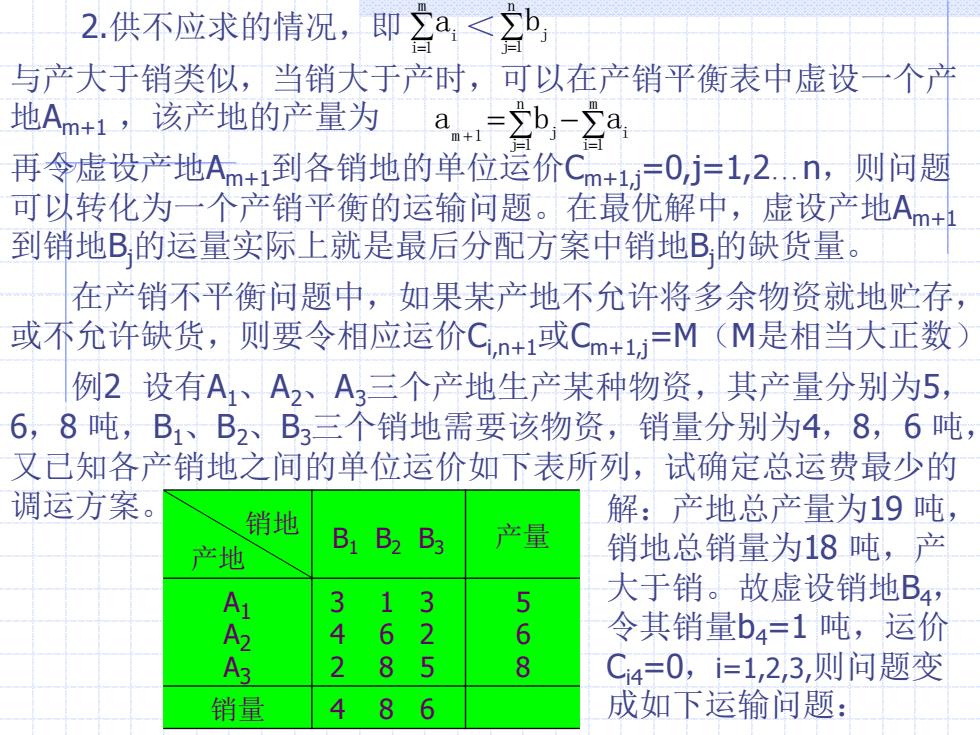
2.供不应求的情况,即a<b 与产大于销类似,当销大于产时,可以在产销平衡表中虚设一个产 地Am+1,该产地的产量为 a.-b-ga 再令虚设产地Am+1到各销地的单位运价Cm+1=0,j=1,2.n,则问题 可以转化为一个产销平衡的运输问题。在最优解中,虚设产地Am+ 到销地B,的运量实际上就是最后分配方案中销地B的缺货量。 在产销不平衡问题中,如果某产地不允许将多余物资就地贮存, 或不允许缺货,则要令相应运价Cin+1或Cm+1j=M(M是相当大正数) 例2设有A1、A2、A3三个产地生产某种物资,其产量分别为5, 6,8吨,B1、B2B3三个销地需要该物资,销量分别为4,8,6吨, 又已知各产销地之间的单位运价如下表所列,试确定总运费最少的 调运方案。 销地 解:产地总产量为19吨, 产地 B1 B2 B3 产量 销地总销量为18吨,产 3 1 3 5 大于销。故虚设销地B4, 4 6 2 6 令其销量b4=1吨,运价 3 2 8 5 8 C4=0,i=1,2,3,则问题变 销量 4 8 6 成如下运输问题:
2.供不应求的情况,即 < 与产大于销类似,当销大于产时,可以在产销平衡表中虚设一个产 地Am+1 ,该产地的产量为 再令虚设产地Am+1到各销地的单位运价Cm+1,j=0,j=1,2…n,则问题 可以转化为一个产销平衡的运输问题。在最优解中,虚设产地Am+1 到销地Bj的运量实际上就是最后分配方案中销地Bj的缺货量。 在产销不平衡问题中,如果某产地不允许将多余物资就地贮存, 或不允许缺货,则要令相应运价Ci,n+1或Cm+1,j=M(M是相当大正数) 例2 设有A1、A2、A3三个产地生产某种物资,其产量分别为5, 6,8 吨,B1、B2、B3三个销地需要该物资,销量分别为4,8,6 吨, 又已知各产销地之间的单位运价如下表所列,试确定总运费最少的 调运方案。 = m i 1 i a = n j 1 j b = − = = + m i 1 i n j 1 m 1 j a b a 销地 产地 B1 B2 B3 产量 A1 A2 A3 3 1 3 4 6 2 2 8 5 5 6 8 销量 4 8 6 解:产地总产量为19 吨, 销地总销量为18 吨,产 大于销。故虚设销地B4, 令其销量b4=1 吨,运价 Ci4=0,i=1,2,3,则问题变 成如下运输问题:
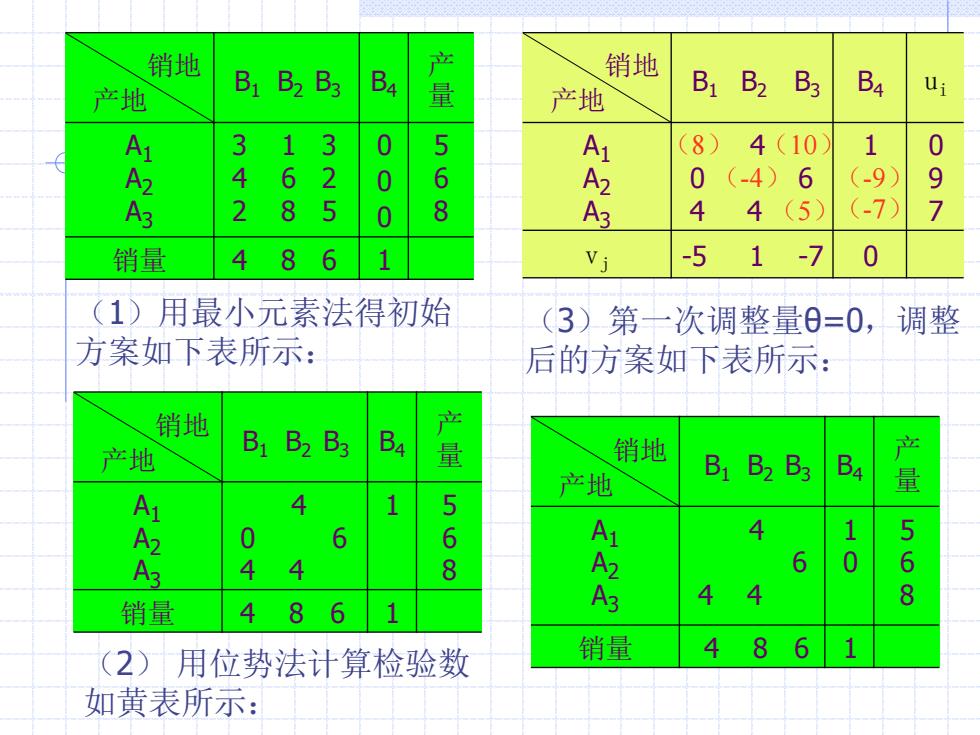
销地 B1 B2 B3 B4 销地 产地 量 产地 B1 B2 B3 B4 3 3 0 5 8) 4(10 1 0 A 4 6 2 0 6 0(-4) 6 (-9 9 2 8 5 0 8 3 4 4(5) -7) 7 销量 4 8 6 1 Vj 1 -7 0 (1)用最小元素法得初始 (3)第一次调整量0=0, 调整 方案如下表所示: 后的方案如下表所示: 销地 产地 B1 B2 B3 量 销地 产地 B1 B2 B3 B4 量 AL 4 1 0 6 6 1 4 5 A 4 6 0 6 A3 4 4 8 销量 4 86 (2)用位势法计算检验数 销量 4 8 6 如黄表所示:
销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 3 1 3 4 6 2 2 8 5 0 0 0 5 6 8 销量 4 8 6 1 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 4 0 6 4 4 1 5 6 8 销量 4 8 6 1 (1)用最小元素法得初始 方案如下表所示: (2) 用位势法计算检验数 如黄表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 4 0 6 4 4 1 0 9 7 vj -5 1 -7 0 (-7) (10) (-4) (-9) (8) (5) (3)第一次调整量θ=0,调整 后的方案如下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 4 6 4 4 1 0 5 6 8 销量 4 8 6 1
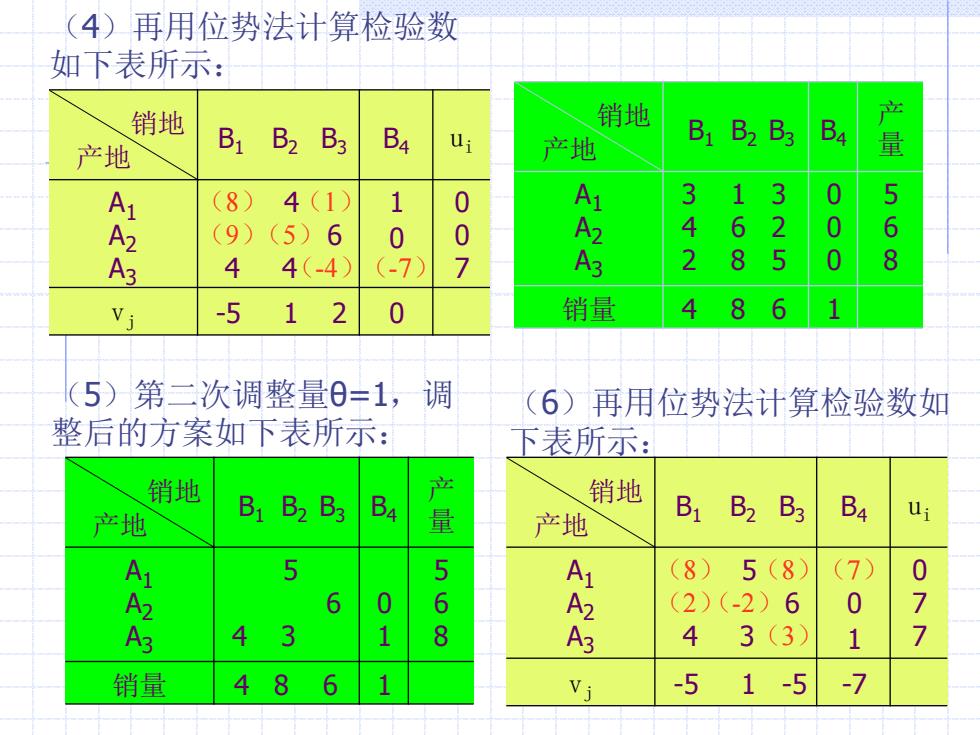
[4)再用位势法计算检验数 如下表所示: 销地 销地 立 产地 B1 B2 B3 B4 u Ba 产地 B1B2 B3 量 8) 4(1) 1 0 A1 3 1 3 0 5 (9)(5)6 0 0 4 6 2 A 68 4 4(-4》 (-7 7 2 8 5 0 Vj -5 12 0 销量 4 8 6 (5)第二次调整量0=1, 调 (6)再用位势法计算检验数如 整后的方案如下表所示: 下表所示: 销地 B1 B2 B3 产 销地 产地 产地 B1 B2 B3 B4 5 5 (8) 5(8) (7) 0 2 6 A2 (2)(-2)6 0 4 3 1 8 4 3(3) 1 销量 4 8 6 j -5 1-5 -7
(4)再用位势法计算检验数 如下表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 4 6 4 4 1 0 0 0 7 vj -5 1 2 0 (-4)(-7) (9) (8) (5) (1) 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 3 1 3 4 6 2 2 8 5 0 0 0 5 6 8 销量 4 8 6 1 (5)第二次调整量θ=1,调 整后的方案如下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 5 6 4 3 0 1 5 6 8 销量 4 8 6 1 (6)再用位势法计算检验数如 下表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 5 6 4 3 0 1 0 7 7 vj -5 1 -5 -7 (8) (8)(7) (2)(-2) (3)
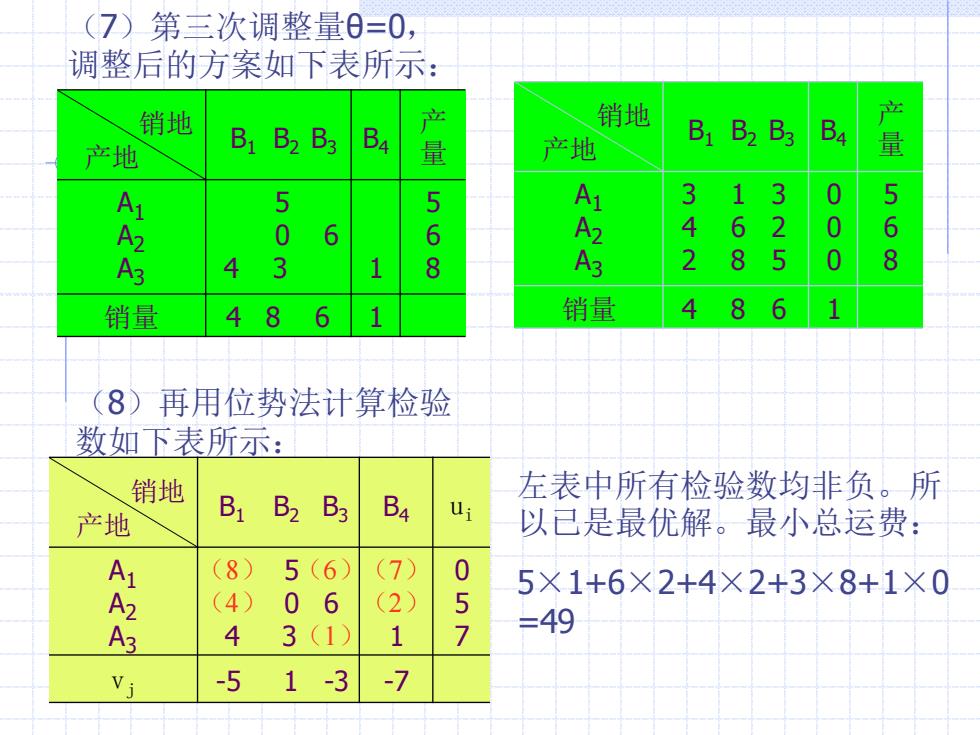
(7)第三次调整量0=0, 调整后的方案如下表所示: 销地 销地 产 产地 B1 B2 B3 产 B4 量 产地 B1 B2 B3 量 5 5 1 3 1 3 0 5 0 6 6 4 6 2 6 A 4 3 8 A3 2 8 5 0 8 销量 48 6 销量 4 8 6 (8)再用位势法计算检验 数如下表所示: 销地 左表中所有检验数均非负。所 产地 B1 B2 B3 B4 ui 以已是最优解。最小总运费: (8) 5(6)》 (7) 0 5×1+6×2+4×2+3×8+1×0 (4) 0. 6 (2) 5 3 4 3(1) 1 7 =49 -51 -3 7
(7)第三次调整量θ=0, 调整后的方案如下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 5 0 6 4 3 1 5 6 8 销量 4 8 6 1 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 3 1 3 4 6 2 2 8 5 0 0 0 5 6 8 销量 4 8 6 1 (8)再用位势法计算检验 数如下表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 5 0 6 4 3 1 0 5 7 vj -5 1 -3 -7 (8) (4) (6) (1) (7) (2) 左表中所有检验数均非负。所 以已是最优解。最小总运费: 5×1+6×2+4×2+3×8+1×0 =49

第三章作业 ◆P61:1.(1)、(2) ◆P62:2.(1)、(2)
第三章作业 P61:1. (1)、(2) P62:2. (1)、(2)