
§4对偶单纯形法 在单纯形法中,原问题的最优解满足: (1)是基本解; (2)可行(X.=Bb≥0); (3)检验数C-C.B1A≤0=YA≥C,即对偶解可行。 单纯形算法是从满足(1)、(2)的一个基可行解出发 转换到另一个基可行解,一直迭代到(3)得到满足,即 对偶解可行为止。而对偶单纯形法则是从满足(1) 、 (3)的一个对偶可行解出发,以基变量值是否全非负为 检验数,连续迭代到(2)得到满足,即原问题的基解可 行为止。两种算法结果是一样的,区别是对偶单纯形法 的初始解不一定可行,只要求所有检验数都非正,在保 证所得解始终是对偶可行解的前提下,连续迭代到原问 题的基解可行,丛而取得问题的最优解
•§4 对偶单纯形法 在单纯形法中,原问题的最优解满足: (1)是基本解; (2)可行( XB =B -1b≥0); (3)检验数C-CBB-1A≤0 YA≥C ,即对偶解可行。 单纯形算法是从满足(1)、(2)的一个基可行解出发, 转换到另一个基可行解,一直迭代到(3)得到满足,即 对偶解可行为止。而对偶单纯形法则是从满足(1)、 (3)的一个对偶可行解出发,以基变量值是否全非负为 检验数,连续迭代到(2)得到满足,即原问题的基解可 行为止。两种算法结果是一样的,区别是对偶单纯形法 的初始解不一定可行,只要求所有检验数都非正,在保 证所得解始终是对偶可行解的前提下,连续迭代到原问 题的基解可行,从而取得问题的最优解

对偶单纯形法计算步骤如下: 步骤1确定原问题(L)的初始基B,使所有检验 数o=C;-CBP,≤0,即Y=CB-1是对偶可行解,建立初 始单纯形表。 步骤2检查基变量的取值,若X=Bb≥0,则已得 最优解,计算停;否则求 min{(B-b);|(B-b):<0}=(B-b) 确定单纯形表第L行对应的基变量为旋出变量。 步骤3若所有a,≥0,则原问题无可行解,计算停; 否则,计算0=min{o;/aya,<0}=o/ak 确定对应的x为旋入变量。 步骤4以ak为主元作(L,K)旋转变换,得新的 单纯形表,转步骤2。 可以证明,按上述方法进行迭代,所得解始终是 对偶可行解
对偶单纯形法计算步骤如下: 步骤1 确定原问题(L)的初始基B,使所有检验 数 ,即Y=CBB-1是对偶可行解,建立初 始单纯形表。 步骤2 检查基变量的取值,若XB=B-1b≥0,则已得 最优解,计算停;否则求 min{(B-1b)i│(B -1b)i<0}=(B-1b)ι 确定单纯形表第L行对应的基变量为旋出变量。 步骤3 若所有aιj≥0,则原问题无可行解,计算停; 否则,计算 θ=min{σj / aιj│ aιj <0 }=σk /aιk 确定对应的xk为旋入变量。 步骤4 以aιk为主元作(L,K)旋转变换,得新的 单纯形表,转步骤2。 可以证明,按上述方法进行迭代,所得解始终是 对偶可行解。 σ C -C B P 0 j 1 j j B = −

例2用对偶单纯形法求解下述问题 minZ=12x1+8x2+16x3+12x4 2x1+2+4X3≥2 2x1+2x2+4X4≥3 X1,X2,X3,X4≥0 解:令Z=-Z,则问题可变为 max7=-12x1-8x2-16x3-12x4 -2x12-4X3 +X5 =-2 -2x1-2x2-4x4+x6-3 X1,X2,X3,X4,X5,X6≥0 取B=(P5,P6)为初始基,易见所有检验数σ≤0, 从而可建立单纯形表,计算结果如下:
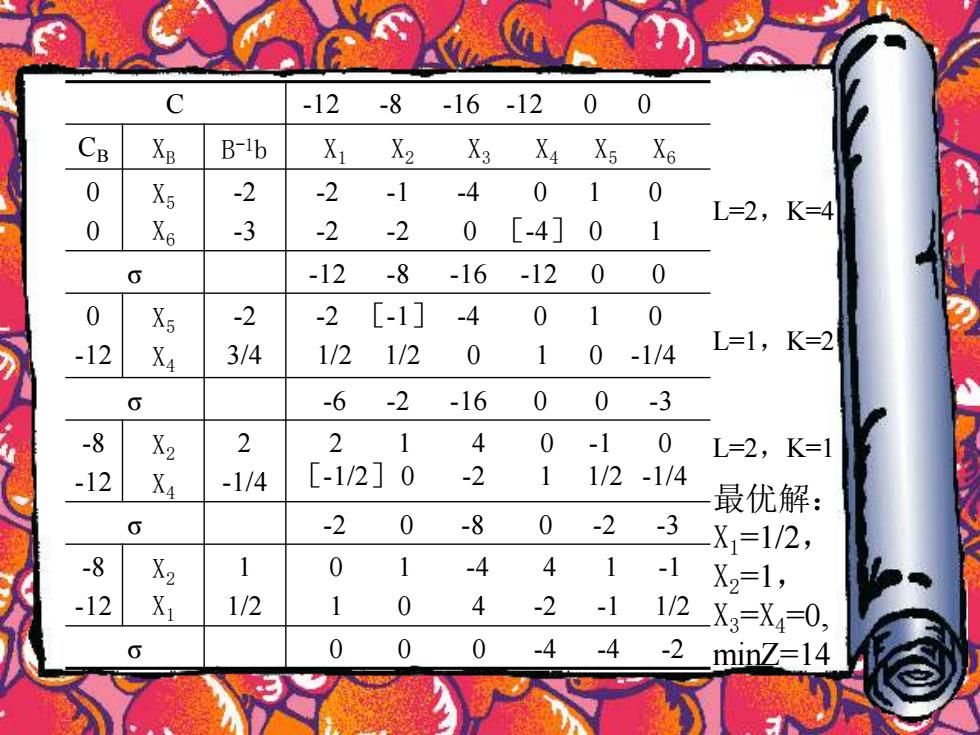
例2 用对偶单纯形法求解下述问题 minZ=12x1+8x2+16x3 +12x4 2x1+ x2 +4x3 ≥2 2x1+2x2+4x4 ≥3 x1 ,x2 ,x3 ,x4≥0 解:令 =-Z,则问题可变为 max =-12x1 -8x2 -16x3 -12x4 - 2x1 - x2 -4x3 +x5 =-2 -2x1 -2x2 -4x4 +x6 =-3 x1 ,x2 ,x3 ,x4 ,x5 ,x6≥0 取B=(P5,P6)为初始基,易见所有检验数σj≤0, 从而可建立单纯形表,计算结果如下: Z Z
C 12 -8 -16 -12 0 0 CB XB B-ib X X X3 X4 X5 X6 0 Xg -2 -2 -1 -4 0 1 0 L=2,K=4 0 -3 -2 -2 0[-4]01 G -12 -8 -16 -12 0 0 0 X5 -2 -2 [-1] -4 0 1 0 -12 X4 3/4 1/2 1/2 0 1 0-1/4 L=1,K=2 G -6 -2 -16 0 0 -3 -8 X2 2 2 1 4 0-1 0 L=2,K=1 -12 X4 -1/4 [-1/2]0 -2 11/2-1/4 最优解: 0 -2 0 -8 0 -2 -3 X1=1/2, -8 X2 1 0 -4 4 -1 X2=1, -12 1/2 0 4 -2 -1 1/2 X3=X40, -2 min☑14
C -12 -8 -16 -12 0 0 CB XB B -1b X1 X2 X3 X4 X5 X6 0 0 X5 X6 -2 -3 -2 -1 -4 0 1 0 -2 -2 0 [-4] 0 1 σ -12 -8 -16 -12 0 0 0 -12 X5 X4 -2 3/4 -2 [-1] -4 0 1 0 1/2 1/2 0 1 0 -1/4 σ -6 -2 -16 0 0 -3 -8 -12 X2 X4 2 -1/4 2 1 4 0 -1 0 [-1/2]0 -2 1 1/2 -1/4 σ -2 0 -8 0 -2 -3 -8 -12 X2 X1 1 1/2 0 1 -4 4 1 -1 1 0 4 -2 -1 1/2 σ 0 0 0 -4 -4 -2 L=2,K=4 L=1,K=2 L=2,K=1 最优解: X1=1/2, X2=1, X3=X4=0, minZ=14

本例如果用单纯形法计算,确定初始基可行解时 需引入两个人工变量,计算量要多于对偶单纯形法。 一般情况下,如果问题能够用对偶单纯形法计算,计 算量会少于单纯形法。但是,对偶单纯形法并不是一 种普遍算法,它有一定的局限性,不是任何线性规划 问题都能用对偶单纯形法计算的。当线性规划问题具 备下面条件时,可以用对偶单纯形法求解: ①问题标准化后,价值系数全非正; ②所有约束全是不等式
本例如果用单纯形法计算,确定初始基可行解时 需引入两个人工变量,计算量要多于对偶单纯形法。 一般情况下,如果问题能够用对偶单纯形法计算,计 算量会少于单纯形法。但是,对偶单纯形法并不是一 种普遍算法,它有一定的局限性,不是任何线性规划 问题都能用对偶单纯形法计算的。当线性规划问题具 备下面条件时,可以用对偶单纯形法求解: ①问题标准化后,价值系数全非正; ②所有约束全是不等式