
试卷代号:2320 座位号■■ 中央广播电视大学2012一2013学年度第二学期“开放专科”期末考试 物流管理定量分析基础试题 2013年7月 题 号 二 三 四 总 分 分数 得 分 评卷人 一、单项选择题(每小题4分,共20分) 1.某供求平衡运输问题有五个产地和四个销地,按最小元素法编制的初始调运方案中填 数字的格子数为()。 A.4 B.5 C.8 D.10 2.某物流公司有三种化学原料A1,A2,A3。每公斤原料A1含B1,B2,B3三种化学成分的含 量分别为0.7公斤、0.2公斤和0.1公斤,每公斤原料A2含B,B2,B的含量分别为0.1公斤、 0.3公斤和0.6公斤;每公斤原料A含B,B2,B的含量分别为0.3公斤、0.4公斤和0.3公斤。 每公斤原料A,A2,A,的成本分别为500元、300元和400元。今需要B:成分至少100公斤, B2成分至少50公斤,B成分至少80公斤。为列出使总成本最小的线性规划模型,设原料A, A2,A,的用量分别为x1公斤、x2公斤和x公斤,则化学成分B,应满足的约束条件为()。 A.0.2x1+0.3x2+0.4x3≥50 B.0.2x1+0.3x2+0.4.x3≤50 C.0.2x1+0.3x2+0.4x3=50 D.minS=500x1+300x2+400x3 3.用MATLAB软件将线性方程组的增广矩阵D化为行简化阶梯形矩阵的命令函数 为()。 A.rref(D) B.rref[D] C.rref(d) D.rrefD 1308
试卷代号 座位号 中央广播电视大学 2 0 3学年度第二学期"开放专科"期末考试 物流管理定量分析基础试题 2013 年7 |题号|一|二|三|四|总分! |分数 I I I I I |得分!评卷人| (每小题 4分,共 0分} I I I 1.某供求平衡运输问题有五个产地和四个销地,按最小元素法编制的初始调运方案中填 数字的格子数为( A.4 C.8 B.5 D.10 2. 有三种 原料 I ' 斤原 种化学成 量分别为 、0.2 和O. 含量 为0.1 0.3 和0.6 为0.3 、0.4 和0.3 每公斤原料 '岛,儿的成本分别为 0元、 0元和 0元。今需要 成 分 0公斤, 成分 斤9B 为列 成本最 ,A 成分 满足 束条 )。 A. O. 2X1+0. 3X2+0. 4X3~50 C. O. 2Xl +0. 3X2+0. 4X3= 50 B. O. 2Xl +0. 3X2+0. 4x3~50 D. minS=500x1 +300X2 十400X3 3. 用MATLAB软件 将 线 阵D 梯 形 为( )。 1308 A. rre f(D) C. rref(d) B. rref[D] D. rrefD

4.设某公司运输某物品的总成本(单位:百元)函数为C(g)=500+2g十g2,则运输该物品 的固定成本为( )百元。 A.202 B.500 C.107 D.10700 5.由曲线y=x3,直线x=1,x=2及x轴围成的曲边梯形的面积表示为()。 A.-frdr B.z'dz D. 得 分 评卷人 二、计算题(每小题7分,共21分) -1 0 2 17 6.已知矩阵A= -2 1 4 ,B=04 ,求:AB。 0 -2 3-1 7.设y=xe+,求y. 8.计算定积分:。(2-e)dx。 得 分 评卷人 三、编程题(每小题6分,共12分) 9.试写出用MATLAB软件计算函数y=er+2+Inz的二阶导数的命令语句。 1O,试写出用MATLAB软件计算不定积分2=三dz的命令语句。 得 分 评卷人 四、应用题(第11、12题各14分,第13题19分,共47分) 11.某企业按年度计划需要某种零件1200000件,已知每个零件每月库存费为0.02元,每 次订货费为160元,为节省总成本,分批订货,假定企业对该零件的使用是均匀的,试求经济 1309
4. 品 的 =500+2q+q2 的固定成本为( )百元。 A.202 C.I07 B.500 D.I0700 5. 边梯形 面积表示 )。 A. - f:x 3dx B. fX 3dx C. J: x 3 dx D. J: x 3 dx |得分|评卷人 11 每小 AB 14- B 91" -10 A 9" 定积分 (2 - e)dx |得分|评卷人| L I I 三、编程题(每小题 6分,共 2分) 9. 用MATLAB +歹 令语 10 用MATLAB 定积 得分|评卷人 四、应用题{第 1、 2题各 4分,第 3题 9分,共 7分) 1. 企业按 某种 件1200000 为0.02 次订货费为 0元,为节省总成本,分批订货,假定企业对该零件的使用是均匀的,试求经济 1309
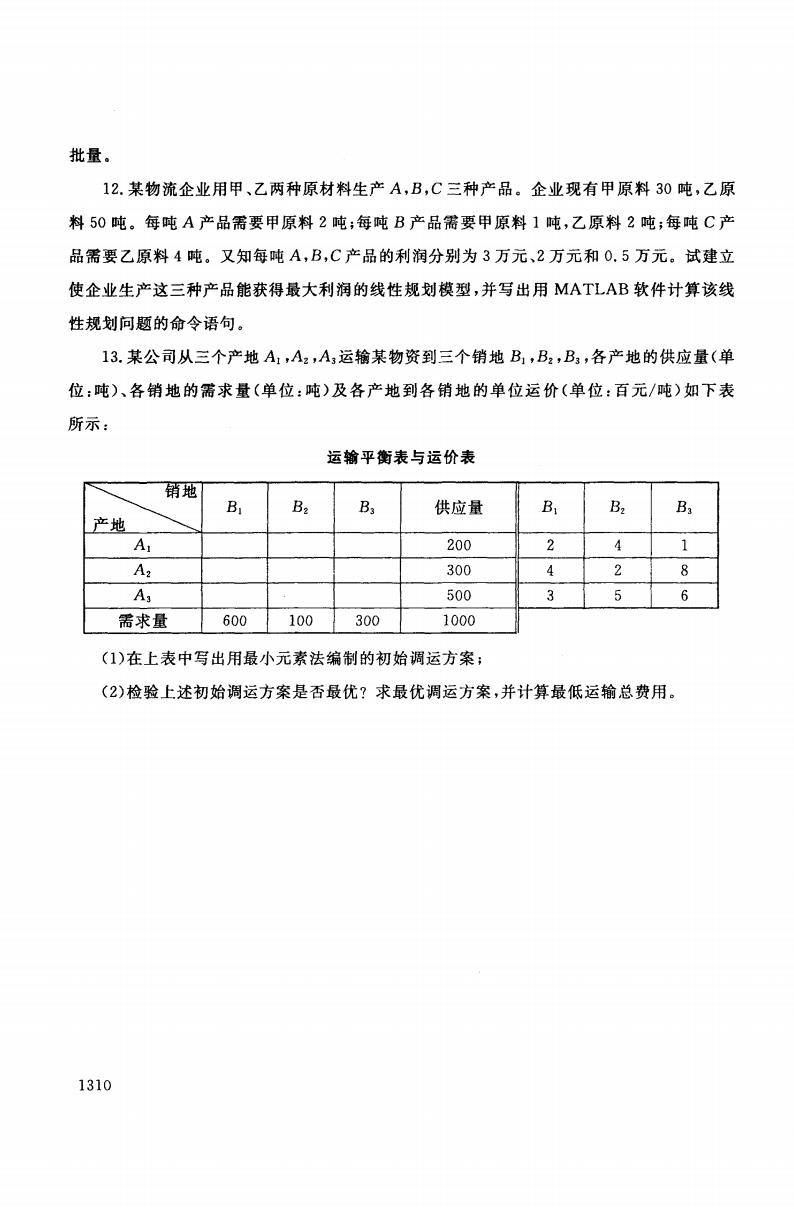
批量。 12.某物流企业用甲、乙两种原材料生产A,B,C三种产品。企业现有甲原料30吨,乙原 料50吨。每吨A产品需要甲原料2吨;每吨B产品需要甲原料1吨,乙原料2吨;每吨C产 品需要乙原料4吨。又知每吨A,B,C产品的利润分别为3万元、2万元和0.5万元。试建立 使企业生产这三种产品能获得最大利润的线性规划模型,并写出用MATLAB软件计算该线 性规划问题的命令语句。 13.某公司从三个产地A1,A2,A3运输某物资到三个销地B1,B2,B3,各产地的供应量(单 位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表 所示: 运输平衡表与运价表 销地 B Ba B3 供应量 B B2 Ba 产地 A 200 4 1 A2 300 4 2 8 A 500 3 5 6 需求量 600 100 300 1000 (1)在上表中写出用最小元素法编制的初始调运方案; (2)检验上述初始调运方案是否最优?求最优调运方案,并计算最低运输总费用。 1310
批量。 12. 企业现有 料30 0吨。每吨 A产品需要甲原料 2吨;每吨 B产品需要甲原料 1吨,乙原料 2吨;每吨 C产 品需要乙原料 4吨。又知每吨 C产品的利润分别为 3万元、 2万元和 5万元。试建立 使企业生产这三种产品能获得最大利润的线性规划模型,并写出用 B软件计算该线 性规划问题的命令语句。 13. 产地 各产地 供应 z吨〉、各销地的需求量(单位 z吨〉及各产地到各销地的单位运价(单位:百元/吨〉如下表 所示 运输平衡表与运价表 BI Bz B3 供应量 BI B2 B3 Al 200 2 4 1 A z 300 4 2 8 A 3 500 3 5 6 需求量 600 100 300 1000 (1) 用最 编制 初始 (2) 检验上述 求最优调运 算最低 1310

试卷代号:2320 中央广播电视大学2012一2013学年度第二学期“开放专科”期末考试 物流管理定量分析基础试题答案及评分标准 (供参考) 2013年7月 一、单项选择题(每小题4分,共20分) 1.C 2.A 3.A 4.B 5.D 二、计算题(每小题7分,共21分) [2-10]2 114 -21 6.AB= -21 4 04=8-2 7分 30-23-105 7.y=(x)'·e+x(e)'+()'=(1+x)e- 7分 8.2-e)dz=(2x-e)=3-e 7分 三、编程题(每小题6分,共12分) 9.>>clear >>syms x 2分 >>y=exp(-x)+(2+log(x)^(1/3); 4分 >>dy=diff(y,2) 6分 10.>>clear >>syms x 2分 >>y=(2-sgrt(x))/x43; 4分 >int(y) 6分 四、应用题(第11、12题各14分,第13题19分,共47分) 11.库存总成本函数为:C(g)=0.12g+192000000 8分 1311
试卷代号 2 3 2 中央广播电视大学 3学年度第二学期"开放专科"期末考试 物流管理定量分析基础试题答案及评分标准 〈供参考〉 2013 年7 -、单项选择题{每小题 4分,共 0分) I. e 2.A 3. A 4. B S.D 二、计算题(每小题 7分,共 1分} mwilMW|lu 14- -t|||Illi--J--5 Fhu AB 9" 7y'=ω· e-" +x · (eY+φ'= (1+x )e% Z 8·f:(2 矿)dx =3-e 三、编程题{每小题6分,共 2分} 9. »c1ear »syms x > >y= exp( - x) + (2+ log(x) 口/3); »dy=diff ,2) 10. »clear »syms x > >y= (2-sqrt(x))/x"'3; »int(y) 四、应用题(第 1、 2题各 4分,第 3题 9分,共 7分) 1. 成本 为:C(q)=0·12q+1920q 1311

令C(g)=0.12-19200000=0得定义域内的椎一驻点g=40000件。 12分 即经济批量为40000件。 14分 12.设生产A,B,C三种产品分别为x1吨、x2吨和x3吨,显然,x1,x2,x≥0。 1分 maxS=3x1+2x2+0.5x3 2x1十x2 ≤30 线性规划模型为: 2x2十4x1≤50 8分 x1,x2,x3≥0 计算该线性规划模型的MATLAB语句为: >>clear >>C=-[320.5]; >>A=[210:024幻; 10分 >>B=[3050]; >>LB=[000]; 12分 >>[X,fval]=linprog(C,A,B,[],],LB) 14分 13.用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 销地 B B2 B 供应量 B Ba B 产地 A 200 200 2 4 1 A2 100 100 100 300 4 2 8 A3 500 500 3 5 6 需求量 600 100 300 1000 12分 找空格对应的闭回路,计算检验数,直到出现负检验数: 入11=5,入12=9,132=4,A33=-1 14分 已出现负检验数,方案需要调整,调整量为0=100吨。 16分 1312
192000000 (q) =0.12-2=0 q 惟一 4000 0 。12 即经济批量为 00 12. 生产 种产 三0 maxS=3XI +2X2 +0. 5X3 (2XI +X2 ~30 线性规划模型为:~ 2X2+4X3~50 lXI' 计算该线性规划模型的 B语句为: »clear »c= [ 3 2 O. 5J; »A=[2 1 0;0 2 4J; »B=[30 50J; »LB=[O 0 0 ]; > >[X,fval] = linprog(C, A , ,LB) 13. 最小元 初始调 案如下 运输平衡表与运价表 10 12 14 泣了 B I B2 B3 供应量 B I B2 B3 Al 200 200 2 4 1 A 2 100 100 100 300 4 2 8 A 3 500 500 3 5 6 需求量 600 100 300 1000 12 找空格对应的闭回路,计算检验数,直到出现负检验数: All = ,λ12 =9 'A32 =4 'A33 =-1 已出现负检验数,方案需要调整,调整量为 0吨。 1312 14 16
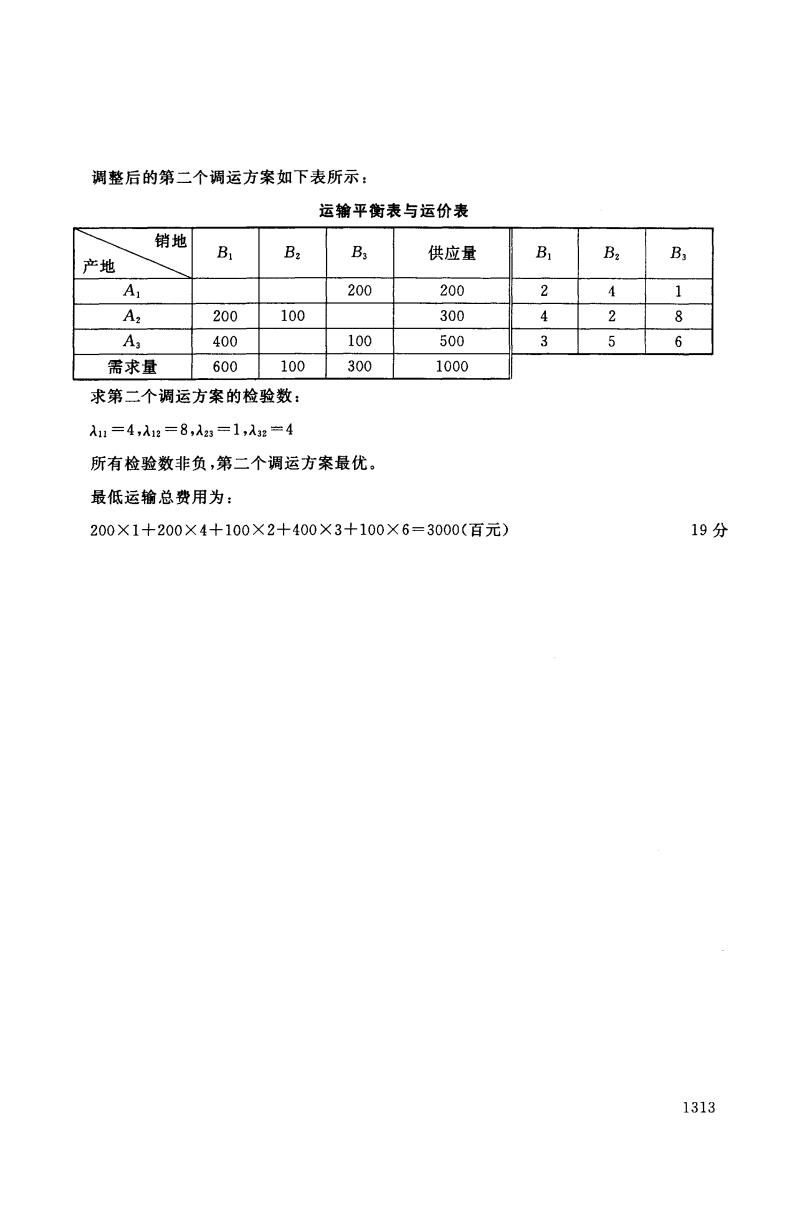
调整后的第二个调运方案如下表所示: 运输平衡表与运价表 销地 B B2 B 供应量 B Ba B 产地 A 200 200 2 4 1 A2 200 100 300 4 2 8 A 400 100 500 3 5 6 需求量 600 100 300 1000 求第二个调运方案的检验数: 入11=4,入12=8,λ23=1,入32=4 所有检验数非负,第二个调运方案最优。 最低运输总费用为: 200×1+200×4+100×2+400×3+100×6=3000(百元) 19分 1313
调整后的第二个调运方案如下表所示 运输平衡表与运价表 泣了 B1 Bz B3 供应量 B1 Bz B3 Al 200 200 2 4 1 Az 200 100 300 4 2 8 A 3 400 100 500 3 5 6 需求量 600 100 300 1000 求第二个调运方案的检验数: All =4 ,AIZ=8 ,Az3=1 ,,132 =4 所有检验数非负,第二个调运方案最优。 最低运输总费用为: 200X 1+200X 4+100 X 2+400X 3+100X 6=3000( 19 1313