
第十三章 回归与相关 第一节 直线回归 二、直线回归方程的求法 Y=a+bX 公式(13.1) b=>(X-XXY-Y)o 公式(13.2) ∑(X-X)2 a=Y-bX 公式(13.3) 例13.1 某研究者为探讨女性的年龄与收缩压的关系,收集了 某地12名妇女的年龄与收缩压数据见下表13-1的(2)、(3)。试求年龄与 收缩压的直线回归方程。 吉林大学远程教育学院
2 吉林大学远程教育学院 第十三章 回归与相关 第一节 直线回归 二、直线回归方程的求法 Y ˆ = a +bX 公式(13.1) XX XY l l X X X X Y Y b = − − − = 2 ( ) ( )( ) 公式(13.2) a = Y − bX 公式(13.3) 例13.1 某研究者为探讨女性的年龄与收缩压的关系,收集了 某地12名妇女的年龄与收缩压数据见下表13-1的(2)、(3)。试求年龄与 收缩压的直线回归方程
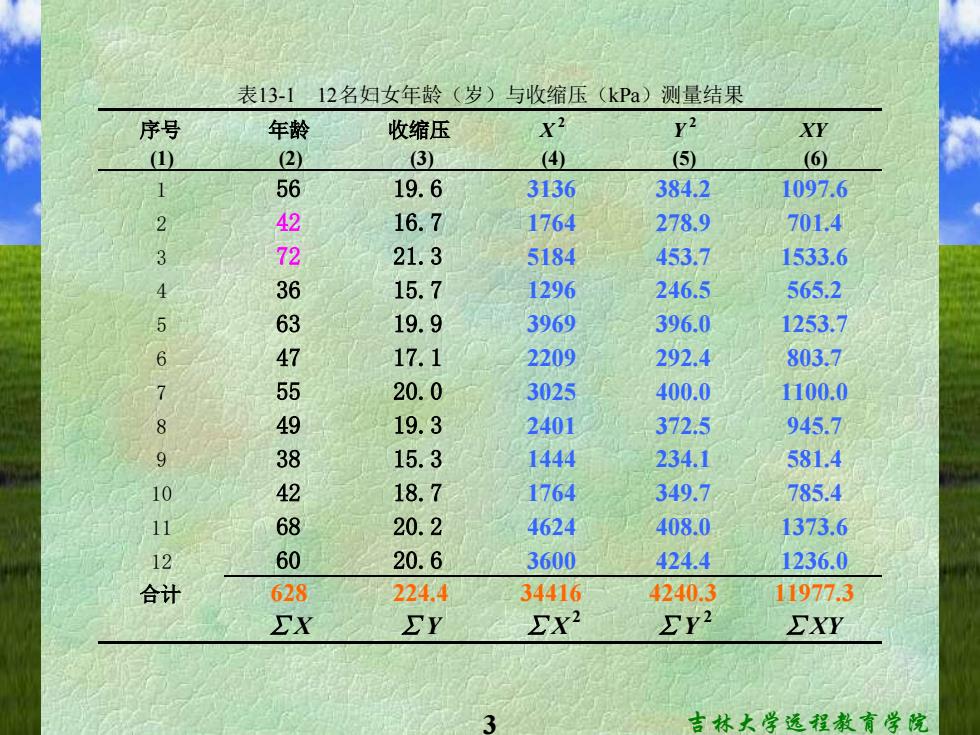
表13-112名妇女年龄(岁)与收缩压(kPa)测量结果 序号 年龄 收缩压 x2 Y2 XY (1) (2) (3) (4) (⑤) (6) 1 56 19.6 3136 384.2 1097.6 42 16.7 1764 278.9 701.4 72 21.3 5184 453.7 1533.6 4 36 15.7 1296 246.5 565.2 63 19.9 3969 396.0 1253.7 6 47 17.1 2209 292.4 803.7 55 20.0 3025 400.0 1100.0 P 49 19.3 2401 372.5 945.7 9 38 15.3 1444 234.1 581.4 10 42 18.7 1764 349.7 785.4 11 68 20.2 4624 408.0 1373.6 12 60 20.6 3600 424.4 1236.0 合计 628 224.4 34416 4240.3 11977.3 ∑X ∑Y EX2 ∑y2 ∑XY 3 吉林大学远程教育学院
3 吉林大学远程教育学院 序号 年龄 收缩压 X 2 Y 2 XY (1) (2) (3) (4) (5) (6) 1 56 19.6 3136 384.2 1097.6 2 42 16.7 1764 278.9 701.4 3 72 21.3 5184 453.7 1533.6 4 36 15.7 1296 246.5 565.2 5 63 19.9 3969 396.0 1253.7 6 47 17.1 2209 292.4 803.7 7 55 20.0 3025 400.0 1100.0 8 49 19.3 2401 372.5 945.7 9 38 15.3 1444 234.1 581.4 10 42 18.7 1764 349.7 785.4 11 68 20.2 4624 408.0 1373.6 12 60 20.6 3600 424.4 1236.0 合计 628 224.4 34416 4240.3 11977.3 ∑X ∑Y ∑X 2 ∑Y 2 ∑XY 表13-1 12名妇女年龄(岁)与收缩压(kPa)测量结果
L.先根据原始数据绘制散点图(scatter plot),大 致判断两变量之间是否有直线趋势 本例的散点图见下图13-1,可见年龄与收缩压 呈直线趋势,故可进行直线回归分析。 23 21 (ed) 17 ● 15 30 40 50 60 70 80 年龄(岁) 图13-112名妇女年龄与收缩压散点图 4 吉林大学远程教育学院
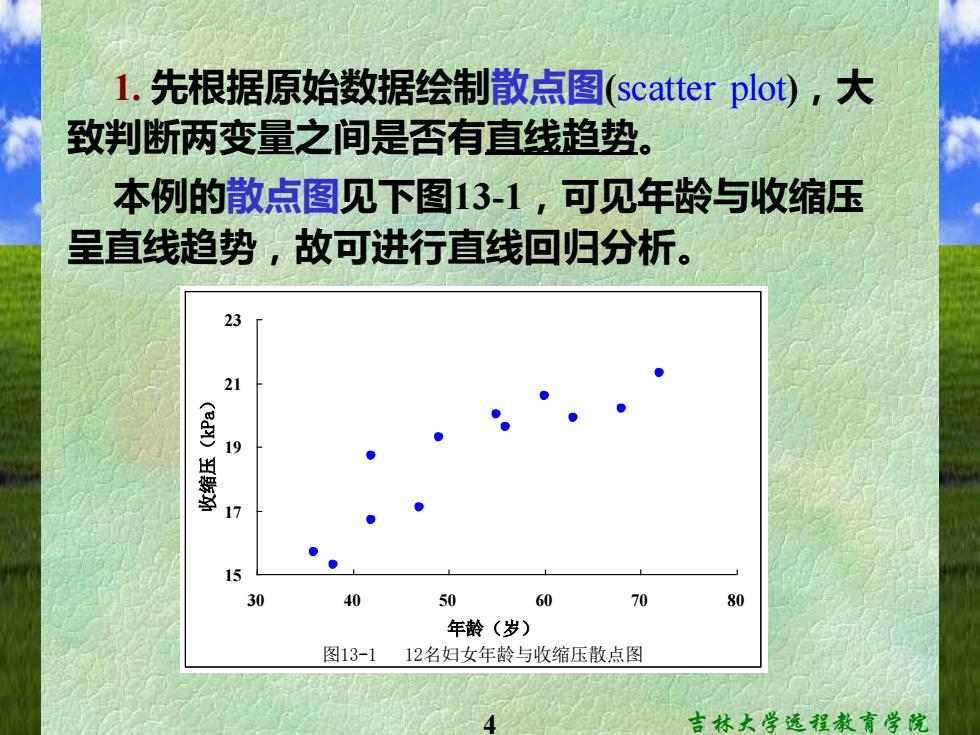
4 吉林大学远程教育学院 1. 先根据原始数据绘制散点图(scatter plot),大 致判断两变量之间是否有直线趋势。 本例的散点图见下图13-1,可见年龄与收缩压 呈直线趋势,故可进行直线回归分析。 图13-1 12名妇女年龄与收缩压散点图 15 17 19 21 23 30 40 50 60 70 80 年龄(岁) 收缩压(kPa)

2.计算∑x∑X、∑、∑2、∑XY 见表13 1中的2)(⑥合计项。 ∑X-=628,∑Y=224.4,∑X2=34416,∑P=4240.3,∑XY=11977.3 3.计算和风、1m1灯 x-∑X-28-523.y-∑y-244 n12 -18.7 n 2 a=∑(x-xy-Σx-②y-3416 6282 =1550.7 n 12 ,-∑w-)=∑r- =4240.3- 224.42 44.04 n 12 1-Σx-xxw-)=-Σx-∑X0∑2-11973- 28×224.4 12 -233.7 n 吉林大学远程教育学院
5 吉林大学远程教育学院 2. 计算∑X、∑Y、∑X2 、∑Y2 、∑XY 见表13- 1中的(2)~(6)合计项。 ∑X=628,∑Y=224.4,∑X 2=34416,∑Y 2 =4240.3,∑XY=11977.3 3. 计算 和lXX 、lYY、l X、Y XY 18.7 12 224.4 52.33 12 628 = = = = = = n Y Y n X X , = − = − = − =1550.7 12 628 34416 ( ) ( ) 2 2 2 2 n X l X X X X X = − = − = − = 44.04 12 224.4 4240.3 ( ) ( ) 2 2 2 2 n Y l YY Y Y Y = = − − = − = − 233.7 12 628 224.4 11977.3 ( )( ) ( )( ) n X Y l XY X X Y Y XY

4.求回归系数b和截距a」 按公式(13.2)求回归系 数b,按公式(13.3)求截距a。 b=lo 233.7 =0.1507 Ixx 1550.7 a=7-bx=18.7-0.1507×52.33=10.8139 5.列直线回归方程 =10.8139+0.1507X 为了直观分析或实际需要,可按求出的直线回 归方程作图。在X的实测全距范围内任取相距较远 且易读数的两个X值,代入方程得到两个值, 吉林大学远程教育学院
6 吉林大学远程教育学院 4. 求回归系数b和截距a 按公式(13.2)求回归系 数b,按公式(13.3)求截距a。 0.1507 1550.7 233.7 = = = X X X Y l l b a = Y −bX =18.7 − 0.150752.33 =10.8139 5. 列直线回归方程 Y ˆ =10.8139+0.1507X 为了直观分析或实际需要,可按求出的直线回 归方程作图。在X的实测全距范围内任取相距较远 且易读数的两个X值,代入方程得到两个Y值
以直线连接两点即得回归直线。本例可取X=42, 得Y=17.14;取X2=72,得Y2=21.66。连接两点即 得本资料的回归直线。见下图13-1a。 23 21 19 17 15 30 40 50 60 70 80 年龄(岁) 图13-1a 12名妇女年龄与收缩压散点图及回归直线 吉林大学远程教育学院
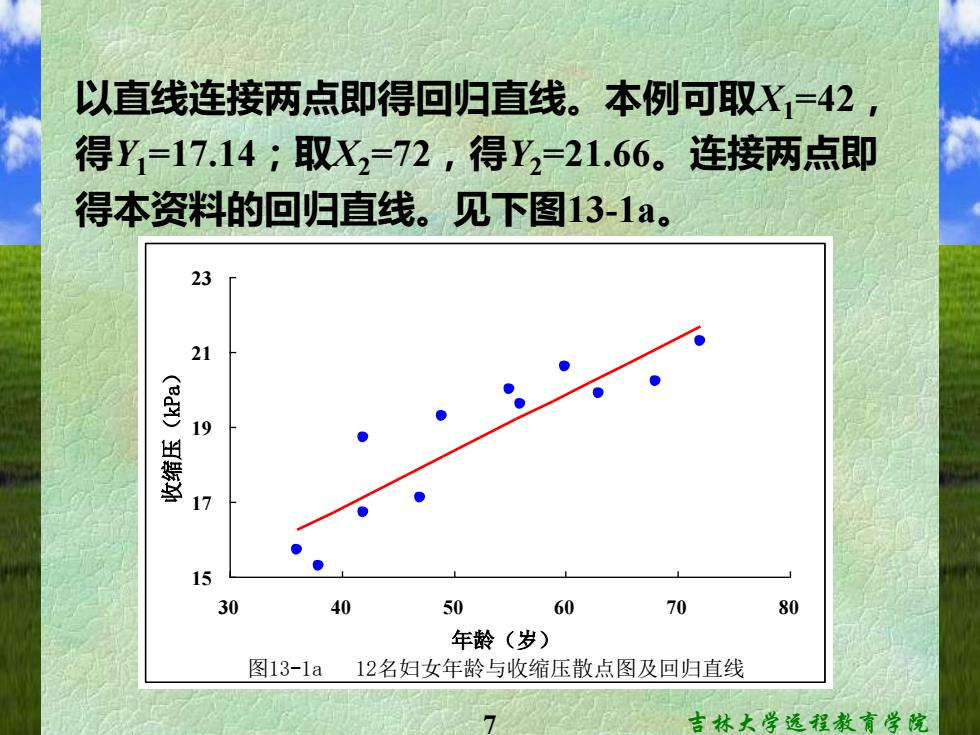
7 吉林大学远程教育学院 以直线连接两点即得回归直线。本例可取X1=42, 得Y1=17.14;取X2=72,得Y2=21.66。连接两点即 得本资料的回归直线。见下图13-1a。 图13-1a 12名妇女年龄与收缩压散点图及回归直线 15 17 19 21 23 30 40 50 60 70 80 年龄(岁) 收缩压(kPa)

三、回归系数的假设检验 我们知道即使X,的总体回归系数为零 由于抽样误差的存在,样本回归系数b也不一定为 零。因此需要对回归系数进行假设检验,以此推断 X,是否存在直线关系。可用方差分析或检验 (曰)方差分析 应变量的纵坐标被回归直线与均数截为三 段:第一段(Y-)表示P点与回归直线的纵向 距离,即实际值Y与估计值之差,称为剩余或 吉林大学远程教育学院
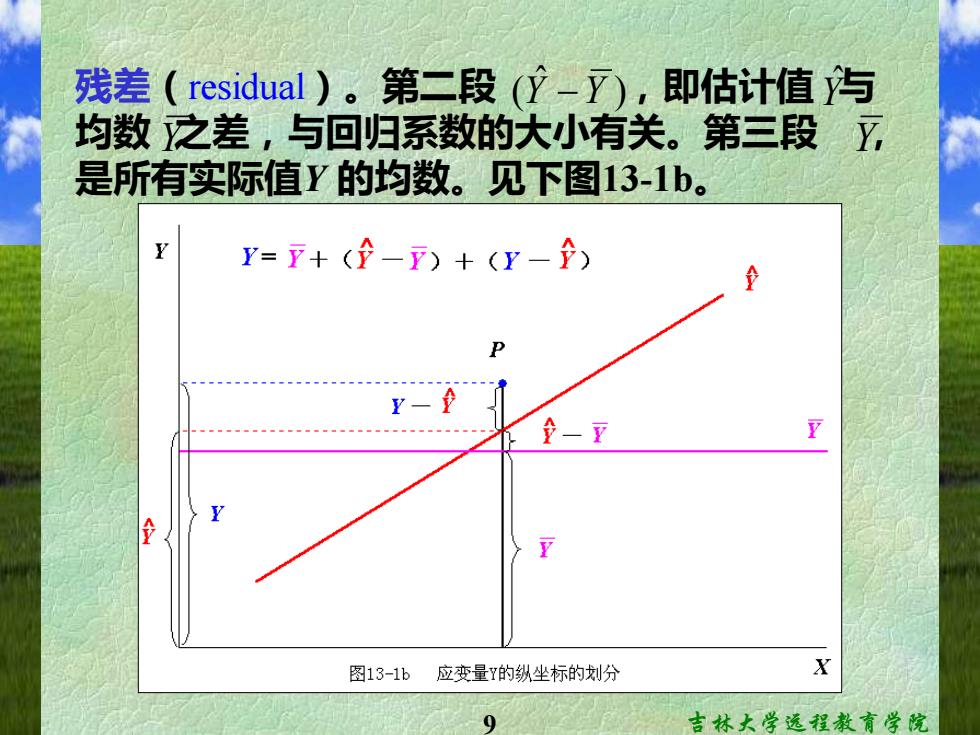
8 吉林大学远程教育学院 三、回归系数的假设检验 我们知道即使X、Y的总体回归系数β为零, 由于抽样误差的存在,样本回归系数b 也不一定为 零。因此需要对回归系数进行假设检验,以此推断 X、Y是否存在直线关系。可用方差分析或t 检验 。 ㈠ 方差分析 应变量Y的纵坐标被回归直线 与均数 截为三 段:第一段 ,表示P点与回归直线的纵向 距离,即实际值Y 与估计值 之差,称为剩余或 Y ˆ Y ) ˆ (Y −Y Y ˆ
残差(residual)。第二段(-7),即估计值泻 均数之差,与回归系数的大小有关。第三段7 是所有实际值Y的均数。见下图13-1b。 Y=F+(f-)+(y-) P 图13-1b 应变量Y的纵坐标的划分 X 吉林大学远程教育学院
9 吉林大学远程教育学院 残差(residual)。第二段 ,即估计值 与 均数 之差,与回归系数的大小有关。第三段 , 是所有实际值Y 的均数。见下图13-1b。 ) ˆ (Y −Y Y ˆ Y Y

从图13-1b中可以看出上述三段有下述关系: Y=7+(-T)+(Y-) 移项:y-了-(心-)+(Y-) 变换: ∑(Y-)=∑-)2+∑Y-) 上式用符号表示为:SS点=SS▣+SS利 式中SS总为的离均差平方和,反映的总变 异。SS回为回归平方和,反映在的总变异中由于 X与的直线关系而使的总变异减少的部分,即 在的总变异中可以用X解释的部分,SS回越大, 10 吉林大学远程教育学院
10 吉林大学远程教育学院 从图13-1b中可以看出上述三段有下述关系: ) ˆ ) ( ˆ Y = Y + (Y −Y + Y −Y 移项: ) ˆ ) ( ˆ Y −Y = (Y −Y + Y −Y 变换: − = − + − 2 2 2 ) ˆ ) ( ˆ (Y Y ) (Y Y Y Y 上式用符号表示为: SS总 = SS回 + SS剩 式中SS总为Y的离均差平方和,反映Y的总变 异。SS回为回归平方和,反映在Y的总变异中由于 X与Y的直线关系而使Y的总变异减少的部分,即 在Y的总变异中可以用X解释的部分,SS回越大

说明回归效果越好。SS剥为剩余平方和,反映X对 的线性影响之外的一切因素对的变异的作用, 即在的总变异中无法用X解释的部分,SS剩越小, 说明直线回归的估计误差越小。 自由度分别为:V总=n-1,响=1,剩=n-2 V总=回+蜊 sSa=1,=∑(W--∑y:- n 月 公式13.4 oxr SS剩=SS总-SS间 11 吉林大学远程教育学院
11 吉林大学远程教育学院 说明回归效果越好。SS剩为剩余平方和,反映X对 Y的线性影响之外的一切因素对Y的变异的作用, 即在Y的总变异中无法用X解释的部分,SS剩越小, 说明直线回归的估计误差越小。 自由度分别为:ν总= n-1,ν回= 1,ν剩= n-2 ν总 = ν回+ ν剩 = = − = − n Y SS l YY Y Y Y 2 2 2 ( ) 总 ( ) XX XY XY l l SS bl 2 回 = = SS剩 = SS总 − SS回 公式(13.4)