
第二节 集中趋势指标 二、几何均数 几何均数(geometric mean)用G表示。适用王 描述各观测值之间呈倍数送系(等比数列),或 偏态分布资料的变量值经对数变换后呈正态分布 (简称对数正态分布)资料的平均水平。 计算方法有: 1.直接法公式为: 吉林大学远程教育学院
2 吉林大学远程教育学院 二、几何均数 几何均数(geometric mean)用G表示。适用于 描述各观测值之间呈倍数关系(等比数列),或 偏态分布资料的变量值经对数变换后呈正态分布 (简称对数正态分布)资料的平均水平。 计算方法有: 第二节 集中趋势指标 1. 直接法 公式为:

G=WX,X2X,…X 公式(10.3) G-lg(BX)-g() 公式 n (10.4) 式中g表示lg的反函数,即lg1=10x。 例10.3现有7份血清的抗体效价为:1:2、1:4、1:8、1:32、 1:32、1:64、1:64。求其平均效价。 为简化计算,用抗体效价的倒数为X代入公式(10.4)得 G=gg2+g4+1g8++lg64)=g'1204=10≈16 7 该7份血清的平均抗体效价为1:16。 吉林大学远程教育学院
3 吉林大学远程教育学院 n G X X X Xn = 1 2 3 G X X X X n X n n = + + + + = − − lg ( lg lg lg ... lg ) lg ( lg ) 1 1 2 3 1 公式(10.3) 公式 (10.4) 例10.3 现有7份血清的抗体效价为:1:2、1:4、1:8、1:32、 1:32、1:64、1:64 。求其平均效价。 为简化计算,用抗体效价的倒数为X代入公式(10.4)得 : 式中lg-1表示lg 的反函数,即lg-1 =10x 。 ) lg (1.204) 10 16 7 lg 2 lg 4 lg 8 ... lg 64 lg ( 1 1 1.204 = = + + + + = − − G 该7份血清的平均抗体效价为1 : 16

2.加权法适合于有较多观测值或频数分布 表资料。公式为: G-lg(X+gx.+gX++.gX.) f+∫+f+.+f元 g 公式(10.5) 式中X是观测值或组中值。 例10.335名麻疹易感儿童接种麻疹疫苗一个月后,血凝抑 制抗体滴度见表10-3的(1)、(2)栏,求其平均滴度。 吉林大学远程教育学院
4 吉林大学远程教育学院 2. 加权法 适合于有较多观测值或频数分布 表资料。公式为: G f X f X f X f X f f f f n n n = + + + + + + + + − lg ( lg lg lg ... lg ... ) 1 1 1 2 2 3 3 1 2 3 = = − − lg ( lg ) lg ( lg ) 1 1 f X f f X n 公式(10.5) 式中X是观测值或组中值。 例10.3 35名麻疹易感儿童接种麻疹疫苗一个月后,血凝抑 制抗体滴度见表10-3的(1)、(2)栏,求其平均滴度
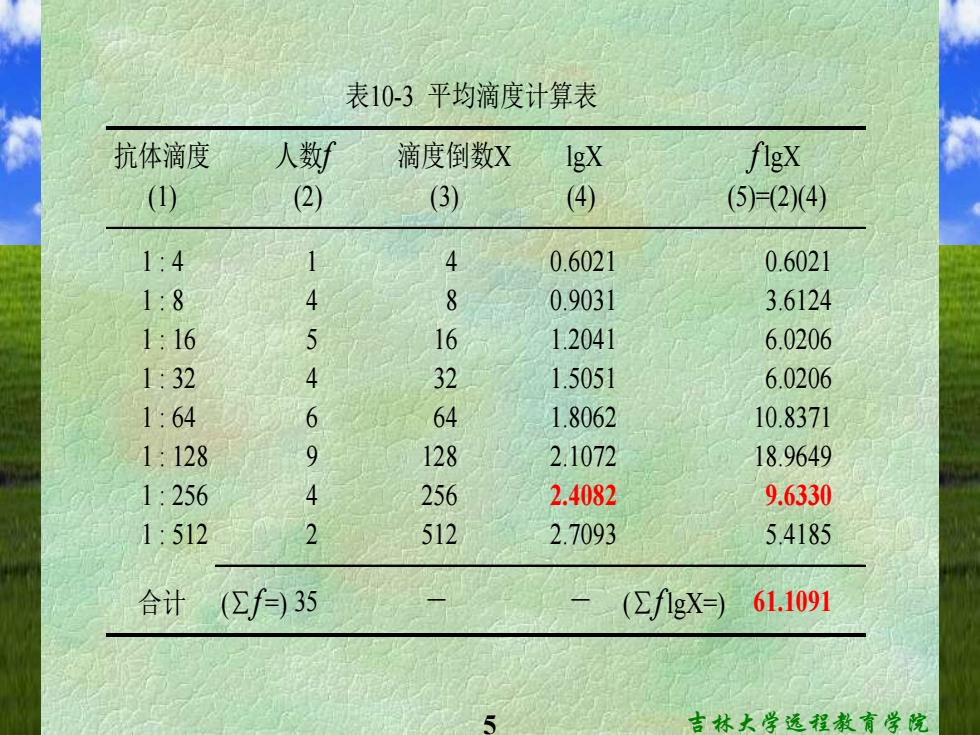
表10-3平均滴度计算表 抗体滴度 人数f 滴度倒数X IgX fIgX (I) 2) 3) (4) (5)=(24) 1:4 1 4 0.6021 0.6021 1:8 4 8 0.9031 3.6124 1:16 5 16 1.2041 6.0206 1:32 4 32 1.5051 6.0206 1:64 6 64 1.8062 10.8371 1:128 9 128 2.1072 18.9649 1:256 4 256 2.4082 9.6330 1:512 2 512 2.7093 5.4185 合计(Ef月)35 (Eflgx=) 61.1091 5 吉林大学远程教育学院
5 吉林大学远程教育学院 抗体滴度 人数f 滴度倒数X lgX f lgX (1) (2) (3) (4) (5)=(2)(4) 1 : 4 1 4 0.6021 0.6021 1 : 8 4 8 0.9031 3.6124 1 : 16 5 16 1.2041 6.0206 1 : 32 4 32 1.5051 6.0206 1 : 64 6 64 1.8062 10.8371 1 : 128 9 128 2.1072 18.9649 1 : 256 4 256 2.4082 9.6330 1 : 512 2 512 2.7093 5.4185 合计 (∑f =) 35 - - (∑f lgX=) 61.1091 表10-3 平均滴度计算表

代入公式(10.5)得: 0-业---00-g0460-s57 35名儿童接种麻疹疫苗后平均血凝抑制抗体滴度为1:55.7。 三、中位数 中位数(median)用M表示。一组观测值从小 到大顺序排列,位次居中的观测值即为中位数。 适用于各种资料,但常用于描述①偏态分布②分 布不清③有特大、特小值④端点无确定数值的资 料的集中位置。计算方法有: 吉林大学远程教育学院
6 吉林大学远程教育学院 代入公式(10.5)得: ) lg (1.7460) 55.7 35 61.1091 ) lg ( lg lg ( 1 1 1 = = = − − − f f X G 35名儿童接种麻疹疫苗后平均血凝抑制抗体滴度为 1 : 55.7。 三、中位数 中位数(median)用M表示。一组观测值从小 到大顺序排列,位次居中的观测值即为中位数。 适用于各种资料,但常用于描述①偏态分布②分 布不清③有特大、特小值④端点无确定数值的资 料的集中位置。 计算方法有:

1.直接法适合例数较少的资料。先将所有 观测值从小到大排序,当例数为奇数时,居中的 观测值即为中位数;当例数为偶数时,居中的两 个观测值相加除以2即为中位数。公式为: n为奇数时M=X 公式(10.6 n为偶数时 =Xg+x2 公式(10.7) 式中下标为排序后的观测值的位次。 吉林大学远程教育学院
7 吉林大学远程教育学院 1. 直接法 适合例数较少的资料。先将所有 观测值从小到大排序,当例数为奇数时,居中的 观测值即为中位数;当例数为偶数时,居中的两 个观测值相加除以2即为中位数。公式为: M = X n+ ( ) 1 2 M = X n + X n + [ ]/ 2 2 1 2 n为奇数时 n为偶数时 公式(10.6) 公式(10.7) 式中下标为排序后的观测值的位次

例10.5某传染病患者9例,他们的潜伏期分别为:6、5、 4、7、12、4、5、7、9天。求中位数。 首先排序:445567、7、9、12 位次:123456789 本例n=9为奇数,故M=6天。 用公式(106),M=X岁 =X=6(天) 例10.6若例10.5增加潜伏期为20天的一例。求中位数。 首先排序:4455617、9、12、20 位次:12345678910 本例n=10为偶数,故M=(6+7)/2=-6.5(天)。 用公式107),M-Xg:V2=x,+,)/2=6 吉林大学远程教育学院
8 吉林大学远程教育学院 例10.5 某传染病患者9例,他们的潜伏期分别为:6、5、 4、7、 12、 4、5、7、9天。求中位数。 首先排序:4、4、5、5、6、7、7、9、12 位次: 1 2 3 4 5 6 7 8 9 本例n=9为奇数,故M=6天。 用公式(10.6), 6( ) 5 ) 2 9 1 ( M = X + = X = 天 例10.6 若例10.5增加潜伏期为20天的一例。求中位数。 首先排序:4、4、5、5、6、7、7、9、12、20 位次: 1 2 3 4 5 6 7 8 9 10 本例n=10为偶数,故M=(6+7)/2=6.5(天)。 用公式(10.7), [ ]/ 2 ( )/ 2 6.5( ) 5 6 1 2 2 = + = + = 天 + M X n X n X X

2.频数分布表法适用于频数分布表资料。 公式为: M=L+ 公式(10.8) 式中L为中位数所在组段的下限;人M为该组段的频数: 为该组段的组距;为小于L的各组段累计频数。 要想判断出中位数所在组段,可从频数分布 表中先计算累计频数或累计频率,再利用/2或 50%找出中位数所在组段,最后代入公式(10.8)求 中位数。 吉林大学远程教育学院
9 吉林大学远程教育学院 2. 频数分布表法 适用于频数分布表资料。 公式为: ) 2 ( L M f n f i M = L + − 公式(10.8) 式中L为中位数所在组段的下限;fM为该组段的频数; i为该组段的组距;ΣfL为小于L的各组段累计频数。 要想判断出中位数所在组段,可从频数分布 表中先计算累计频数或累计频率,再利用n/2或 50%找出中位数所在组段,最后代入公式(10.8)求 中位数
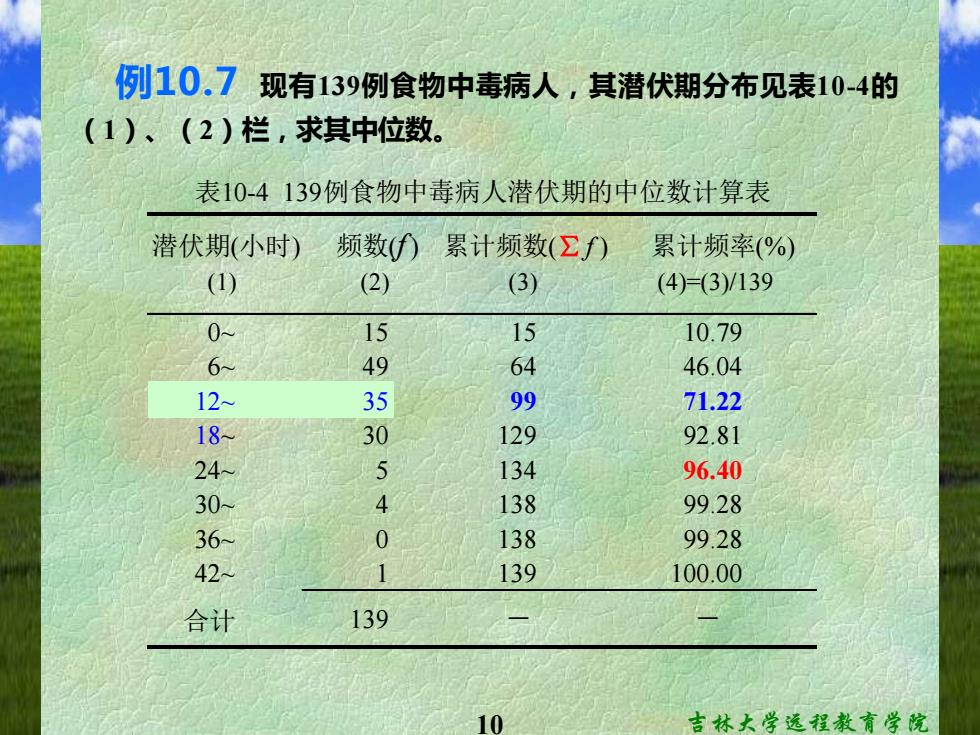
例10.7现有139例食物中毒病人,其潜伏期分布见表10-4的 (1)、(2)栏,求其中位数。 表10-4139例食物中毒病人潜伏期的中位数计算表 潜伏期(小时) 频数()累计频数(Σf) 累计频率(%) () (2) (3) (4)=(3)/139 15 15 10.79 6 49 64 46.04 12~ 35 99 71.22 18 30 129 92.81 24 134 96.40 30 4 138 99.28 36 0 138 99.28 42 139 100.00 合计 139 - 10 吉林大学远程教育学院
10 吉林大学远程教育学院 例10.7 现有139例食物中毒病人,其潜伏期分布见表10-4的 (1)、(2)栏,求其中位数。 潜伏期(小时 ) 频数( f ) 累计频数(∑ f ) 累计频率(%) (1) (2) (3) (4)=(3)/139 0~ 15 15 10.79 6~ 49 64 46.04 12~ 35 99 71.22 18~ 30 129 92.81 24~ 5 134 96.40 30~ 4 138 99.28 36~ 0 138 99.28 42~ 1 139 100.00 合计 139 - - 表10-4 139例食物中毒病人潜伏期的中位数计算表

求出累计频数或累计频率,见表10-4的3)、(4)栏。 本例n/2=139/2=69.5,累计频数99刚好包含n/2,则中位数 落在99所在的第三组段;累计频率71.22%刚好包含50%, 则中位数落在71.22%所在的第三组段。 则L=12,i=6,fM=35,f=64。代入公式 (10.8)得: M=12+639 352 -64)=12.94(小时) 139例食物中毒病人平均潜伏期为12.94小时。 吉林大学远程教育学院
11 吉林大学远程教育学院 求出累计频数或累计频率,见表10-4的(3)、(4)栏。 本例n/2=139/2=69.5,累计频数99刚好包含n/2,则中位数 落在99所在的第三组段;累计频率71.22%刚好包含50%, 则中位数落在71.22%所在的第三组段。 则 L =12,i =6 ,fM =35 ,ΣfL =64。代入公式 (10.8)得: 64) 12.94( ) 2 139 ( 35 6 M =12 + − = 小时 139例食物中毒病人平均潜伏期为12.94小时