
第八节 方差分析 四、多个样本均数的两两比较的g检验 方差分析后,若推断结论是拒绝H。,则意味着 各组样本均数所代表的总体均数间不同或不全相 同。当要了解任意两总体均数间是否存在差别时, 需在方差分析的基础上进一步做多个样本均数的 两两比较,又称为样本均数间的多重比较。 根据所控制误差的类型和大小不同,均数间 差别的多重比较的方法很多。这里介绍常用的q 检验(Student-Newman-Keuls,SNK)。 吉林大学远程教育学院
2 吉林大学远程教育学院 四、多个样本均数的两两比较的q 检验 方差分析后,若推断结论是拒绝H0,则意味着 各组样本均数所代表的总体均数间不同或不全相 同。当要了解任意两总体均数间是否存在差别时, 需在方差分析的基础上进一步做多个样本均数的 两两比较,又称为样本均数间的多重比较。 根据所控制误差的类型和大小不同,均数间 差别的多重比较的方法很多。这里介绍常用的q 检验(Student-Newman-Keuls, SNK)。 第八节 方差分析

q检验的检验统计量的公式为: 9- 公式(10.30) SxA-Xn 公式(10.31 n nB 式中和,是要比较的两样本均数; 5要,-x。 样本均数之差的标准误;n和ns是要比较的两样本含量; MS误差为方差分析中的误差均方。 吉林大学远程教有学院
3 吉林大学远程教育学院 式中 和 是要比较的两样本均数; 为两 样本均数之差的标准误;nA和nB是要比较的两样本含量; MS误差为方差分析中的误差均方。 q 检验的检验统计量的公式为: X A XB A B S X X q − − = ) 1 1 ( 2 A B X X n n MS S A B = + − 误差 公式(10.30) 公式(10.31) X A XB X A XB S −

q的分布与两比较组之间的组间跨度,及自由度v 有关。组间跨度a是指两对比组间所包含的组数( 包括对比组自身);自由度即为保差。 根据组间跨度a,自由度以及检验水准查q界 值表(见教材后附表5),即qa(v,a)。 当求得q≥qa(v,。)时,按a检验水准拒 绝H。,两对比组间差别有统计学意义;反之,尚 不拒绝H0。 下面对例1022资料作均数间的多重比较。 1 吉林大学远程教育学院
4 吉林大学远程教育学院 q 的分布与两比较组之间的组间跨度a 及自由度ν 有关。组间跨度a 是指两对比组间所包含的组数( 包括对比组自身);自由度ν即为ν误差。 根据组间跨度a ,自由度ν以及检验水准α查 q 界 值表(见教材后附表5),即qα(ν,a) 。 当求得 q ≥ qα(ν,a) 时,按α检验水准拒 绝H0,两对比组间差别有统计学意义;反之,尚 不拒绝H0。 下面对例10.22资料作均数间的多重比较

H0:⅓=B H:WWB 0=0.05 将三个样本均数由大到小排列并编组次: 组次 1 2 3 X 1.62 1.20 0.87 组别 甲法 乙法 丙法 本例n1=n2=n3=6,MS误差=0.03078,代入 吉林大学远程教育学院
5 吉林大学远程教育学院 H0 : μA=μB H1 : μA≠μB α= 0.05 将三个样本均数由大到小排列并编组次: Xi 组次 组别 1.62 1.20 0.87 1 2 3 甲法 乙法 丙法 本例n1= n2= n3=6,MS误差=0.03078,代入
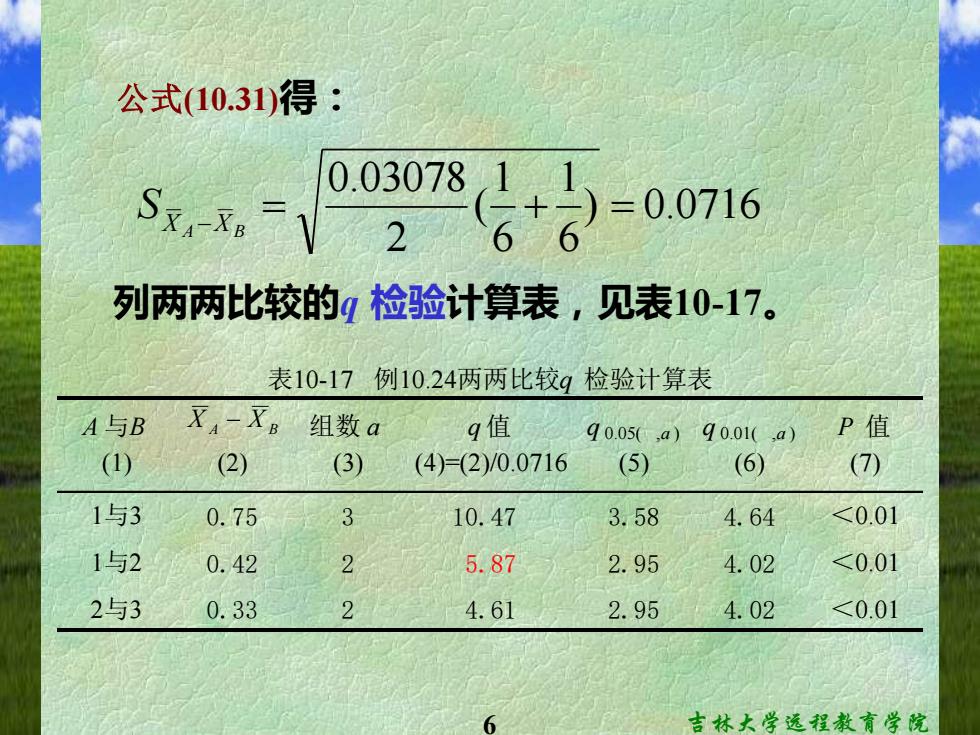
公式(10.31)得: 列两两比较的g检验计算表,见表10-17。 表10-17例10.24两两比较g检验计算表 A与B X4-X。组数a 9值 q0.05,a)90.01(,a) P值 (1) (2) (3) (4)=(2)/0.0716 (5) (6) (7) 1与3 0.75 3 10.47 3.58 4.64 <0.01 1与2 0.42 2 5.87 2.95 4.02 <0.01 2与3 0.33 2 4.61 2.95 4.02 <0.01 吉林大学远程教育学院
6 吉林大学远程教育学院 公式(10.31)得: ) 0.0716 6 1 6 1 ( 2 0.03078 = + = X A −XB S 列两两比较的q 检验计算表,见表10-17。 A 与B 组数 a q 0.05( ,a ) q 0.01( ,a ) P 值 (1) (2) (3) (5) (6) (7) 1与3 0.75 3 10.47 3.58 4.64 <0.01 1与2 0.42 2 5.87 2.95 4.02 <0.01 2与3 0.33 2 4.61 2.95 4.02 <0.01 q 值 (4)=(2)/0.0716 表10-17 例10.24两两比较q 检验计算表 X A − X B

从表10-17中第(7)项可以看出,三组中任两组的 均数处比较差别都有统计学意义。可认为三种不同 的降温方法效果不同,即甲法好,乙法次之,丙法 较差。 需要注意的是:当涉及样本均数处比较的组数大 于2时,若用1检验对各种组合下的两两均数之间进 行检验,则会增大型错误的概率,即可能把本来无 差别的两总体均数判为有差别。因此,多重比较时 不要用检验分别作两两比较。 吉林大学远程教有学院
7 吉林大学远程教育学院 从表10-17中第(7)项可以看出,三组中任两组的 均数比较差别都有统计学意义。可认为三种不同 的降温方法效果不同,即甲法好,乙法次之,丙法 较差。 需要注意的是:当涉及样本均数比较的组数大 于2时,若用t 检验对各种组合下的两两均数之间进 行检验,则会增大I型错误的概率,即可能把本来无 差别的两总体均数判为有差别。因此,多重比较时 不要用t 检验分别作两两比较

第十一章 分类变量的统计分析 第一节分类变量的统计描述 一、分类变量频数表 分类变量的变量值是不连续的,亦称离散变量。 分类变量频数表实际上就是每个变量值的统计个 数(又称绝对数)列表。表111即是一例。 在实际工作中,事物之间的比较不宜用绝对数 需计算相对数。相对数是两个有联系的指标之比。 吉林大学远程散育学院
8 吉林大学远程教育学院 第一节 分类变量的统计描述 一、分类变量频数表 分类变量的变量值是不连续的,亦称离散变量。 分类变量频数表实际上就是每个变量值的统计个 数(又称绝对数)列表。表11-1即是一例。 在实际工作中,事物之间的比较不宜用绝对数, 需计算相对数。相对数是两个有联系的指标之比。 第十一章 分类变量的统计分析

二、常用相对数 常用相对数有:率、构成比和相对比。 ()率 率(rate)又称频率指标。说明某现象发生的 频度或强度。常以百分率(%)、干分率(%)、万 分率(1万)、十万分率(1/10万)等表示。计算公式 为: 率 某现象实际的发生数 ×100%(或1000%o..) 可能发生该现象的总数 吉林大学远程教育学院
9 吉林大学远程教育学院 常用相对数有:率、构成比和相对比。 二、常用相对数 ㈠ 率 率(rate)又称频率指标。说明某现象发生的 频度或强度。常以百分率(%)、千分率(‰)、万 分率(1/万)、十万分率(1/10万)等表示。计算公式 为: (或 ) 可能发生该现象的总数 某现象实际的发生数 率 = 100% 1000‰

表111中患病率的大小体现了不同地区脊柱侧凸 患病强度的大小。 白构成比 构成比(proportion)又称构成指标。说明某事 物内部某组成部分占其全部的比重或分布。计 算公式为: 构成比= 某一组成部分的例数 ×100% 同二事物所有组成部分的总例数 表111中阳性数构成比的大小体现了不同地区 10 吉林大学远程教育学院
10 吉林大学远程教育学院 表11-1中患病率的大小体现了不同地区脊柱侧凸 患病强度的大小。 ㈡ 构成比 构成比(proportion)又称构成指标。说明某事 物内部某组成部分占其全部的比重或分布。计 算公式为: = 100% 同一事物所有组成部分的总例数 某一组成部分的例数 构成比 表11-1中阳性数构成比的大小体现了不同地区

脊柱侧凸患病的例数在总例数中所占的比重大小。 (白)相对比 相对比(relative ratio)亦称比(ratio),又称对 比指标。说明两个有关指标比对的水平,常用倍数 或百分数表示。计算公式为: 相对比= 甲指标 或×100%) 乙指标 两个对比指标可以是绝对数、相对数或平均数等 。如某地的男女性别比即为绝对数之比;两地区 吉林大学远程教育学院
11 吉林大学远程教育学院 脊柱侧凸患病的例数在总例数中所占的比重大小。 ㈢ 相对比 相对比(relative ratio)亦称比(ratio),又称对 比指标。说明两个有关指标比对的水平,常用倍数 或百分数表示。计算公式为: (或 ) 乙指标 甲指标 相对比 = 100% 两个对比指标可以是绝对数、相对数或平均数等 。如某地的男女性别比即为绝对数之比;两地区