
第四节 正态分布和医学参考值范围 、 正态分布 在实际应用中,对于某些频数分布表资料绘 制成的直方图(如本章第一节的例101的图101) 如果不断地加大样本并细分组段,则图中的直条 将逐渐变窄并且锯齿型上缘就会趋近某一光滑的 曲线(称为频数曲线或频率曲线),该曲线的形 态为开口向下的钟型,两头低,中间高,左右对 称,它近似于正态分布曲线。见下图10-2。 吉林大学远程教育学院
2 吉林大学远程教育学院 第四节 正态分布和医学参考值范围 一、正态分布 在实际应用中,对于某些频数分布表资料绘 制成的直方图(如本章第一节的例10.1的图10-1), 如果不断地加大样本并细分组段,则图中的直条 将逐渐变窄并且锯齿型上缘就会趋近某一光滑的 曲线(称为频数曲线或频率曲线),该曲线的形 态为开口向下的钟型,两头低,中间高,左右对 称,它近似于正态分布曲线。见下图10-2
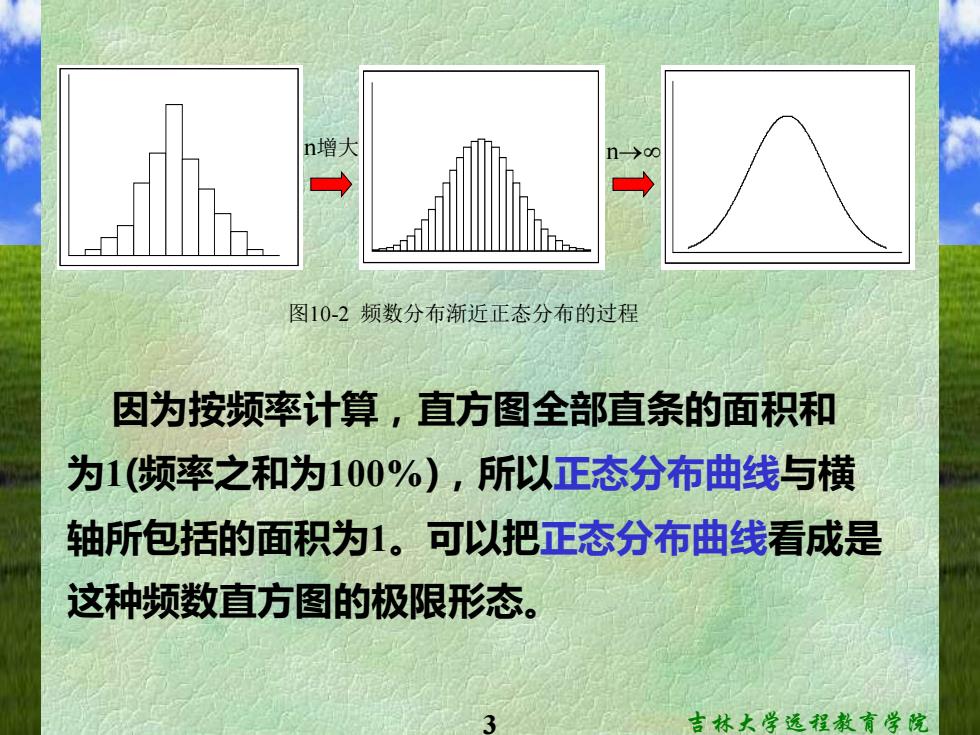
n增 图10-2频数分布渐近正态分布的过程 因为按频率计算,直方图全部直条的面积和 为1(频率之和为100%),所以正态分布曲线与横 轴所包括的面积为1。可以把正态分布曲线看成是 这种频数直方图的极限形态。 吉林大学远程教育学院
3 吉林大学远程教育学院 因为按频率计算,直方图全部直条的面积和 为1(频率之和为100%),所以正态分布曲线与横 轴所包括的面积为1。可以把正态分布曲线看成是 这种频数直方图的极限形态。 图10-2 频数分布渐近正态分布的过程 n增大 n→

(合)正态分布的概念和图形 正态分布(Normal distribution)又被称为高斯 分布(Gaussian distribution),是一种重要的连续 分布。其分布密度函数为: (x-)2 1 f(x)= e 202 G√2元 00<x<十00 式中是总体均数,O是总体标准差,π=3.14159。 为圆周率,e=2.71828是自然对数的底。 吉林大学远程教育学院
4 吉林大学远程教育学院 正态分布(Normal distribution)又被称为高斯 分布(Gaussian distribution),是一种重要的连续 分布。其分布密度函数为: ㈠ 正态分布的概念和图形 2 2 2 ( ) 2 1 ( ) − − = x f x e − x + 式中μ是总体均数,σ是总体标准差,π=3.14159... 为圆周率,e=2.71828...是自然对数的底
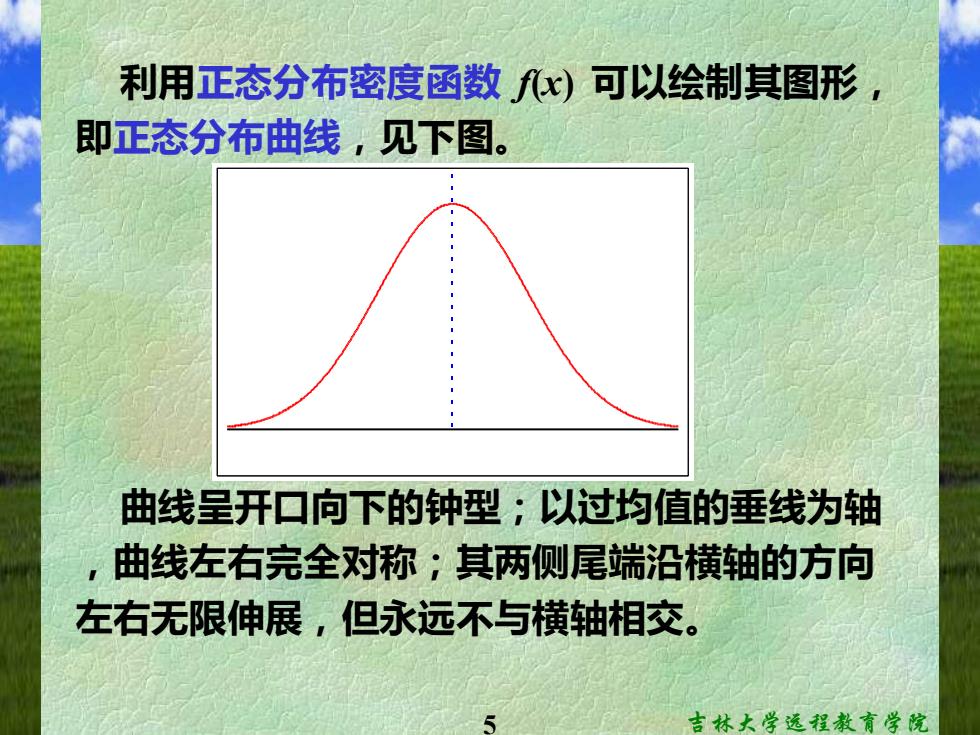
利用正态分布密度函数x)可以绘制其图形 即正态分布曲线,见下图。 曲线呈开口向下的钟型;以过均值的垂线为轴 ,曲线左右完全对称;其两侧尾端沿横轴的方向 左右无限伸展,但永远不与横轴相交。 吉林大学远程教育学院
5 吉林大学远程教育学院 利用正态分布密度函数 f(x) 可以绘制其图形, 即正态分布曲线,见下图。 曲线呈开口向下的钟型;以过均值的垂线为轴 ,曲线左右完全对称;其两侧尾端沿横轴的方向 左右无限伸展,但永远不与横轴相交

(白)正态分布的特征 ①正态曲线以均数为中心,左右对称。 ②正态曲线的高峰位于均数所在处。 ③正态分布具有均值与标准差两个参数。 确定正态曲线的中心位置。越大,曲 线沿横轴越向右移动;反之越向左移动。σ 确定曲线的形状。o越大,曲线越扁平;σ 越小,曲线越尖峭。一般用N(山,c2)表示 均数为μ,方差为G的正态分布。 ④正态曲线下面积分布有一定规律。 吉林大学远程教育学院
6 吉林大学远程教育学院 ㈡ 正态分布的特征 ① 正态曲线以均数为中心,左右对称。 ② 正态曲线的高峰位于均数所在处。 ③ 正态分布具有μ均值与σ标准差两个参数。 μ确定正态曲线的中心位置。μ越大,曲 线沿横轴越向右移动;反之越向左移动。σ 确定曲线的形状。σ越大,曲线越扁平;σ 越小,曲线越尖峭。一般用N(μ,σ 2 )表示 均数为μ,方差为σ2的正态分布。 ④ 正态曲线下面积分布有一定规律
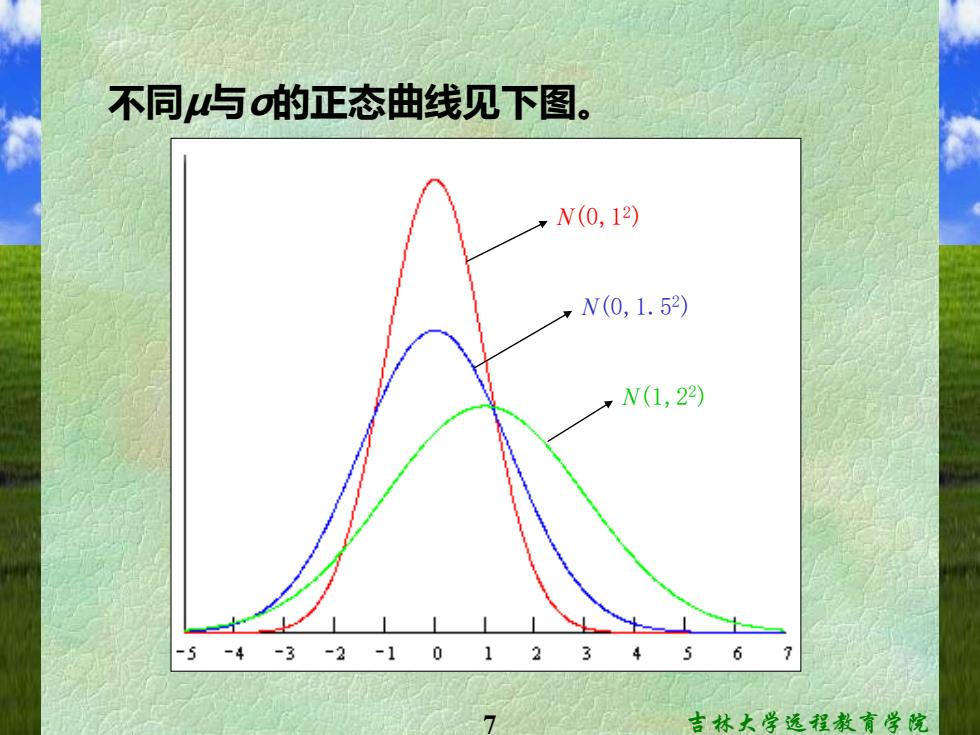
不同μ与的正态曲线见下图。 ,N(0,12) N(0,1.52) N(1,22) -5 -4-3-2-101234567 吉林大学远程教育学院
7 吉林大学远程教育学院 不同μ与σ的正态曲线见下图。 N(0,12) N(0,1.52) N(1,22)

二、正态曲线下面积分布规律 实际应用中,正态曲线下,横轴上一定区间 的面积占总面积的百分数,可以估计该区间的例 数占总例数的百分数或变量值落在该区间的概率。 利用对正态分布密度函数x)求积分可以得 到正态曲线下一定区间的面积(概率),即: F(x)=[f(x)dx 式中F(x)称为正态变量x的累计分布函数 8 吉林大学远程教育学院
8 吉林大学远程教育学院 二、正态曲线下面积分布规律 实际应用中,正态曲线下,横轴上一定区间 的面积占总面积的百分数,可以估计该区间的例 数占总例数的百分数或变量值落在该区间的概率。 利用对正态分布密度函数f(x)求积分可以得 到正态曲线下一定区间的面积(概率),即: − = x F(x) f (x)dx 式中F(x)称为正态变量x的累计分布函数
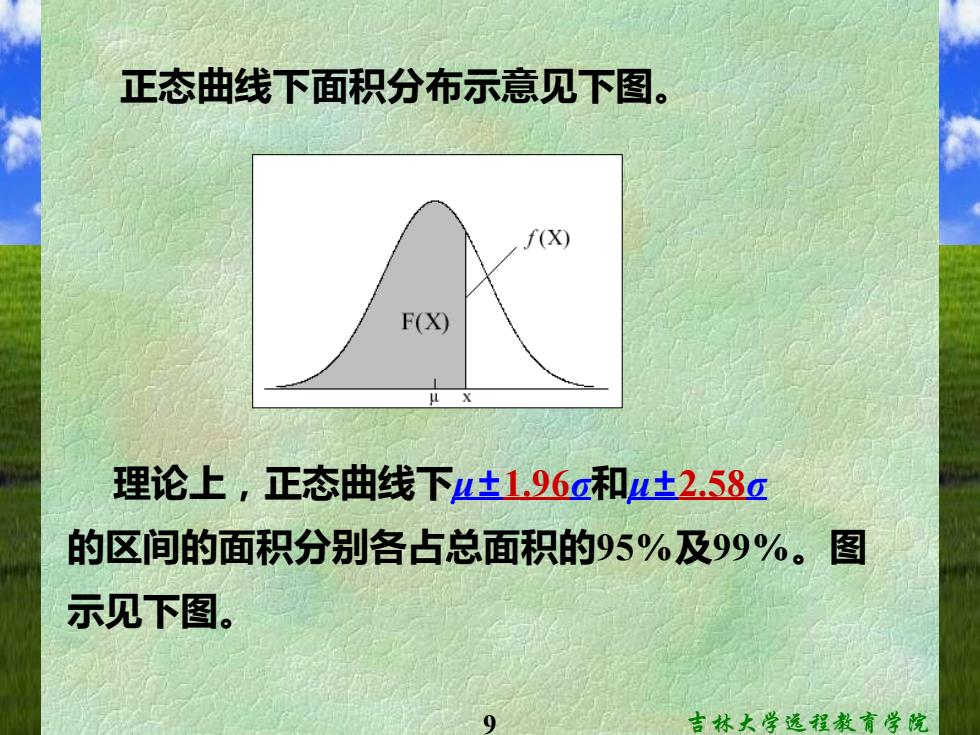
正态曲线下面积分布示意见下图。 f(X) F(X) 理论上,正态曲线下±196和±2.58a 的区间的面积分别各占总面积的95%及99%。图 示见下图。 9 吉林大学远程教育学院
9 吉林大学远程教育学院 正态曲线下面积分布示意见下图。 理论上,正态曲线下μ±1.96σ和μ±2.58σ 的区间的面积分别各占总面积的95%及99%。图 示见下图

950% 99% 2.5% 2.5% 0.5% 0.5% -2.58c 4+2.58a 4-1.960 4 +1.96a 三、标准正态分布 正态分布有两个不固定的参数与σ,为了应用 方便,可采取变量变换,使二者都为常数,即咋 0,01。其变换为: 10 吉林大学远程教育学院
10 吉林大学远程教育学院 三、标准正态分布 正态分布有两个不固定的参数μ与σ,为了应用 方便,可采取变量变换,使二者都为常数,即μ= 0,σ= 1。其变换为:
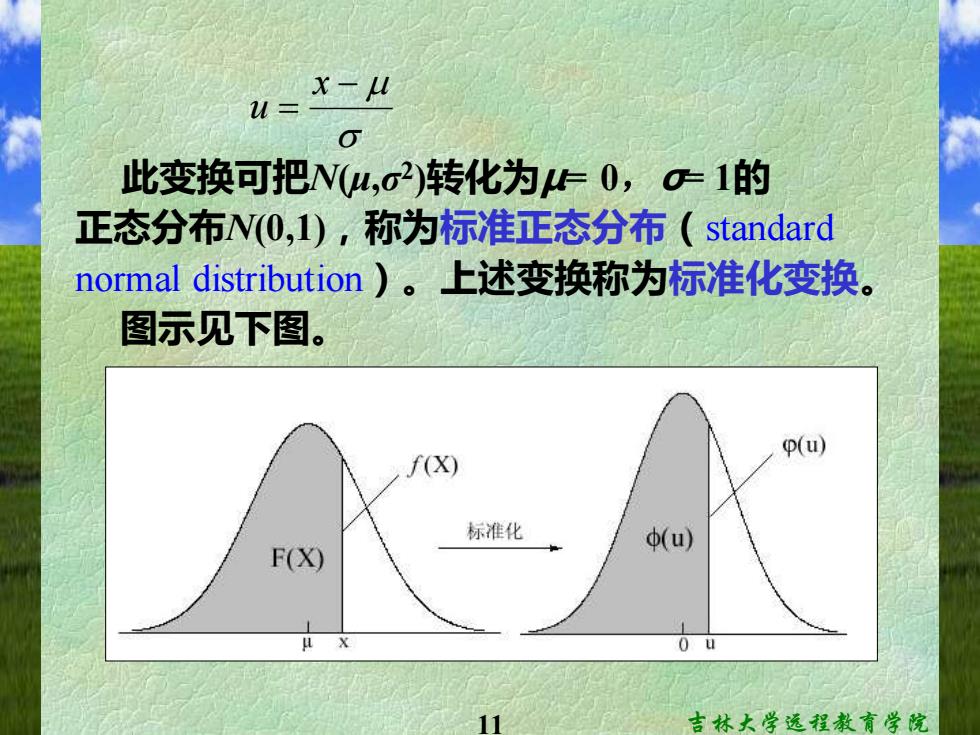
U=X-H 此变换可把N(4,c2)转化为E0,σ正1的 正态分布N(0,1),称为标准正态分布(standard normal distribution)。上述变换称为标准化变换。 图示见下图。 (u) f(X) 标准化 F(X) (u) 0日 11 吉林大学远程教育学院
11 吉林大学远程教育学院 − = x u 此变换可把N(μ,σ 2 )转化为μ= 0,σ= 1的 正态分布N(0,1),称为标准正态分布(standard normal distribution)。上述变换称为标准化变换。 图示见下图