
第八节方差分析 一、方差分析的基本思想 前一节所讲的t检验和u检验只适用于一组或 两组样本均数的比较,对于两组以上样本均数的 比较需要采用方差分析(analysis of variance,简记 ANOVA)。 方差分析的基本思想可通过下述例题10.22 说明。 吉林大学远程教育学院
2 吉林大学远程教育学院 第八节 方差分析 一、方差分析的基本思想 前一节所讲的t 检验和u 检验只适用于一组或 两组样本均数的比较,对于两组以上样本均数的 比较需要采用方差分析(analysis of variance, 简记 ANOVA)。 方差分析的基本思想可通过下述例题10.22 说明
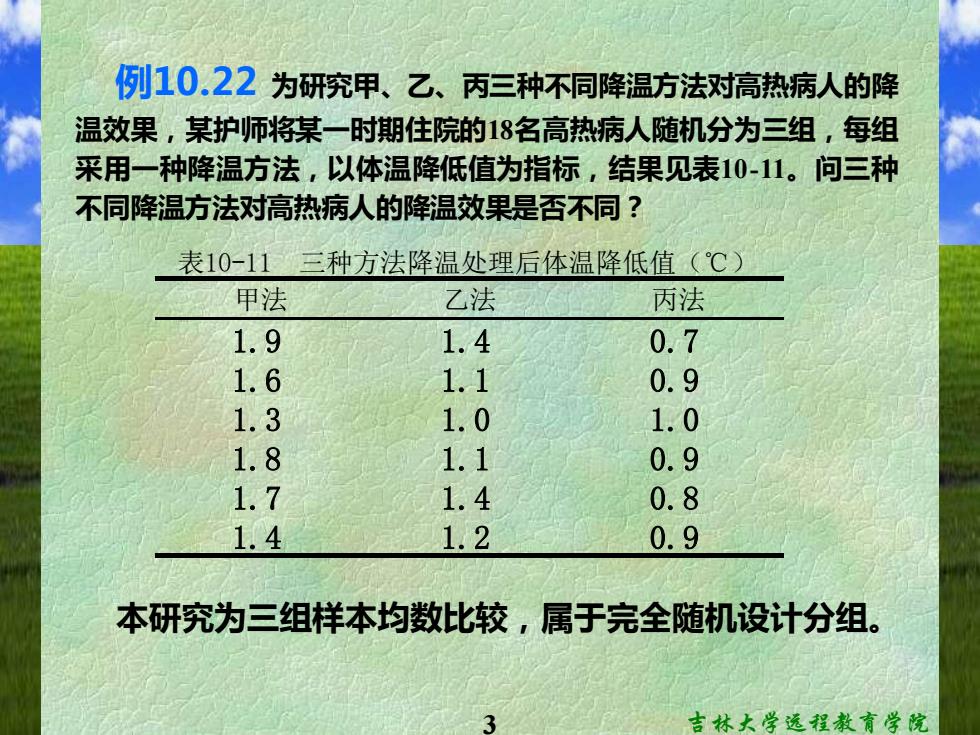
例10,22为研究甲、乙、丙三种不同降温方法对高热病人的降 温效果,某护师将煤一时期住院的18名高热病人随机分为三组,每组 采用一种降温方法,以体温降低值为指标,结果见表10-11。问三种 不同降温方法对高热病人的降温效果是否不同? 表10-11 三种方法降温处理后体温降低值(℃) 甲法 乙法 丙法 1.9 1.4 0.7 1.6 1.1 0.9 1.3 1.0 1.0 1.8 1.1 0.9 1.7 1.4 0.8 1.4 1.2 0.9 本研究为三组样本均数处比较,属于完全随机设计分组。 吉林大学远程教育学院
3 吉林大学远程教育学院 例10.22 为研究甲、乙、丙三种不同降温方法对高热病人的降 温效果,某护师将某一时期住院的18名高热病人随机分为三组,每组 采用一种降温方法,以体温降低值为指标,结果见表10-11。问三种 不同降温方法对高热病人的降温效果是否不同? 本研究为三组样本均数比较,属于完全随机设计分组。 甲法 乙法 丙法 1.9 1.4 0.7 1.6 1.1 0.9 1.3 1.0 1.0 1.8 1.1 0.9 1.7 1.4 0.8 1.4 1.2 0.9 表10-11 三种方法降温处理后体温降低值(℃)

从测定结果看,全部18例数据的不同可形成 三种变异: 1.总变异全部测定值的大小不同体现了总变 异,其测度可用所有的测定值X,与总均数的离均 差平方和表示,记为SS总: SSa=∑∑(X,-)3 i=1= 式中用X表示第i个组的第个测定值,i=1,2,,k, 广=1,2,.,1。全部测定值的总均数用轰示。 吉林大学远程教育学院
4 吉林大学远程教育学院 从测定结果看,全部18例数据的不同可形成 三种变异: 1. 总变异 全部测定值的大小不同体现了总变 异,其测度可用所有的测定值Xij与总均数 的离均 差平方和表示,记为SS总: X = = = − k i n j i j i SS X X 1 1 2 总 ( ) 式中用Xij 表示第i 个组的第j 个测定值,i =1,2,…,k , j =1,2,…,ni 。全部测定值的总均数用 X 表示

由于离均差平方和受到观测值的个数多少的影响 ,故SS总也与总例数N有关,确切地是与总的自由 度隐有关: 总=N-1 2.组间变异各组的样本均数的不同体现了组 间变异,它常反映的是处理因素或研究因素的效 应,也包括了随机误差的影响。其测度可用各组 的样本均数与总均数的离均差平方和表示: 吉林大学远程教育学院
5 吉林大学远程教育学院 2. 组间变异 各组的样本均数 的不同体现了组 间变异,它常反映的是处理因素或研究因素的效 应,也包括了随机误差的影响。其测度可用各组 的样本均数 与总均数 的离均差平方和表示: 由于离均差平方和受到观测值的个数多少的影响 ,故SS总也与总例数N有关,确切地是与总的自由 度ν总有关: ν总= N-1 Xi Xi X
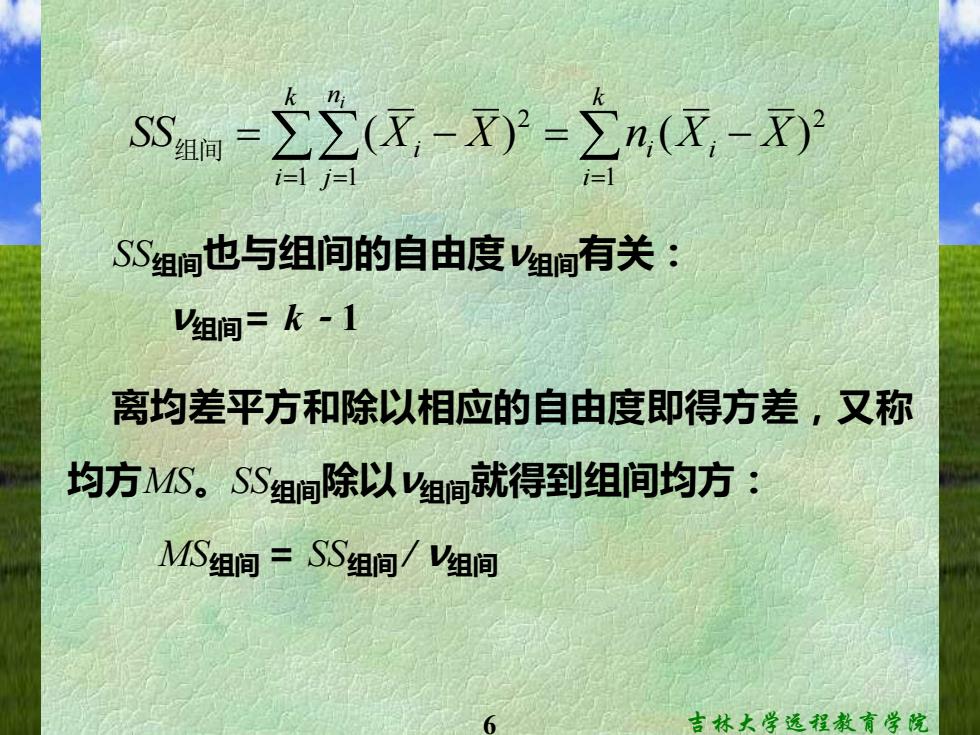
SSm=(X)=2n(X-X) i=l ia SS组间也与组间的自由度V组间有关: V组间=k-1 离均差平方和除以相应的自由度即得方差,又称 均方MS。SS组间除以V组间就得到组间均方: MS组间=SS组间/V组间 吉林大学远程教育学院
6 吉林大学远程教育学院 SS组间也与组间的自由度ν组间有关: ν组间= k-1 = = = = − = − k i i i k i n j SS Xi X n X X i 1 2 1 1 2 组间 ( ) ( ) 离均差平方和除以相应的自由度即得方差,又称 均方MS。SS组间除以ν组间就得到组间均方: MS组间 = SS组间 / ν组间

3.组内变异各组内的观测值的不同体现了组内 变异,它主要反映的是由个体差异、测量误差、 偶然因素等等造成的随机误差的影响。其测度可 用各组的每个观测值X,与本组均数的离趵差平方 和表示: SS4=2(X,X,) i=1j= SS组内的自由度V组内为: 组内=N-K 吉林大学远程教育学院
7 吉林大学远程教育学院 3. 组内变异 各组内的观测值的不同体现了组内 变异,它主要反映的是由个体差异、测量误差、 偶然因素等等造成的随机误差的影响。其测度可 用各组的每个观测值Xij与本组均数 的离均差平方 和表示: Xi = = = − k i n j i j i i SS X X 1 1 2 组内 ( ) SS组内的自由度ν组内为: ν组内= N- k

SS组内除以组内就得到组内均方: MS组内=SS组内/组内 对于完全随机设计分组的多个样本均数的比 较,上述三种变异有以下关系: SS总=SS组间+SS组内 V总=V组间+组内 本例若三组样本均数来自同一总体,即: H0:μ甲=乙=丙 吉林大学远程教育学院
8 吉林大学远程教育学院 SS组内除以ν组内就得到组内均方: MS组内 = SS组内 / ν组内 对于完全随机设计分组的多个样本均数的比 较,上述三种变异有以下关系: SS总 = SS组间+ SS组内 ν总 = ν组间+ ν组内 本例若三组样本均数来自同一总体,即: H0 : μ甲=μ乙=μ丙

则意味着三种不同降温方法效果总体相同,即组 问变异与组内变异均只反映随机误差,若计算组间 均方与组内均方的比值(即F值): F=MS组间/MS组内 F值应接近1。反之,若三种不同降温方法效果 总体不相同,则组间变异中多了处理因素(降 温方法)的效应,组间变异大于组内变异,上述 F值明显大于1。那么大到多大程度才有统计学意义 ?根据统计学家推导出上述统计量F的分布,通 吉林大学远程教育学院
9 吉林大学远程教育学院 则意味着三种不同降温方法效果总体相同,即组 间变异与组内变异均只反映随机误差,若计算组间 均方与组内均方的比值(即F值): F = MS组间/ MS组内 F值应接近1。反之,若三种不同降温方法效果 总体不相同,则组间变异中多了处理因素(降 温方法)的效应,组间变异大于组内变异,上述 F值明显大于1。那么大到多大程度才有统计学意义 ?根据统计学家推导出上述统计量F的分布,通

过查F界值表,得到在a检验水准下H成立与否的 概率P,从而作出推断结论。 方差分析的应用条件: ①各样本相互独立; ②各样本来自正态分布总体; ③各样本总体方差相等(方差齐)。 F界值常用F表秀,其中a为检验水准; V为分子自由度,即组间自由度V组间;V2为分 母自由度,即组内自由度V组内。可从教材后的 10 吉林大学远程教育学院
10 吉林大学远程教育学院 过查F界值表,得到在α检验水准下H0成立与否的 概率P ,从而作出推断结论。 方差分析的应用条件: ① 各样本相互独立; ② 各样本来自正态分布总体; ③ 各样本总体方差相等(方差齐)。 F界值常用 表示,其中α为检验水准; ν1为分子自由度,即组间自由度ν组间;ν2为分 母自由度,即组内自由度ν组内。可从教材后的 ( , ) 1 2 F
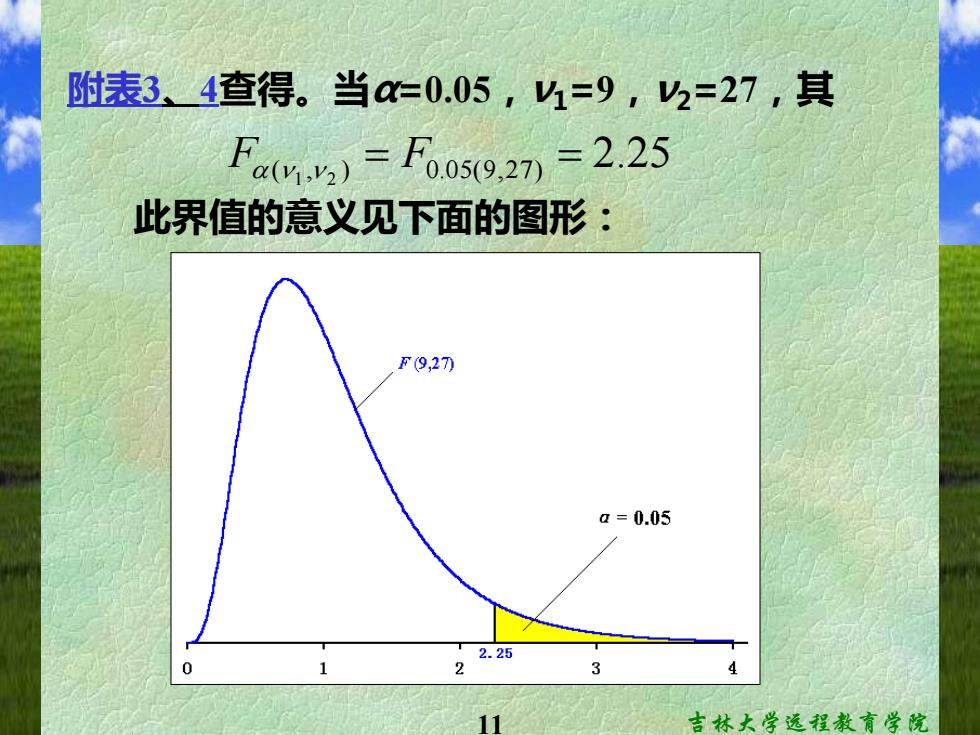
附表3、4查得。当a=0.05,=9,2=27,其 F4)=f005927)=2.25 此界值的意义见下面的图形: F9,27) a=0.05 2.25 0 2 3 吉林大学远程教育学院
11 吉林大学远程教育学院 附表3、4查得。当α=0.05,ν1=9,ν2=27,其 此界值的意义见下面的图形: ( , ) 0.0 5(9,2 7) 2.25 1 2 F = F =