
第五节均数的抽样误差和总体均数的估计 一、均数的抽样误差和标准误 (口)均数的抽样误差 由于总体常常不能直接研究,因此从总体中 随机抽取一定数量的观测值作为样本进行抽样研 究(sampling study)成为统计研究的最基本的方 法。变异的存在使得样本指标与总体指标不一定 恰恰相等。这种由抽样造成的统计量与总体参数 的差异叫抽样误差。抽样误差是不可避免的。 吉林大学远程教育学院
2 吉林大学远程教育学院 第五节 均数的抽样误差和总体均数的估计 一、均数的抽样误差和标准误 由于总体常常不能直接研究,因此从总体中 随机抽取一定数量的观测值作为样本进行抽样研 究(sampling study)成为统计研究的最基本的方 法。变异的存在使得样本指标与总体指标不一定 恰恰相等。这种由抽样造成的统计量与总体参数 的差异叫抽样误差。抽样误差是不可避免的。 ㈠ 均数的抽样误差

(仁)标准误 研究抽样误差的大小的变化规律对于由样本指 标推断总体指标非常有意义。 统计学基础理论的中心极限定理指出: ①从正态分布总体N(u,σ)中随机抽取容量 为n的样本,其样本均数限从正态分布 N(山o谋中可按式计算: 0双 公式(10.19) n ②如果一个变量的总体分布具有均数和标 准差o,则从该总体抽得的容量为n的样本, 吉林大学远程教育学院
3 吉林大学远程教育学院 ① 从正态分布总体N(μ,σ 2 )中随机抽取容量 为n的样本,其样本均数 服从正态分布 。其中 可按下式计算: 研究抽样误差的大小的变化规律对于由样本指 标推断总体指标非常有意义。 统计学基础理论的中心极限定理指出: X ( , ) 2 N X X n X = ② 如果一个变量的总体分布具有均数μ和标 准差σ,则从该总体抽得的容量为n的样本, 公式(10.19) ㈡ 标准误

在趋于无穷大时,样本均数的分布趋向正态分 布 N(ui,o) 定理的直观表述见下图。 x总体 X总体 X1 X4 样本1 X2 2 样本2 n 2 X3 Xi-1 样本 n x~N(4,o2) X-NuG) n 吉林大学远程教育学院
4 吉林大学远程教育学院 在n趋于无穷大时,样本均数 的分布趋向正态分 布 。 X ( , ) 2 N X 定理的直观表述见下图。 ~ ( , ) 2 x N x总体 X1 x2 x3 x1 xi-2 xi-1 x4 xi . . . 样本1 n 样本2 样本j ... ... ... X2 X j ... ... X 总体 ~ ( , ) 2 n X N n n

为了理解中心极限定理,特用一个模拟实验 例子来说明。 例某地假定1979年成都市16岁女学生的身高服从均数为155.4 cm、标准差为5.3cm的正态分布。用电子计算机做抽样模拟实验,从 N(155.4,5.32)的总体中,每次随机抽出10个数字(即样本含量n=10), 组成一个样本,求出样本均数及标准差S。 例如1号样本的10数字为: 154.4151.6159.2145.5152.2150.6158.6151.9157.1 由此求得X1与1S25。 仿此方式抽取100次,每次均抽出10个数字,可求得100个样 本均数及标准差,具体见表1。 通过计算这100个样本均数的均数和标准差 来了解均数的抽样误差的变化规律。 吉林大学远程教育学院
5 吉林大学远程教育学院 为了理解中心极限定理,特用一个模拟实验 例子来说明。 例 某地假定1979年成都市16岁女学生的身高服从均数为155.4 cm、标准差为5.3cm的正态分布。用电子计算机做抽样模拟实验,从 N(155.4,5.3 2 )的总体中,每次随机抽出10个数字(即样本含量n=10), 组成一个样本,求出样本均数 及标准差S。 例如1号样本的10数字为: 154.4 151.6 159.2 145.5 152.2 150.6 158.6 151.9 157.1 由此求得 ,S1=4.15。 仿此方式抽取100次,每次均抽出10个数字,可求得100个样 本均数及标准差,具体见表1。 X X1 =153.62 通过计算这100个样本均数的均数和标准差, 来了解均数的抽样误差的变化规律
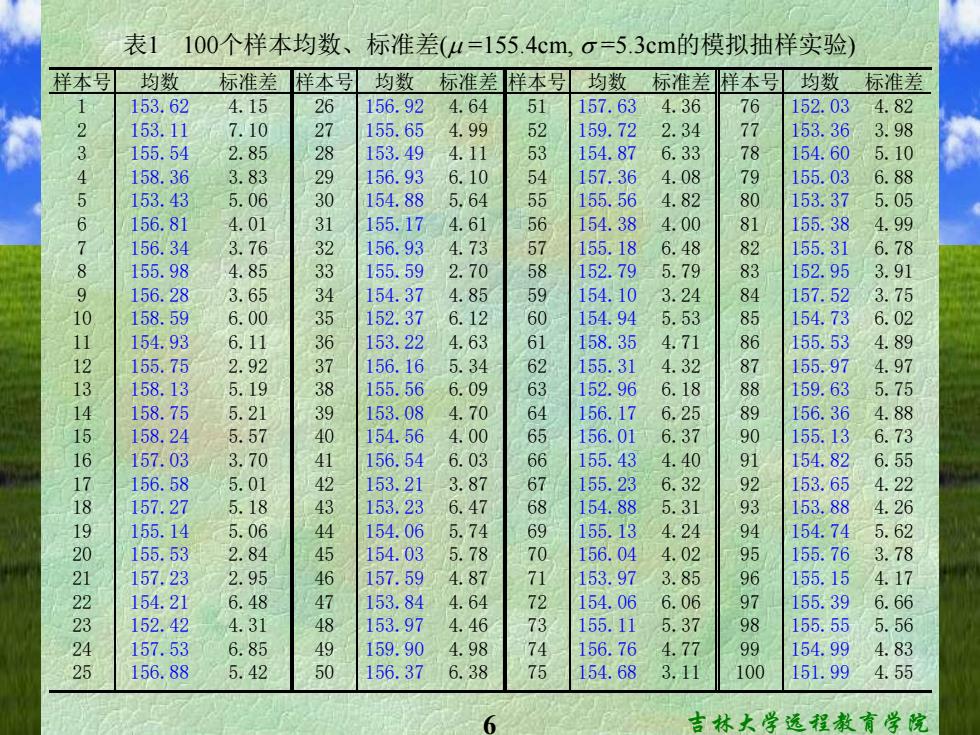
表1100个样本均数、 标准差(4=155.4cm,σ=5.3cm的模拟抽样实验) 样本号 均数 标准差 样本号 均数标准差样本号 均数 标准差样本号均数 标准差 1 153.62 4.15 26 156.924.64 51 157.63 4.36 76 152.03 4.82 2 153.11 7.10 7 155.654.99 2 159.72 2.34 7 153.36 3.98 3 155.54 2.85 28 153.494.11 53 154.87 6.33 7 154.605.10 4 158.36 3.83 9 156.93 6.10 54 157.36 4.08 79 155.03 6.88 5 153.43 5.06 30 154.88 5.64 55 155.56 4.82 0 153.37 5.05 6 156.81 4.01 31 155.17 4.61 154.38 4.00 8 155.38 4.99 1 156.34 3.76 32 156.93 4.73 1 155.18 6.48 155.316.78 155.98 4.85 3 155.59 2.70 152.79 5.79 3 152.95 3.91 9 156.28 3.65 154.37 4.85 154.10 3.24 157.52 3.75 158.59 6.00 3 152.376.12 154.94 5.53 8 154.73 6.02 11 154.93 6.11 6 153.22 4.63 61 158.35 4.71 155.53 4.89 12 155.75 2.92 37 156.16 5.34 155.31 4.32 87 155.97 4.97 13 158.13 5.19 3 155.56 6.09 酷 152.96 6.18 159.63 5.75 158.75 5.21 39 153.08 4.70 6 156.17 6.25 8 156.36 4.88 15 158.24 5.57 0 154.56 4.00 156.01 6.37 155.13 6.73 16 157.03 3.70 41 156.54 6.03 155.43 4.40 154.82 6.55 17 156.58 5.01 42 153.21 3.87 67 155.23 6.32 153.65 4.22 18 157.27 5.18 43 153.23 6.47 6 154.88 5.31 93 153.88 4.26 19 155.14 5.06 44 154.06 5.74 155.13 4.24 154.74 5.62 20 155.53 2.84 45 154.03 5.78 70 156.04 4.02 95 155.76 3.78 157.23 2.95 46 157.59 4.87 153.97 3.85 6 155.15 4.17 22 154.21 6.48 153.84 4.64 72 154.06 6.06 9 155.396.66 152.42 4.31 8 153.97 4.46 34 155.11 5.37 8 155.55 5.56 4 157.53 6.85 49 159.90 4.98 156.76 4.77 99 154.99 4.83 25 156.88 5.42 50 156.37 6.38 75 154.68 3.11 100 151.99 4.55 吉林大学远程教育学院
6 吉林大学远程教育学院 样本号 均数 标准差 样本号 均数 标准差 样本号 均数 标准差 样本号 均数 标准差 1 153.62 4.15 26 156.92 4.64 51 157.63 4.36 76 152.03 4.82 2 153.11 7.10 27 155.65 4.99 52 159.72 2.34 77 153.36 3.98 3 155.54 2.85 28 153.49 4.11 53 154.87 6.33 78 154.60 5.10 4 158.36 3.83 29 156.93 6.10 54 157.36 4.08 79 155.03 6.88 5 153.43 5.06 30 154.88 5.64 55 155.56 4.82 80 153.37 5.05 6 156.81 4.01 31 155.17 4.61 56 154.38 4.00 81 155.38 4.99 7 156.34 3.76 32 156.93 4.73 57 155.18 6.48 82 155.31 6.78 8 155.98 4.85 33 155.59 2.70 58 152.79 5.79 83 152.95 3.91 9 156.28 3.65 34 154.37 4.85 59 154.10 3.24 84 157.52 3.75 10 158.59 6.00 35 152.37 6.12 60 154.94 5.53 85 154.73 6.02 11 154.93 6.11 36 153.22 4.63 61 158.35 4.71 86 155.53 4.89 12 155.75 2.92 37 156.16 5.34 62 155.31 4.32 87 155.97 4.97 13 158.13 5.19 38 155.56 6.09 63 152.96 6.18 88 159.63 5.75 14 158.75 5.21 39 153.08 4.70 64 156.17 6.25 89 156.36 4.88 15 158.24 5.57 40 154.56 4.00 65 156.01 6.37 90 155.13 6.73 16 157.03 3.70 41 156.54 6.03 66 155.43 4.40 91 154.82 6.55 17 156.58 5.01 42 153.21 3.87 67 155.23 6.32 92 153.65 4.22 18 157.27 5.18 43 153.23 6.47 68 154.88 5.31 93 153.88 4.26 19 155.14 5.06 44 154.06 5.74 69 155.13 4.24 94 154.74 5.62 20 155.53 2.84 45 154.03 5.78 70 156.04 4.02 95 155.76 3.78 21 157.23 2.95 46 157.59 4.87 71 153.97 3.85 96 155.15 4.17 22 154.21 6.48 47 153.84 4.64 72 154.06 6.06 97 155.39 6.66 23 152.42 4.31 48 153.97 4.46 73 155.11 5.37 98 155.55 5.56 24 157.53 6.85 49 159.90 4.98 74 156.76 4.77 99 154.99 4.83 25 156.88 5.42 50 156.37 6.38 75 154.68 3.11 100 151.99 4.55 表1 100个样本均数、标准差( =155.4cm, =5.3cm的模拟抽样实验)

求得此100个样本均数的均数及样本均数的标准差(称标 准误)为 : 无 Xx=白 X1+X2++X100_15362+153.11++151.99 100 100 100 =155.38(cm) Za ro 153.62-155.382+153.11-155.382+.+151.99-155.38)2 Sx= =1.71(cm) 100 100 由中心极限定理可知:①样本均数的总体均 数等于μ。本实验求得此100个样本均数的均数为 155.38,而u=155.4,二者非常相近。②标准误 按公式10,1计算,·=50本实验求得 的标准误为1.71,二者也很相近。 吉林大学远程教育学院
7 吉林大学远程教育学院 求得此100个样本均数的均数及样本均数的标准差(称标 准误)为: 155.38( ) 100 153.62 153.11 ... 151.99 100 ... 100 1 2 100 100 1 cm X X X X X i i X = + + + = + + + = = = 1.71( ) 100 (153.62 155.38) (153.11 155.38) ... (151.99 155.38) 100 ( ) 2 2 2 100 1 2 cm X X S i i X X = − + − + + − = − = = 由中心极限定理可知:①样本均数的总体均 数等于μ。本实验求得此100个样本均数的均数为 155.38,而μ= 155.4,二者非常相近。②标准误 按公式(10.19)计算, 。本实验求得 的标准误为1.71,二者也很相近。1.68 10 = 5.3 = X

如果增大抽样次数,求得的均数与标准误将更 加接近理论值。 再把上述实验求得的100个样本均数编制成频 数表(见表2),并绘制成直方图(见图1),可以看 到此频数分布近似正态分布;如果增大抽样次数, 频数分布将更加逼近正态分布。 当抽样次数趋近无穷大时,此抽样(即样本 含量=10)所得到的样本均数的分布服从总体均 数也为,总体标准误为O的正态分布 n (即N155.4,682) 吉林大学远程教有学院
8 吉林大学远程教育学院 如果增大抽样次数,求得的均数与标准误将更 加接近理论值。 再把上述实验求得的100个样本均数编制成频 数表(见表2),并绘制成直方图(见图1),可以看 到此频数分布近似正态分布;如果增大抽样次数, 频数分布将更加逼近正态分布。 当抽样次数趋近无穷大时,此抽样(即样本 含量n=10)所得到的样本均数的分布服从总体均 数也为μ,总体标准误为 的正态分布 (即 )。 n (155.4,1.68 ) 2 N

30 表2100个样本均数的频数表 均数组段(cm) 频数 25 151 1 20 152- 6 153 15 盞15 154 19 155 27 10 156 16 157 8 158 6 159 3 0 151152153154155156157158159 合计 100 身高均数(cm) 图1100个样本均数的直方图 下面的流程图将演示此模拟实验的全过程。 0 吉林大学远程教育学院
9 吉林大学远程教育学院 均数组段(cm) 频数 151~ 1 152~ 6 153~ 15 154~ 19 155~ 27 156~ 16 157~ 8 158~ 5 159~ 3 合计 100 0 5 10 15 20 25 30 151~ 152~ 153~ 154~ 155~ 156~ 157~ 158~ 159~ 身高均数(cm) 频数 表2 100个样本均数的频数表 图1 100个样本均数的直方图 下面的流程图将演示此模拟实验的全过程
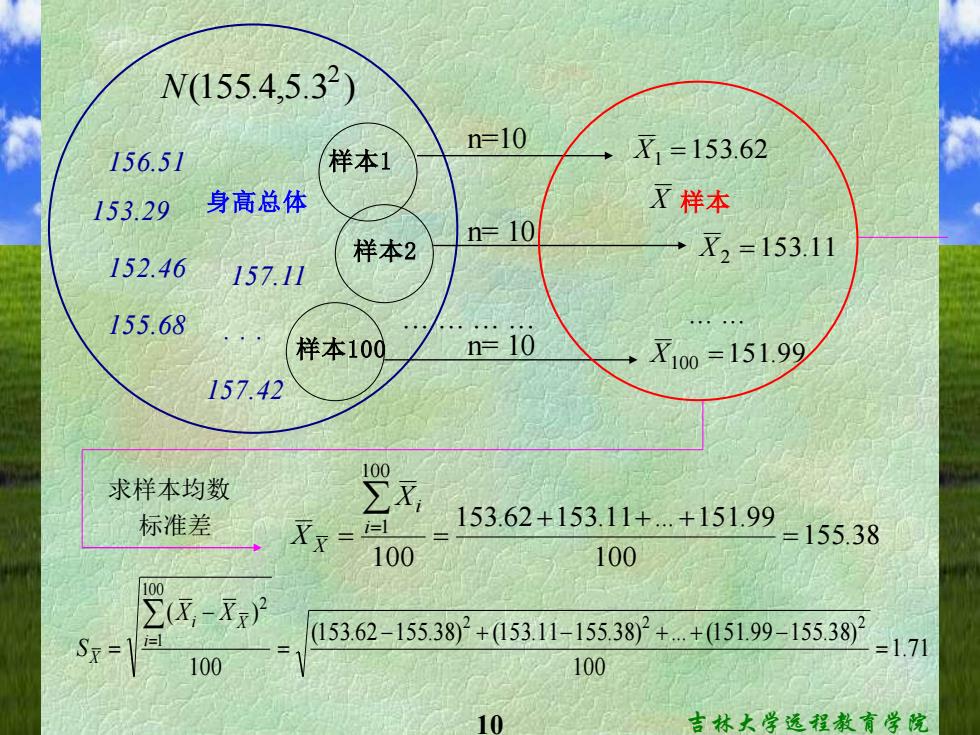
N155.4,5.32) n=10 156.51 样本1 X1=153.62 153.29 身高总体 了样本 n=10 X2=153.11 152.46 样本2 157.11 155.68 样本100 n=10 →X100=151.99 157.42 求样本均数 100 x 标准差 XX=- 153.62+153.11+.+151.9 100 100 2=15538 - 5362-15382+1531-15538++05199-1538=171 100 100 10 吉林大学远程教育学院
10 吉林大学远程教育学院 (155.4,5.3 ) 2 N 身高总体 X1 =153.62 157.11 152.46 156.51 155.68 153.29 157.42 . . . 样本1 n=10 样本2 样本100 ... ... ... ... X2 =153.11 X100 =151.99 ... ... X 样本 n= 10 n= 10 求样本均数 标准差 155.38 100 153.62 153.11 ... 151.99 100 100 1 = + + + = = i= i X X X 1.71 100 (153.62 155.38) (153.11 155.38) ... (151.99 155.38) 100 ( ) 2 2 2 100 1 2 = − + − + + − = − = i= i X X X X S

编制频数表 绘直方图 抽样次数增大 W(155.4,1.682 抽样次数→o 11 吉林大学远程教育学院
11 吉林大学远程教育学院 抽样次数增大 抽样次数→ (155.4,1.68 ) 2 N 编制频数表 绘直方图