
附 二项分布 1.二项分布的定义 如果一种过程(随机实验)的结局只能是相 互对立的两种结果中的一种,例如射击的命中与 未中、治疗的有效与无效、实验动物染毒后的生 存与死亡等等,其中一种结果发生的可能性(概 率)为一常数π,被观察的n个观察单位的结局之 间相互独立,记录个观察单位中发生某一种结 果的频数X,则称随机变量X服从二项分布 吉林大学远程教育学院
2 吉林大学远程教育学院 附 二项分布 1.二项分布的定义 如果一种过程(随机实验)的结局只能是相 互对立的两种结果中的一种,例如射击的命中与 未中、治疗的有效与无效、实验动物染毒后的生 存与死亡等等,其中一种结果发生的可能性(概 率)为一常数π,被观察的n个观察单位的结局之 间相互独立,记录n个观察单位中发生某一种结 果的频数X,则称随机变量X 服从二项分布

(Binomial distribution)。常记x~B(n,π)。二 项分布属于离散型分布。 2.二项分布的概率 p(X)=CX(1-πy”Xπ' X=0,1,2,,n 其中 C= XI(n-X! 3.二项分布的图形 在应用中,常通过形如下图的图形表达(或描 述)二项分布变量的分布状况。 吉林大学远程教育学院
3 吉林大学远程教育学院 (Binomial distribution)。常记X ~ B(n,π)。二 项分布属于离散型分布。 2.二项分布的概率 ( ) X n X X p X Cn − ( ) = 1− X = 0,1,2,..., n 其中 !( )! ! X n X n C X n − = 3.二项分布的图形 在应用中,常通过形如下图的图形表达(或描 述)二项分布变量的分布状况
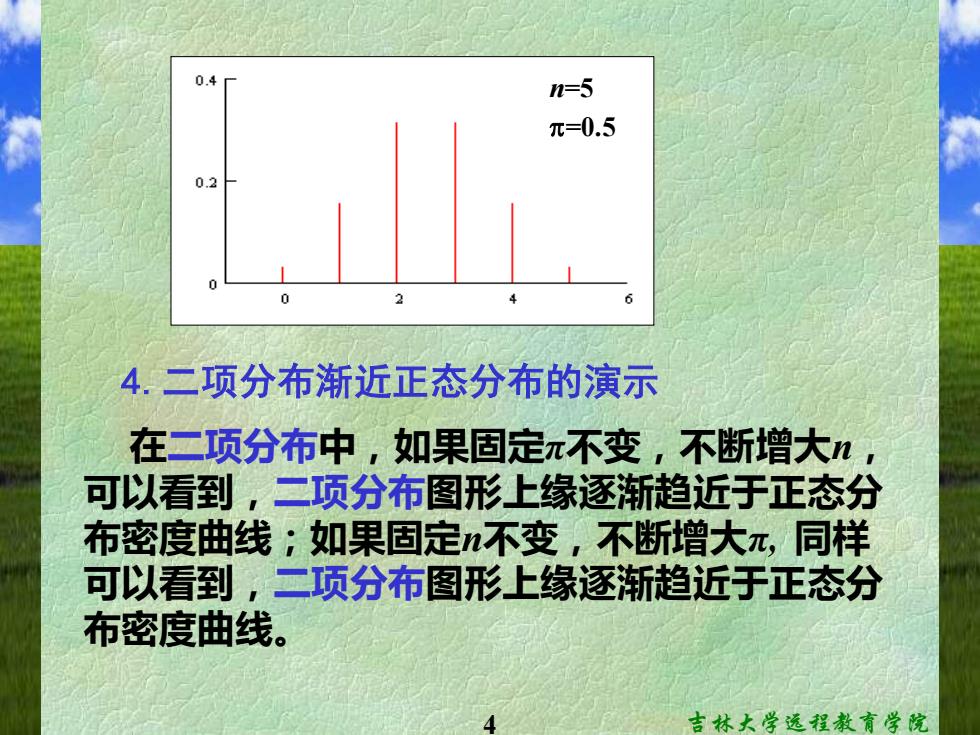
0.4 n=5 元=0.5 02 4.二项分布渐近正态分布的演示 在二项分布中,如果固定π不变,不断增大n, 可以看到,二项分布图形上缘逐渐趋近于正态分 布密度曲线;如果固定不变,不断增大π,同样 可以看到,二项分布图形上缘逐渐趋近于正态分 布密度曲线。 吉林大学远程散育学院
4 吉林大学远程教育学院 n=5 =0.5 4.二项分布渐近正态分布的演示 在二项分布中,如果固定π不变,不断增大n, 可以看到,二项分布图形上缘逐渐趋近于正态分 布密度曲线;如果固定n不变,不断增大π, 同样 可以看到,二项分布图形上缘逐渐趋近于正态分 布密度曲线
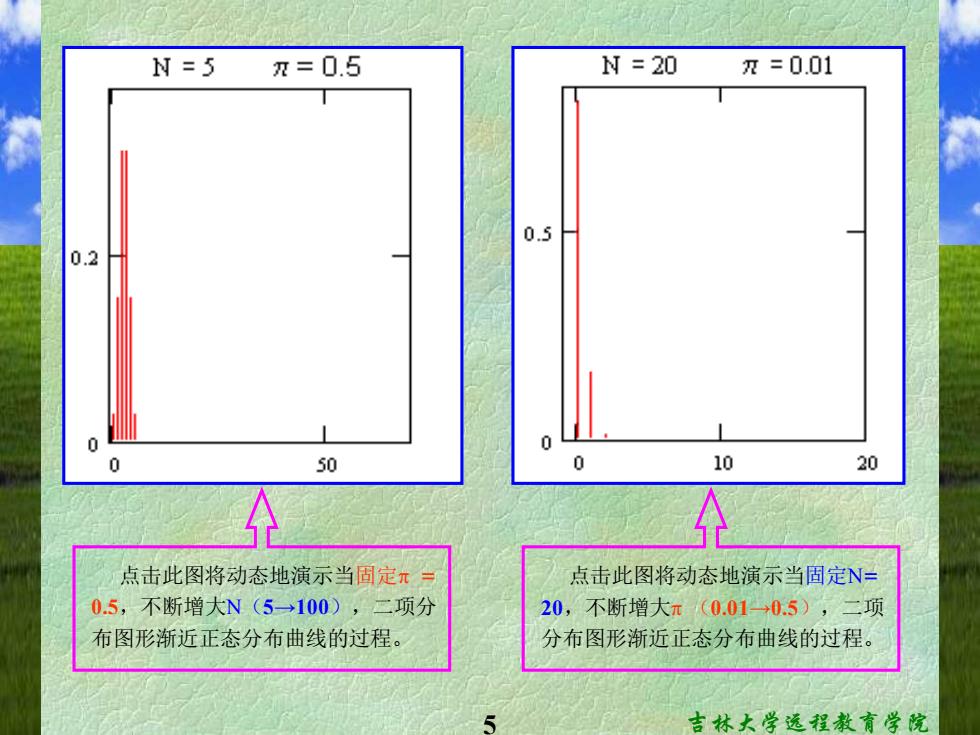
N=5 π=0.5 N=20 π=0.01 0.5 0.2 0 50 10 20 点击此图将动态地演示当固定π 点击此图将动态地演示当固定N 0.5,不断增大N(5→100),二项分 20,不断增大π(0.01→0.5),二项 布图形渐近正态分布曲线的过程。 分布图形渐近正态分布曲线的过程。 吉林大学远程教育学院
5 吉林大学远程教育学院 点击此图将动态地演示当固定 = 0.5,不断增大N(5→100),二项分 布图形渐近正态分布曲线的过程。 点击此图将动态地演示当固定N= 20,不断增大 (0.01→0.5),二项 分布图形渐近正态分布曲线的过程

5.二项分布的正态近似条件 在应用中,当π或1-π不太小,而足够大,如 p和(p≥5,我们常用正态近似原理来处理二项 分布的问题,此为二项分布的正态近似条住。在实 际中,可用p估计π。 6.二项分布的均数与标准差 均数 l=nπ 标准差 o=/nπ(1-π) 吉林大学远程教育学院
6 吉林大学远程教育学院 5.二项分布的正态近似条件 在应用中,当π或1-π不太小,而n足够大,如 np和n(1-p)≥5,我们常用正态近似原理来处理二项 分布的问题,此为二项分布的正态近似条件。在实 际中,可用p 估计π。 6.二项分布的均数与标准差 均数 标准差 = n = n(1−)

如果用率表示,则为: lp=π π(1-π) n 附例据以往经验新性儿染色体异常率为0.01,某研究者想了解 当地新生儿染色体异常是否低于一般,随机抽查当地400名新生儿, 结果1名染色体异常。请作统计推断。 本例n=400,X=1<5,不满足正态近似条件, 故不能用率的检验。 吉林大学远程教育学院
7 吉林大学远程教育学院 如果用率表示,则为: p = n p (1 ) − = 附例 据以往经验新生儿染色体异常率为0.01,某研究者想了解 当地新生儿染色体异常是否低于一般,随机抽查当地400名新生儿, 结果1名染色体异常。请作统计推断。 本例n=400,X=1<5,不满足正态近似条件, 故不能用率的u检验

本例若假设当地新生儿染色体异常率与一般的 新生儿染色体异常率πo=0.01相等,即在H。: π=π0=0.01成立的条件下,本次抽样得到的染色体 异常人数X服从二项分布B(400,0.01)。 根据研究目的,只问当地新生儿染色体异常 率是否低于一般,故为单侧检验。按照二项分布 的概率计算公式,需计算事件“X≤1”的概率。 H0:π=π0=0.01 0a=0.05 H1:π<0.01 吉林大学远程教育学院
8 吉林大学远程教育学院 本例若假设当地新生儿染色体异常率π与一般的 新生儿染色体异常率π0=0.01相等,即在H0 : π=π0=0.01成立的条件下,本次抽样得到的染色体 异常人数X服从二项分布B(400,0.01)。 根据研究目的,只问当地新生儿染色体异常 率是否低于一般,故为单侧检验。按照二项分布 的概率计算公式,需计算事件“X≤1”的概率。 H0 : π=π0 = 0.01 H1 : π <0.01 α= 0.05

p(X)=C(1-π”-xπX P(X≤1)=P(X=0)+P(X=1) n 4001 X!(n-X)! 0400-0 1-0.01)40-0.019 01=1 (400-)1-0.01)-0.01 4001 =0.990+4000.990.01 4001 400.3991 400 399 3991 3991 =0.0180+0.0725=0.0905 9 吉林大学远程教育学院
9 吉林大学远程教育学院 P(X 1) = P(X = 0) + P(X =1) 400 0 0 (1 0.01) 0.01 0!(400 0)! 400! − − − = ( ) X n X X p X Cn − ( ) = 1− !( )! ! X n X n C X n − = 0!=1 400 1 1 (1 0.01) 0.01 1!(400 1)! 400! − − − + 0.99 0.01 399! 400! 0.99400 399 = + = 0.0180+0.0725 = 0.0905 400 399! 400 399! 399! 400! = =

PX≤1)=0.0905>0.05,按a=0.05水准尚不能拒 绝H,,差异无统计学意义。尚不能认为该地新生 儿染色体异常率低于一般新生儿。 从上面的例题可以看出利用二项分布的理论方 法作二项分类资料的统计推断,当很大时,其概 率计算非常繁复。实际当中,可利用二项分布的 Poisson分布近似性质,当n很大且π很小时,用 Poisson分布的概率计算近似替代二项分布的概率 计算(参见相关的统计专业书籍)。 10 吉林大学远程教育学院
10 吉林大学远程教育学院 P(X≤1)=0.0905>0.05,按α=0.05水准尚不能拒 绝H0,差异无统计学意义。尚不能认为该地新生 儿染色体异常率低于一般新生儿。 从上面的例题可以看出利用二项分布的理论方 法作二项分类资料的统计推断,当n很大时,其概 率计算非常繁复。实际当中,可利用二项分布的 Poisson分布近似性质,当n很大且π很小时,用 Poisson分布的概率计算近似替代二项分布的概率 计算(参见相关的统计专业书籍)

第四节2检验 对于分类变量资料的假设检验,前面我们学习了 率的检验,此方法只适用于两组以内的样本率的 比较,并且样本率需要满足正态近似条件。对于多 组(两组以上)样本率或构成比的比较,不能用率 的检验两两进行比较,需要用x检验。 x2检验(chi-square test)是分类变量资料中最常 用、用途较广的假设检验方法。它不但可以推断两 个及多个总体率或总体构成比之间的差异,而且还 可检验两种属性或两个变量之间有无关联性, 吉林大学远程教育学院
11 吉林大学远程教育学院 对于分类变量资料的假设检验,前面我们学习了 率的u检验,此方法只适用于两组以内的样本率的 比较,并且样本率需要满足正态近似条件。对于多 组(两组以上)样本率或构成比的比较,不能用率 的u检验两两进行比较,需要用χ 2检验。 第四节 χ 2 检验 χ 2检验(chi-square test)是分类变量资料中最常 用、用途较广的假设检验方法。它不但可以推断两 个及多个总体率或总体构成比之间的差异,而且还 可检验两种属性或两个变量之间有无关联性