
第八节 方差分析 二、完全随机设计的单因素方差分析 按照完全随机化原则将受试对象分配到只有一 个研究因素(或处理因素)的多个水平中,通过 比较此多个水平分组的样本均数来推断研究因素 的总体效应。此方法称为单因素方差分析 (one-way ANOVA)。 2 吉林大学远程教有学院
2 吉林大学远程教育学院 二、完全随机设计的单因素方差分析 按照完全随机化原则将受试对象分配到只有一 个研究因素(或处理因素)的多个水平中,通过 比较此多个水平分组的样本均数来推断研究因素 的总体效应。此方法称为单因素方差分析 (one-way ANOVA)。 第八节 方差分析
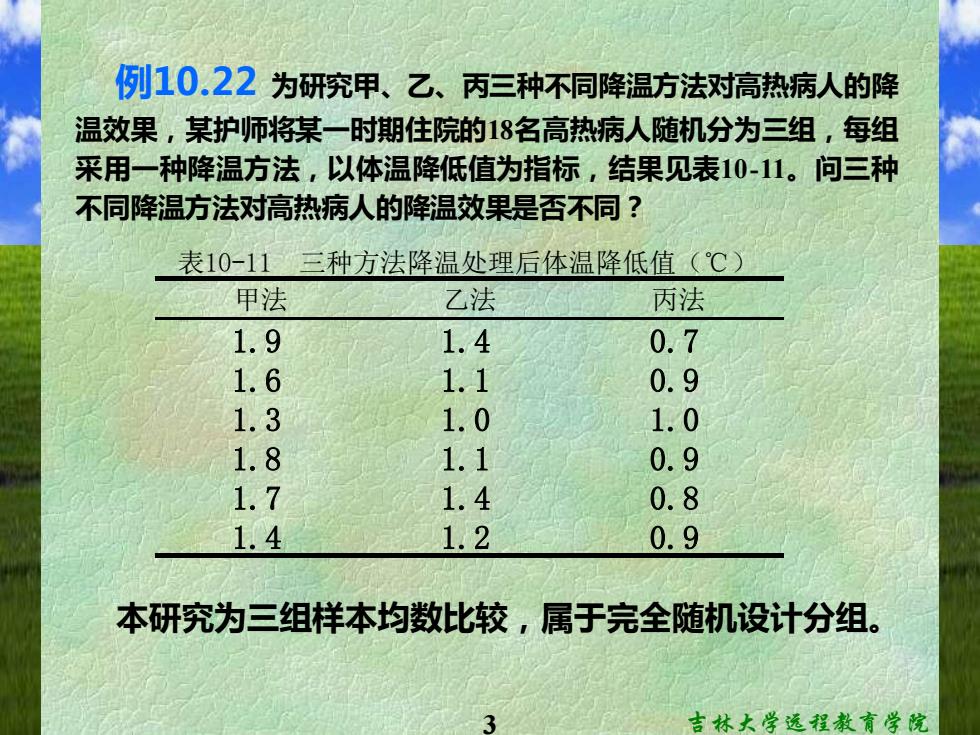
例10.22为研究甲、乙、丙三种不同降温方法对高热病人的降 温效果,某护师将某一时期住院的18名高热病人随机分为三组,每组 采用一种降温方法,以体温降低值为指标,结果见表10-11。问三种 不同降温方法对高热病人的降温效果是否不同? 表10-11 三种方法降温处理后体温降低值(℃) 甲法 乙法 丙法 1.9 1.4 0.7 1.6 1.1 0.9 1.3 1.0 1.0 1.8 1.1 0.9 1.7 1.4 0.8 1.4 1.2 0.9 本研究为三组样本均数比较,属于完全随机设计分组。 吉林大学远程教育学院
3 吉林大学远程教育学院 例10.22 为研究甲、乙、丙三种不同降温方法对高热病人的降 温效果,某护师将某一时期住院的18名高热病人随机分为三组,每组 采用一种降温方法,以体温降低值为指标,结果见表10-11。问三种 不同降温方法对高热病人的降温效果是否不同? 本研究为三组样本均数比较,属于完全随机设计分组。 甲法 乙法 丙法 1.9 1.4 0.7 1.6 1.1 0.9 1.3 1.0 1.0 1.8 1.1 0.9 1.7 1.4 0.8 1.4 1.2 0.9 表10-11 三种方法降温处理后体温降低值(℃)

本例题作方差分析的步骤如下: 1.建立检验假设和确定检验水准 H0:甲=z=丙 H:4甲、乙、炳不等或不全相等 0=0.05 2.计算F值 通过下面表10-12所列计算公式求得F值。 吉林大学远程教育学院
4 吉林大学远程教育学院 本例题作方差分析的步骤如下: H0 : μ甲=μ乙=μ丙 H1 : μ甲、μ乙、μ丙不等或不全相等 α= 0.05 ⒈ 建立检验假设和确定检验水准 ⒉ 计算F 值 通过下面表10-12所列计算公式求得F值

表10-12完全随机设计的单因素方差分析的计算公式 变异来源 离均差平方和 自由度 均方 SS 人 MS F值 (?X) 组间(处理) k-1 SS组向/V组间 n MS组同/MS组内 组内(误差) SS总-SS组间 N-k SS组内/V组内 总 ?X2-C N-1 *C=(?X)21N 通过下面表10-11下半部的计算结果代入上述公 式可求得F值。 吉林大学远程教育学院
5 吉林大学远程教育学院 变异来源 离均差平方和 SS 均方 MS F 值 组间(处理) 组内(误差) 总 表10-12 完全随机设计的单因素方差分析的计算公式 自由度 ν * 2 ( ) C n X i i j ij ? - ? 2 * ? X - C SS总 - SS组间 k -1 N - k N -1 SS组间 /n 组间 SS组内 /n 组内 MS组间 / MS组内 *C ( X ) / N 2 = ? 通过下面表10-11下半部的计算结果代入上述公 式可求得F值
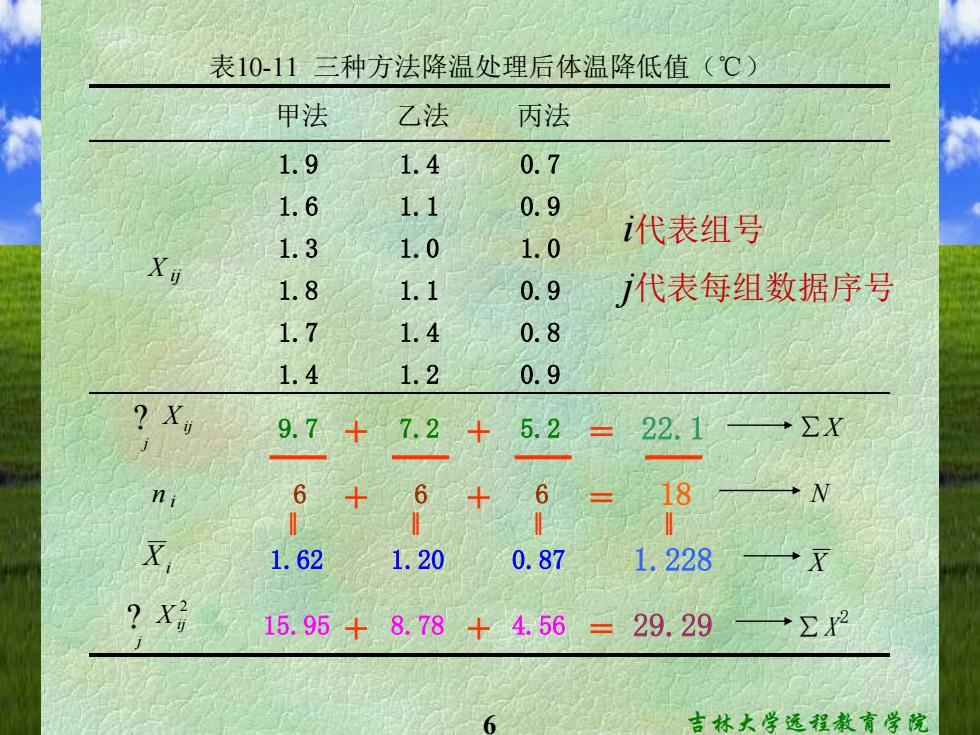
表10-11三种方法降温处理后体温降低值(℃) 甲法 乙法 丙法 1.9 1.4 0.7 1.6 1.1 0.9 X可 1.3 1.0 1.0 代表组号 1.8 1.1 0.9 代表每组数据序号 1.7 1.4 0.8 1.4 1.2 0.9 ?X, 9.7+72+5.2 = 22.1 ∑X ni 6+ +6= 18 N x 1.62 1.20 0.87 1.228 ? 15.95+8.78 +4.56=29.29 ∑2 吉林大学远程教育学院
6 吉林大学远程教育学院 甲法 乙法 丙法 1.9 1.4 0.7 1.6 1.1 0.9 1.3 1.0 1.0 1.8 1.1 0.9 1.7 1.4 0.8 1.4 1.2 0.9 9.7 7.2 5.2 22.1 ∑X n i 6 6 6 18 N 1.62 1.20 0.87 1.228 15.95 8.78 4.56 29.29 ∑X 2 表10-11 三种方法降温处理后体温降低值(℃) X ij ? j Xij Xi X ? j Xij 2 + + = + + = + + = ‖ ‖ ‖ ‖ i代表组号 j代表每组数据序号
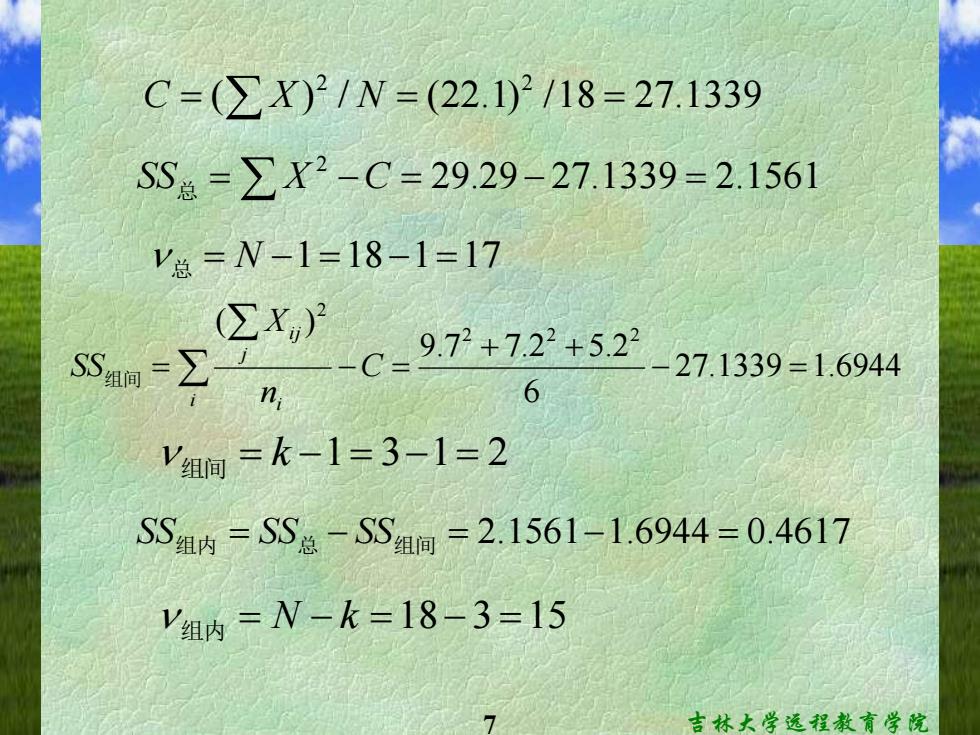
C=(∑X)21N=(22.1)2118=27.1339 SSa=∑X2-C-29.29-27.1339=2.1561 V总=N-1=18-1=17 (∑X)} SSa陶=∑I -C-9,72+722+52-27.1339=16944 n 6 V组向=k-1=3-1=2 SS组内=SSa-SS组▣=21561-1.6944=0.4617 Y组内=W-k=18-3=15 7 吉林大学远程教育学院
7 吉林大学远程教育学院 ( ) / (22.1) /18 27.1339 2 2 C = X N = = = - = 29.29 - 27.1339 = 2.1561 2 SS总 X C n 总 = N -1=18-1=17 27.1339 1.6944 6 9.7 7.2 5.2 ( ) 2 2 2 2 - = + + = - = C n X SS i i j i j 组间 n 组间 = k -1= 3-1= 2 SS组内 = SS总 - SS组间 = 2.1561-1.6944 = 0.4617 n 组内 = N - k =18-3 =15
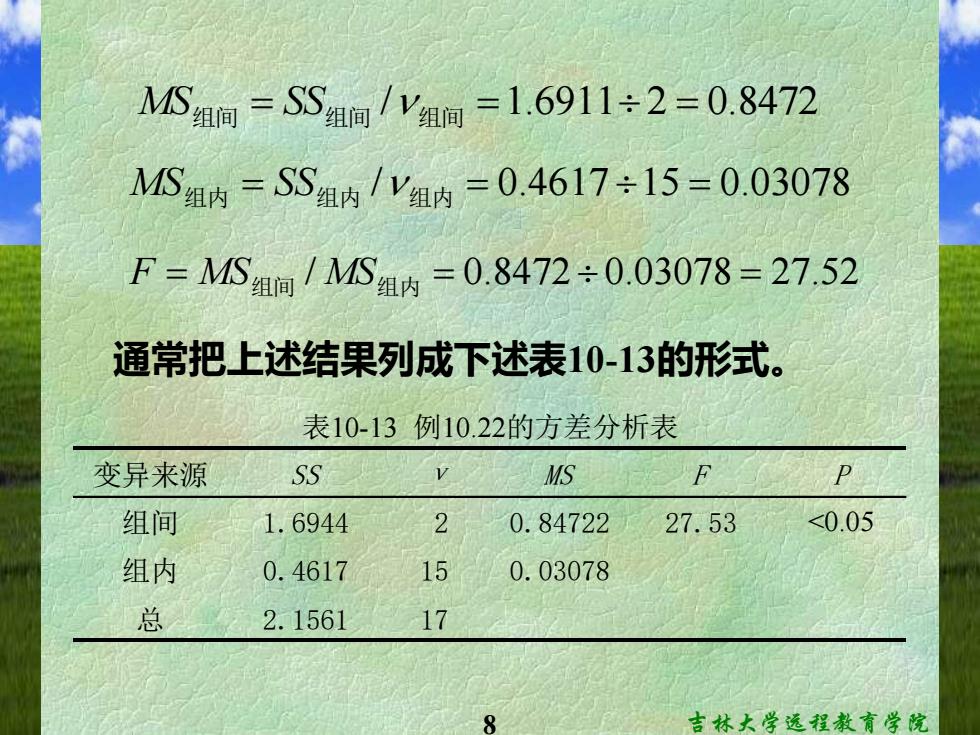
MS组间=SS组▣1V组▣=1.6911÷2=0.8472 MS组内=SS组内/y组内=0.4617÷15=0.03078 F=MS组▣/MS组内=0.8472÷0.03078=27.52 通常把上述结果列成下述表10-13的形式。 表10-13例10.22的方差分析表 变异来源 SS MS F P 组间 1.6944 2 0.84722 27.53 <0.05 组内 0.4617 15 0.03078 总 2.1561 17 8 吉林大学远程教育学院
8 吉林大学远程教育学院 MS组间 = SS组间 /n 组间 =1.69112 = 0.8472 MS组内 = SS组内 /n 组内 = 0.4617 15 = 0.03078 F = MS组间 / MS组内 = 0.8472 0.03078 = 27.52 通常把上述结果列成下述表10-13的形式。 变异来源 SS MS F P 组间 1.6944 2 0.84722 27.53 <0.05 组内 0.4617 15 0.03078 总 2.1561 17 表10-13 例10.22的方差分析表 ν

3.确定P值和作出推断结论 由a=0.05,4=组间=2,2=组内=15,查 附表3,得F)=F0s215)=3.68,今求得 F-27.52>3.68,则P<0.05,按a=0.05水准拒绝 H。,有统计学意义。可认为三种不同降温方法 效果总体不同或不全相同。 通过附图理解上述P值大小的确定。 若要了解哪些组之间有差别,哪些组之间无差别 ,需要进一步作多重比较(详后)。 吉林大学远程教育学院
9 吉林大学远程教育学院 ⒊ 确定P 值和作出推断结论 由α=0.05,ν1=ν组间=2,ν2=ν组内=15,查 附表3 ,得 ,今求得 F=27.52>3.68,则P<0.05,按α=0.05水准拒绝 H0,有统计学意义。可认为三种不同降温方法 效果总体不同或不全相同。 ( , ) 0.0 5(2,1 5) 3.68 1 2 F n n = F = 若要了解哪些组之间有差别,哪些组之间无差别 ,需要进一步作多重比较(详后)。 通过附图理解上述P值大小的确定

三、配伍组设计的双因素方差分析 配伍组设计(亦称随机区组设计)是配对设计 的扩展,同样选择对研究结果有影响的非研究因 素相同或相近的受试对象配成伍(或称区组), 每个配伍组内的受试对象(两个以上)接受不同 的处理的试验设计方法。此方法主要用于控制受 试对象的个体差异对实验效应的影响。 10 吉林大学远程教育学院
10 吉林大学远程教育学院 三、配伍组设计的双因素方差分析 配伍组设计(亦称随机区组设计)是配对设计 的扩展,同样选择对研究结果有影响的非研究因 素相同或相近的受试对象配成伍(或称区组), 每个配伍组内的受试对象(两个以上)接受不同 的处理的试验设计方法。此方法主要用于控制受 试对象的个体差异对实验效应的影响

配伍组设计的多个(两个以上)样本均数的比较 可用两因素方差分析(two-way ANOVA)。两因素 是指研究因素(或处理因素)和配伍因素。 此方法的基本原理是将总变异分解为处理组间变 异、配伍组(区组)间变异和误差三个部分。上述 四种变异有以下关系: SS总=SS处理+SS区组+SS误差 V总=处理+区组+保差 与单因素方差分析相比,由于从误差变异中分 11 吉林大学远程教育学院
11 吉林大学远程教育学院 配伍组设计的多个(两个以上)样本均数的比较 可用两因素方差分析(two-way ANOVA)。两因素 是指研究因素(或处理因素)和配伍因素。 此方法的基本原理是将总变异分解为处理组间变 异、配伍组(区组)间变异和误差三个部分。上述 四种变异有以下关系: SS总 = SS处理+ SS区组+ SS误差 ν总 = ν处理+ ν区组+ ν误差 与单因素方差分析相比,由于从误差变异中分