
第十二章非参数统计 第四节 配伍组设计的秩和检验 (Friedman检验 一、处理组间的比较 二、X分布近似法 当配伍组数b或处理组数超出M界值表的范围 时,可以采用近似x分布法,按下式计算。 吉林大学远程教育学院
2 吉林大学远程教育学院 当配伍组数b或处理组数k超出M界值表的范围 时,可以采用近似χ 2分布法,按下式计算。 二、χ 2分布近似法 第十二章 非参数统计 第四节 配伍组设计的秩和检验 (Friedman检验) 一、处理组间的比较

12 公式(12.9) bk(k+1) (∑T)-3b(k+0 式中b为区组数,为处理组数,T为各处理组对应的秩 和,x统计量对应的自由度为k-1。 例12.8以例12.7的资料简述其分析步骤。 k=4,b=7,T1=9,T2=27,T3=21,T4=13 6nE浙) 7x4x4+D9+27+212+13)-3×74+) 12 =16.71 吉林大学远程教育学院
3 吉林大学远程教育学院 − + + = ( ) 3 ( 1) ( 1) 2 12 2 T b k bk k i 公式(12.9) 式中b为区组数,k为处理组数,Tj为各处理组对应的秩 和,χ 2统计量对应的自由度为k-1。 k=4,b =7,T1=9,T2=27,T3=21,T4=13 例12.8 以例12.7的资料简述其分析步骤。 − + + = ( ) 3 ( 1) ( 1) 2 12 2 T b k bk k i (9 27 21 13 ) 3 7 (4 1) 7 4 (4 1) 12 2 2 2 2 + + + − + + = =16.71

查2界值表xaw-Xo.05B=7.81,今求得X2= 16.71>7.81,故P<0.05,按a=0.05水准拒绝H0。 认为治疗前后四个阶段患者的$GPT不同或不全 相同。 当各区组间相同的秩次较多时,需对公式(12.9) 进行校正。 x2=x2/C C=1-∑G-t,)/bkk2-) 公式(12.10) 式中为各区组内第个具有相同秩次的个数,b、k分别 代表区组数和处理组数。 吉林大学远程教育学院
4 吉林大学远程教育学院 查χ 2界值表χ 2 α(ν)=χ 2 0.05(3)=7.81,今求得χ 2 = 16.71>7.81 ,故P<0.05,按α=0.05水准拒绝H0。 认为治疗前后四个阶段患者的SGPT不同或不全 相同。 公式(12.10) 式中t j为各区组内第j 个具有相同秩次的个数,b、k 分别 代表区组数和处理组数 。 当各区组间相同的秩次较多时,需对公式(12.9) 进行校正。 c /C 2 2 = =1−( − )/ ( −1) 3 2 C t t bk k j j

三、配伍组设计资料的两两比较 1.先将各处理组的秩和由小到大排列,再按顺 序列出各对比组及每个对比组的组间跨度。 2.求检验统计量g,公式见下: 9= TA-TB 公式(12.11) STA-TE bk(k+1) STA-Ta 12 式中T4,TB为两个对比组的秩和 ,S,是其对应的标准 误,b、k分别代表区组数和处理组数。 吉林大学远程散育学院
5 吉林大学远程教育学院 三、配伍组设计资料的两两比较 1. 先将各处理组的秩和由小到大排列,再按顺 序列出各对比组及每个对比组的组间跨度a。 2. 求检验统计量q,公式见下: TA TB A B S T T q − − = 公式(12.11) 12 ( +1) − = bk k STA TB 式中TA、TB为两个对比组的秩和, 是其对应的标准 误,b、k 分别代表区组数和处理组数 。 TA TB S −

3.确定P值和作出推断结论,查g界值表(v= o),见教材后附表5,即qa(e,a)。当求得q≥ qa(e,a)时,按a检验水准拒绝H,两对比组 间差别有统计学意义;反之,尚不拒绝H。 例12.9对例12.7资料作多重比较。 ①检验假设 H0:治疗前后四个阶段患者的SGPT的任两个比较组总体分布相同 H1:治疗前后四个阶段患者的SGPT的任两个比较组总体分在 不同或不全相同 =0.05 吉林大学远程教育学院
6 吉林大学远程教育学院 3. 确定P值和作出推断结论,查q界值表(ν = ∞),见教材后附表5,即qα(∞,a)。当求得 q ≥ qα(∞ ,a) 时,按α检验水准拒绝H0,两对比组 间差别有统计学意义;反之,尚不拒绝H0。 例12.9 对例12.7资料作多重比较。 H0 : 治疗前后四个阶段患者的SGPT的任两个比较组总体分布相同 H1 : 治疗前后四个阶段患者的SGPT的任两个比较组总体分布 不同或不全相同 ① 检验假设 α= 0.05
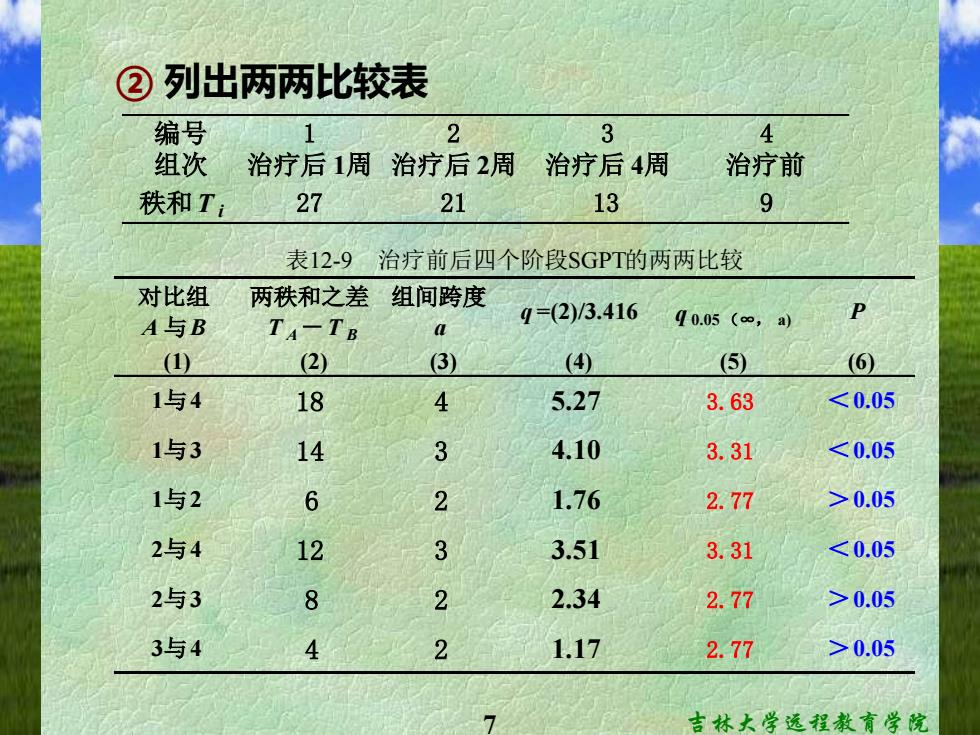
②列出两两比较表 编号 2 3 4 组次 治疗后1周治疗后2周 治疗后4周 治疗前 秩和T 27 21 13 9 表12-9治疗前后四个阶段SGPT的两两比较 对比组 两秩和之差 组间跨度 A与B TA-TB q=(2)/3.416 q0.05(∞,a (1) 2) 3) (④) ⑤) (6) 1与4 18 4 5.27 3.63 0.05 2与4 12 3 3.51 3.31 0.05 3与4 4 2 1.17 2.77 >0.05 7 吉林大学远程教育学院
7 吉林大学远程教育学院 ② 列出两两比较表 编号 1 2 3 4 组次 治疗后 1周 治疗后 2周 治疗后 4周 治疗前 秩和T i 27 21 13 9 对比组 两秩和之差 组间跨度 A 与B T A-T B a (1) (2) (3) (4) (5) (6) 1与4 18 4 5.27 3.63 <0.05 1与3 14 3 4.10 3.31 <0.05 1与2 6 2 1.76 2.77 >0.05 2与4 12 3 3.51 3.31 <0.05 2与3 8 2 2.34 2.77 >0.05 3与4 4 2 1.17 2.77 >0.05 q =(2)/3.416 q 0.05(∞, a) P 表12-9 治疗前后四个阶段SGPT的两两比较

③计算检验统计量 按公式(12.11)计算检验 统计量q。 bk(k+1) 7×4×(4+1)=3.416 12 12 计算1与4组的q值为: 9 TA-TB 18 =5.27 ST-TB 3.416 仿此可得其它值,见表12-9中的④。 ④确定P值和作出推断结论 查g界值表(y= ∞),见表12-9中的⑤)。得P值,见表12-9中的6. 8 吉林大学远程教有学院
8 吉林大学远程教育学院 计算1与4组的q 值为: ③ 计算检验统计量 按公式(12.11)计算检验 统计量q 。 3.416 12 7 4 (4 1) 12 ( 1) = + = + − = bk k STA TB 5.27 3.416 18 = = − = TA −TB A B S T T q 仿此可得其它q 值,见表12-9中的(4)。 ④ 确定P值和作出推断结论 查q界值表(ν = ∞),见表12-9中的(5)。得P值,见表12-9中的(6)

在a=0.05水准上,可认为治疗后一周与治疗 前、治疗后一周与治疗后四周、治疗后两周 与治疗前的SGPT有统计学差异,其余各组间 无统计学差异。 吉林大学远程教育学院
9 吉林大学远程教育学院 在α=0.05水准上,可认为治疗后一周与治疗 前、治疗后一周与治疗后四周、治疗后两周 与治疗前的SGPT有统计学差异,其余各组间 无统计学差异

第十三章 回归与相关 第一节 直线回归 一、直线回归的概念 直线回归(linear regression)是描述两个变量 间依存关系的一种统计分析方法。此法又称简单 回归(simple regression)。此法通过直线回归方 程(linear regression equation)描述一个变量YI常 称为应变量(dependent variable)]依存另一个变 量X[常称为自变量(independent variable)]变化 10 吉林大学远程教育学院
10 吉林大学远程教育学院 第十三章 回归与相关 一、直线回归的概念 直线回归(linear regression)是描述两个变量 间依存关系的一种统计分析方法。此法又称简单 回归(simple regression)。此法通过直线回归方 程(linear regression equation)描述一个变量Y[常 称为应变量(dependent variable)]依存另一个变 量X[常称为自变量(independent variable)]变化 第一节 直线回归

的数量关系。由此方程可确定一条回归直线。 二、直线回归方程的求法 直线回归方程的表达式为 Y=a+bx 公式(13.1) 式中X为自变量,为应变量的估计值,a为 回归直线在轴上的截距(intercept),b为回归系 数(regression coefficient),也即回归直线的斜率 (slope)。根据数学上的最小二乘法的原理计算a 和b。计算公式如下: 11 吉林大学远程教育学院
11 吉林大学远程教育学院 的数量关系。由此方程可确定一条回归直线。 二、直线回归方程的求法 直线回归方程的表达式为 Y ˆ = a +bX 公式(13.1) 式中X为自变量, 为应变量Y的估计值,a 为 回归直线在Y轴上的截距(intercept),b为回归系 数(regression coefficient),也即回归直线的斜率 (slope)。根据数学上的最小二乘法的原理计算a 和b 。计算公式如下: Y ˆ