
第十二章 非参数统计 第三节 成组设计多个样本比较的 秩和检验 (Kruskal-Vallis法) 二、秩和检验后的两两比较 多组设计资料,经秩和检验后,若拒绝H0,则 意味着各组样本指标所代表的总体指标间不同或 不全相同。当要了解任意两总体指标间是否存在 差别时,需做多组样本间的多重比较。 吉林大学远程散育学院
2 吉林大学远程教育学院 二、秩和检验后的两两比较 多组设计资料,经秩和检验后,若拒绝H0,则 意味着各组样本指标所代表的总体指标间不同或 不全相同。当要了解任意两总体指标间是否存在 差别时,需做多组样本间的多重比较。 第十二章 非参数统计 第三节 成组设计多个样本比较的 秩和检验 (Kruskal-Wallis 法)

多重比较的方法很多。这里介绍一种推广的 检验,本法不仅适用于例数相等,也适用于例数 不等的情况。检验统计量1按下式计算: Ta-T8 N(N+IXN-1-H(11) 公式(12.7 12(N-k) nA nB 式中T,为屣意两比较组A与B的平均秩和,n4,ng为各 组样本含量,k为处理组数,N为处理组的总例数 H为秩和检验中算得的统计量H或H。,t值的自由度为 N-k。 吉林大学远程教育学院
3 吉林大学远程教育学院 多重比较的方法很多。这里介绍一种推广的 t 检验,本法不仅适用于例数相等,也适用于例数 不等的情况。检验统计量t 按下式计算: ) 1 1 ( 12( ) ( 1)( 1 ) A B A B N k n n N N N H T T t + − + − − − = 公式(12.7) 式中 为任意两比较组A与B的平均秩和,nA 、 nB为各 组样本含量,k 为处理组数,N 为处理组的总例数, H 为秩和检验中算得的统计量H 或Hc,t 值的自由度为 N-k 。 TA、TB

例12.5以例12.4的资料说明该检验方法的分析步骤。 ① 检验假设 H0:两比较组血浆总皮质醇含量总体分布相同 H:两比较组血浆总皮质醇含量总体分布不同 0=0.05 ②计算各比较组平均秩和用工计算。 T=9.65,T=11.75,T=25.1. ③两两比较利用公式(12.7)通过下表12-5计算得 出任意两处理组间的比较结果。 吉林大学远程教育学院
4 吉林大学远程教育学院 例12.5 以例12.4的资料说明该检验方法的分析步骤。 H0 : 两比较组血浆总皮质醇含量总体分布相同 H1 : 两比较组血浆总皮质醇含量总体分布不同 ① 检验假设 α= 0.05 ② 计算各比较组平均秩和 用 计算。 i i i n T T = T1 = 9.65,T2 =11.75,T3 = 25.1。 ③ 两两比较 利用公式(12.7)通过下表12-5计算得 出任意两处理组间的比较结果
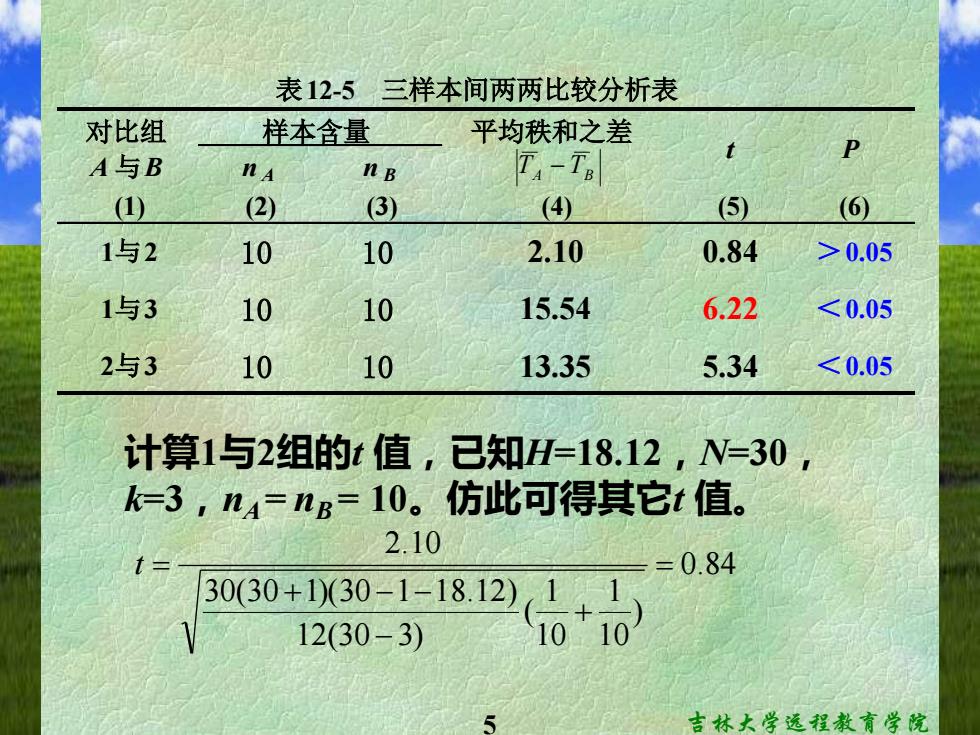
表12-5三样本间两两比较分析表 对比组 样本含量 平均秩和之差 P A与B nA nB Ta-Ta t (1) (2) (3) (4) (⑤) (6) 1与2 10 10 2.10 0.84 >0.05 1与3 10 10 15.54 6.22 <0.05 2与3 10 10 13.35 5.34 <0.05 计算1与2组的t值,已知H=18.12,N=30, =3,n4=ng=10。仿此可得其它t值。 2.10 =0.84 808g(00 12(30-3) 吉林大学远程教育学院
5 吉林大学远程教育学院 对比组 平均秩和之差 A 与B n A n B (1) (2) (3) (4) (5) (6) 1与2 10 10 2.10 0.84 >0.05 1与3 10 10 15.54 6.22 <0.05 2与3 10 10 13.35 5.34 <0.05 表12-5 三样本间两两比较分析表 样本含量 t P TA − TB 计算1与2组的t 值,已知H=18.12,N=30, k=3,nA = nB = 10。仿此可得其它t 值。 0.84 ) 10 1 10 1 ( 12(30 3) 30(30 1)(30 1 18.12) 2.10 = + − + − − t =

④确定P值和作出推断结论查自由度为v = N-k=30-3=27的1界值表得taw=.0s27)= 2.052,与表12-5中的(5)中各项比较得出P 值。 本例各项P值见表12-5中的⑥。 在a=0.05水准上,认为正常人组与单纯性 肥胖组相比血浆总皮质醇测定值无统计学差 异,而皮质醇增多症组与正常人组、单纯性 肥胖组相比血浆总皮质醇测定值均有统计学 意义。 吉林大学远程教育学院
6 吉林大学远程教育学院 ④ 确定P值和作出推断结论 查自由度为ν = N-k=30-3=27的t 界值表得tα(ν)=t0.05(27) = 2.052,与表12-5中的(5)中各项比较得出P 值。 本例各项P值见表12-5中的(6) 。 在α=0.05水准上,认为正常人组与单纯性 肥胖组相比血浆总皮质醇测定值无统计学差 异,而皮质醇增多症组与正常人组、单纯性 肥胖组相比血浆总皮质醇测定值均有统计学 意义。 C

第十二章非参数统计 第三节 成组设计多个样本比较的 秩和检验 (Kruskal-Wallis法) 三、频数表资料的比较 例12.6 某医到师观察药物治疗慢性、亚急性、急性颈动脉炎眩 晕患者的疗效,数据见下表12-6。试分析该药物对三种类型颈动脉炎 眩晕患者的疗效有无差别? 本研究为三组样本的定性指标(疗效的四分级) 的频数表资料。 吉林大学远程教有学院
7 吉林大学远程教育学院 第十二章 非参数统计 三、频数表资料的比较 例12.6 某医师观察药物治疗慢性、亚急性、急性颈动脉炎眩 晕患者的疗效,数据见下表12-6。试分析该药物对三种类型颈动脉炎 眩晕患者的疗效有无差别? 本研究为三组样本的定性指标(疗效的四分级) 的频数表资料。 第三节 成组设计多个样本比较的 秩和检验 (Kruskal-Wallis 法)
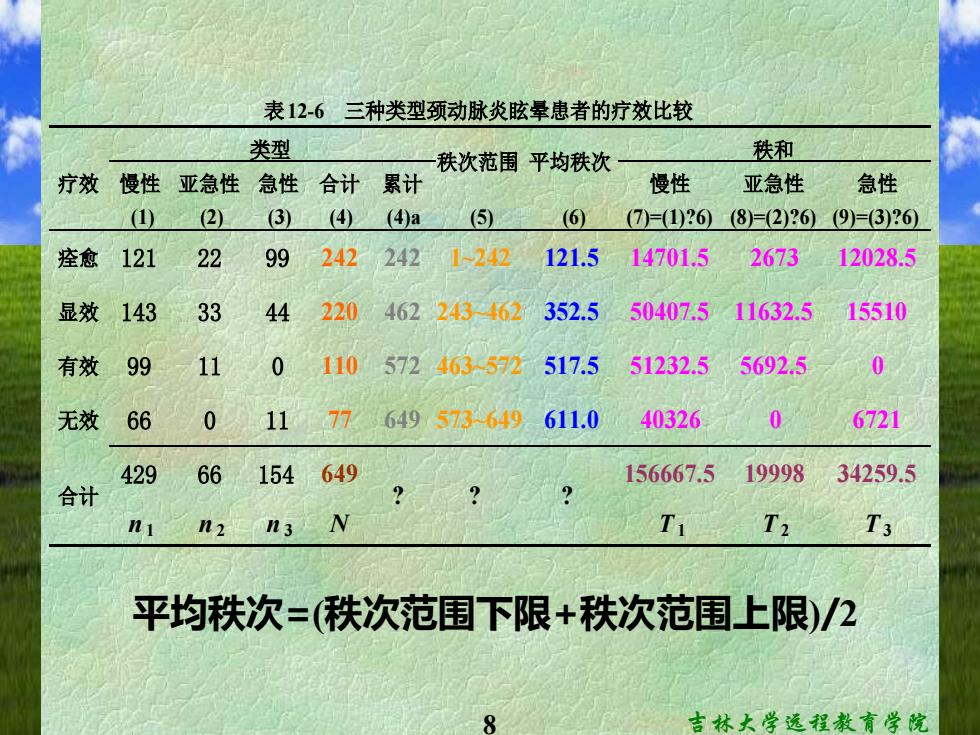
表12-6三种类型颈动脉炎眩晕患者的疗效比较 类型 秩次范围平均秩次 秩和 疗效慢性亚急性急性合计累计 慢性 亚急性 急性 (1) (2) (3)(4 (4)a (⑤ (6 (7)=(1)?6(8)=(2)?6)(9)=(3)?6) 痊愈121 22 992422421-242 121.514701.5 2673 12028.5 显效143 33 44 220462243462352.550407.5 11632.5 15510 有效99 11 0110572463-572517.551232.5 5692.5 0 无效66 0 11 77 649573649 611.0 40326 0 6721 429 66154649 156667.519998 34259.5 合计 n1 n2 n3 N T T2 T3 平均秩次=(秩次范围下限+秩次范围上限)/2 吉林大学远程教育学院
8 吉林大学远程教育学院 平均秩次=(秩次范围下限+秩次范围上限)/2 疗效 慢性 亚急性 急性 合计 累计 慢性 亚急性 急性 (1) (2) (3) (4) (4)a (5) (6) (7)=(1)?6) (8)=(2)?6) (9)=(3)?6) 痊愈 121 22 99 242 242 1~242 121.5 14701.5 2673 12028.5 显效 143 33 44 220 462 243~462 352.5 50407.5 11632.5 15510 有效 99 11 0 110 572 463~572 517.5 51232.5 5692.5 0 无效 66 0 11 77 649 573~649 611.0 40326 0 6721 429 66 154 649 156667.5 19998 34259.5 n 1 n 2 n 3 N T 1 T 2 T 3 表12-6 三种类型颈动脉炎眩晕患者的疗效比较 类型 秩次范围 平均秩次 秩和 合计 ? ? ?

本例的检验步骤如下: ①检验假设 H:三种类型颈动脉炎眩晕患者的疗效分布相同 H1:三种类型颈动脉炎眩晕患者的疗效分布不同或不全相同 =0.05 ②编秩先计算三组合计人数,见表12-6中的 (4),再确定各级别秩次范围,见表12-6中的⑤), 然后计算各级别平均秩次。见表12-6中的6)。 ③求秩和用各级别的平均秩次分别与每组的人 数相乘,可得每组在各级别的秩和,再将各级别的 秩和相加即得每组的秩和。见表12-6中的⑦Q)。 吉林大学远程教育学院
9 吉林大学远程教育学院 本例的检验步骤如下: ① 检验假设 ② 编秩 先计算三组合计人数,见表12-6中的 (4) ,再确定各级别秩次范围,见表12-6中的(5) , 然后计算各级别平均秩次。见表12-6中的(6) 。 H0 : 三种类型颈动脉炎眩晕患者的疗效分布相同 H1 : 三种类型颈动脉炎眩晕患者的疗效分布不同或不全相同 α= 0.05 ③ 求秩和 用各级别的平均秩次分别与每组的人 数相乘,可得每组在各级别的秩和,再将各级别的 秩和相加即得每组的秩和。见表12-6中的(7)~(9)

④计算检验统计量代入公式12.5计算H, 由于相同秩次较多,还需校正公式12.⑥。 w是-xwn H= 12 n 12 156667.52199982 34259.52 3(649+1) 649(649+1) 429 66 154 =66.6792 C=1-∑G-t)/w-W =1-42-242+220-20+10-110)+07-77j 6493-649 =0.902665 H.=66.679210.902665=73.87 10 吉林大学远程教育学院
10 吉林大学远程教育学院 ④ 计算检验统计量 代入[公式(12.5)]计算H, 由于相同秩次较多,还需校正[公式(12.6)]。 C = −(t −t ) (N − N) j j 3 3 1 / ( ) ( ) ( ) ( ) 649 649 242 242 220 220 110 110 77 77 1 3 3 3 3 3 − − + − + − + − = − Hc = 66.6792/ 0.902665 = 73.87 − + + = ( ) 3( 1) ( 1) 12 2 N n T N N H i i 3(649 1) 154 34259.5 66 19998 429 156667.5 649(649 1) 12 2 2 2 − + + + + = = 66.6792 = 0.902665

⑤确定P值和作出推断结论本例H服从于 v=k-1=3-1=2的2分布,查x2界值表w X2o.0s2-5.99,今求得Hc-73.87>5.99,故P <0.05,按a=0.05水准拒绝H。认为三种类 型颈动脉炎眩晕患者的疗效不同或不全相同。 第四节 配伍组设计的秩和检验 (Friedman检验 配伍组设计(亦称随机区组设计)是配对设计 的扩展,若数据满足方差分析的条件,可采用前 授的两因素方差分析,若数据不满足方差分析 吉林大学远程教育学院
11 吉林大学远程教育学院 ⑤ 确定P值和作出推断结论 本例Hc服从于 ν =k-1=3-1=2的χ 2分布,查χ 2界值表χ 2 α(ν)= χ 2 0.05(2)=5.99,今求得Hc=73.87>5.99,故P <0.05,按α=0.05水准拒绝H0。认为三种类 型颈动脉炎眩晕患者的疗效不同或不全相同。 第四节 配伍组设计的秩和检验 (Friedman检验) 配伍组设计(亦称随机区组设计)是配对设计 的扩展,若数据满足方差分析的条件,可采用前 授的两因素方差分析,若数据不满足方差分析