
第十二章 非参数统计 前面讲述的统计推断方法,通常要求样本来自的 总体分布类型是已知的,在此种假设基础上,对总 体参数进行估计或检验,称为参数统计(parametric statistics)。在实际工作中,有许多资料不满足参 数统计的要求,如总体分布类型不清、总体分布偏 态且无法通过数据转换使其符合参数统计的要求 等,此时参数统计已不适用,需用一种不依赖于 总体分布类型,也不对总体参数进行统计推断的 统计分析方法,称为非参数统计(nonparametric statistics)。 吉林大学远程教育学院
2 吉林大学远程教育学院 第十二章 非参数统计 前面讲述的统计推断方法,通常要求样本来自的 总体分布类型是已知的,在此种假设基础上,对总 体参数进行估计或检验,称为参数统计(parametric statistics)。在实际工作中,有许多资料不满足参 数统计的要求,如总体分布类型不清、总体分布偏 态且无法通过数据转换使其符合参数 统计的要求 等,此时参数统计已不适用,需用一 种不依赖于 总体分布类型,也不对总体参数进行 统计推断的 统计分析方法,称为非参数统计(nonparametric statistics)

非参数统计的主要优点是不受总体分布类型的 限制,适用范围广。非参数统计方法对数据的要 求也不高。不论研究的是何种类型的数据,包括 那些难以精确测定、只能以严重程度、优劣等级 次序先后等表示的数据;或有的数据出现不确 定数值,如“>20岁”或”<80岁”等,均可用 非参数统计。 非参数统计的不足之处是,当符合参数统计的 资料,若用非参数统计处理,因未能充分利用资 料提供的信息,检验效率常低于参数统计,犯Ⅱ 型错误的概率增大。 吉林大学远程散育学院
3 吉林大学远程教育学院 非参数统计的主要优点是不受总体分布类型的 限制,适用范围广。非参数统计方法对数据的 要 求也不高。不论研究的是何种类型的数据,包 括 那些难以精确测定、只能以严重程度、优劣等 级 、次序先后等表示的数据;或有的数据出现不 确 定数值,如“>20岁”或“<80岁”等,均可用 非 参数统计。 非参数统计的不足之处是,当符合参数统计 的 资料,若用非参数统计处理,因未能充分利用 资 料提供的信息,检验效率常低于参数统计,犯 II 型错误的概率增大

在实际应用中,符合参数统计条件的资料,要首 选参数统计的方法。当参数统计的应用条件得不 到满足时,应选用非参数统计。 非参数统计方法很多,本讲选用其中检验效率较 高的、理论体系比较完整的、常用的秩和检验( rank sum test)。 第一节 配对设计的符号秩和检验 (Wilc0xon配对法) 吉林大学远程教育学院
4 吉林大学远程教育学院 在实际应用中,符合参数统计条件的资料,要首 选参数统计的方法。当参数统计的应用条件 得不 到满足时,应选用非参数统计。 非参数统计方法很多,本讲选用其中检验效率较 高的、理论体系比较完整的、常用的秩和检 验( rank sum test)。 第一节 配对设计的符号秩和检验 (Wilcoxon 配对法)

对于配对设计的定量资料,Vilcoxon配对法通 过检验配对资料的差值是否来自中位数为零的总 体作出推断结论。 一、基本原理和方法 例12.1 为研究出生前后的李生兄弟间智力是否存在差异,选 用12对李生兄弟对其智力进行了测试,结果见下表12-1。 本研究属于异源配对中两观察者分别施加同种 处理,看观察者的个体差异对实验指标(即智力 得分)的影响。 吉林大学远程教育学院
5 吉林大学远程教育学院 对于配对设计的定量资料,Wilcoxon 配对法通 过检验配对资料的差值是否来自中位数为零的总 体作出推断结论。 一、基本原理和方法 例12.1 为研究出生前后的孪生兄弟间智力是否存在差异,选 用12对孪生兄弟对其智力进行了测试,结果见下表12-1。 本研究属于异源配对中两观察者分别施加同种 处理,看观察者的个体差异对实验指标(即智力 得分)的影响
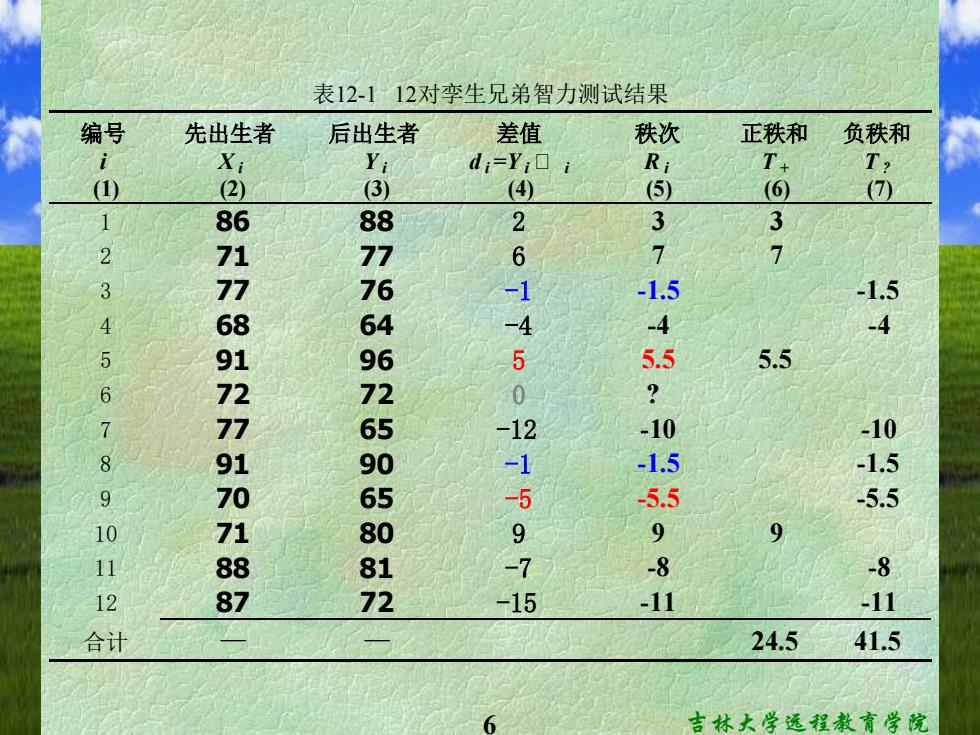
表12-112对孪生兄弟智力测试结果 编号 先出生者 后出生者 差值 秩次 正秩和 负秩和 Yi di=YiO i Ri T+ T> () (2) (3) (4) (⑤) (6) (7 1 86 88 2 3 2 77 6 1 7 3 76 -1 -1.5 -1.5 4 64 -4 -4 -4 5 9 5 5.5 5.5 6 0 65 -10 8 17612710187 1 -1.5 9 -5 5.5 55 9 9 9 1 -7 -8 -8 72 -15 -11 -11 合计 24.5 41.5 6 吉林大学远程教育学院
6 吉林大学远程教育学院 编号 先出生者 后出生者 差值 秩次 正秩和 负秩和 i X i Y i d i =Y i 朮 i R i T + T ? (1) (2) (3) (4) (5) (6) (7) 1 86 88 2 3 3 2 71 77 6 7 7 3 77 76 -1 -1.5 -1.5 4 68 64 -4 -4 -4 5 91 96 5 5.5 5.5 6 72 72 0 ? 7 77 65 -12 -10 -10 8 91 90 -1 -1.5 -1.5 9 70 65 -5 -5.5 -5.5 10 71 80 9 9 9 11 88 81 -7 -8 -8 12 87 72 -15 -11 -11 合计 — — 24.5 41.5 表12-1 12对孪生兄弟智力测试结果

本检验的基本思想是:计算每对观察值差数的 绝对值,省略所有差数为零的对子,然后根据余 下的差数的绝对值的大小,由小到大排秩,遇有 相同者,取平均秩次;将所排的秩次标以原差数 的符号,分别求正秩和T,与负秩和T。 假设本例中孪生兄弟间智力无差别,即Ho:M。 =0(差值总体中位数等于零),T,与T.一般相差 不大;若相差较大,则拒绝Ho。通过统计学家制 作的相应T界值表,获得H成立与否的概率P值, 再根据检验水准作出推断结论。 吉林大学远程教育学院
7 吉林大学远程教育学院 本检验的基本思想是:计算每对观察值差数的 绝对值,省略所有差数为零的对子,然后根据余 下的差数的绝对值的大小,由小到大排秩,遇有 相同者,取平均秩次;将所排的秩次标以原差数 的符号,分别求正秩和T+与负秩和T-。 假设本例中孪生兄弟间智力无差别,即H0 : Md =0(差值总体中位数等于零),T+与T-一般相差 不大;若相差较大,则拒绝H0。通过统计学家制 作的相应T界值表,获得H0成立与否的概率P值, 再根据检验水准作出推断结论

本例的检验步骤如下: ①检验假设 H0:M。=0即孪生兄弟间得分差值的总体中位数等于0 H:Ma≠0 0u=0.05 ②求差值 dY Xi 见表12-1中的4。 ③编秩按差值的绝对值由小到大排秩,并依 差值的正负给秩次标正负号。差值为0者,不 参于排秩,同时对子数减1;差值相等,取平 均秩次。见表12-1中的⑤)。 吉林大学远程教育学院
8 吉林大学远程教育学院 H0 : Md =0 即孪生兄弟间得分差值的总体中位数等于0 H1 : Md ≠0 α= 0.05 本例的检验步骤如下: ① 检验假设 ② 求差值 di=Yi–Xi 见表12-1中的(4) 。 ③ 编秩 按差值的绝对值由小到大排秩,并依 差值的正负给秩次标正负号。差值为0者,不 参于排秩,同时对子数减1;差值相等,取平 均秩次。见表12-1中的(5)

④求秩和并确定检验统计量分别求正秩 和T,与负秩和T.。见表12-1中的⑥、。 任取T,或T作为检验统计量T。本例T,-T =24.5。 ⑤确定P值和作出推断结论当(对子数) ≤50时,查附表8T界值表(配对比较的符号秩和 检验用)Tam,为检验水准,n为对子数]。 若检验统计量T值在界值范围内则P>: T值在界值范围外,则P0.05。 吉林大学远程教育学院
9 吉林大学远程教育学院 ④ 求秩和并确定检验统计量 分别求正秩 和T+与负秩和T-。见表12-1中的(6)、(7)。 任取T+或T-作为检验统计量T。本例T+ = T =24.5。 ⑤ 确定P值和作出推断结论 当n(对子数) ≤50时,查附表8 T界值表(配对比较的符号秩和 检验用)[Tα(n),α为检验水准,n为对子数]。 若检验统计量T值在界值范围内,则P >α; T值在界值范围外,则P <α;T值等于界值; 则P =α。本例Tα(n)=T0.05(11)=10-56,而T =24.5在界值范围内,故P >0.05

则按a=0.05水准尚不能拒绝H,,认为 孪生兄弟间智力无统计学差异。 二、正态近似法 当对子数n>25,则T的分布已较好地近似以均 数为n(n+1/4,方差为nn+1(2n+1)/24的正态分布 ,可用检验。当相同的秩次不多时,可用下式计 算u值: T-n(n+1)/4-0.5 = 公式(12.1 Vn(n+1)(2n+1)/24 10 吉林大学远程教育学院
10 吉林大学远程教育学院 则按α=0.05水准尚不能拒绝H0,认为 孪生兄弟间智力无统计学差异。 当对子数n>25,则T的分布已较好地近似以均 数为n(n+1)/4,方差为n(n+1)(2n+1)/24的正态分布 ,可用u检验。当相同的秩次不多时,可用下式计 算u值: 二、正态近似法 ( 1)(2 1)/ 24 ( 1)/ 4 0.5 + + − + − = n n n T n n u 公式(12.1)

式中0.5为连续性校正系数。因为T分布为离散型,而u 分布为连续型,故需校正。 当相同的秩次较多时,用公式(12.1)求得的u值偏 小,应改用下式校正。 T-n(n+1)/4-0.5 uc 公式(12.2) V(n+102n+)-0.5∑G-t】124 式中t为第(j=1,2,3,)个相同差值个数。 假定差值中有2个1,3个5,4个3,则=2,2= 3642G-7,)=2-2+6-3+4-4到=90。 吉林大学远程教育学院
11 吉林大学远程教育学院 当相同的秩次较多时,用公式(12.1)求得的u值偏 小,应改用下式校正。 式中0.5 为连续性校正系数。因为T分布为离散型,而u 分布为连续型,故需校正。 + + − − − + − = [ ( 1)(2 1) 0.5 ( )]/ 24 ( 1)/ 4 0.5 3 j j c n n n t t T n n u 公式(12.2) 式中t j为第j ( j = 1, 2, 3, …)个相同差值个数。 假定差值中有2个1,3个5,4个3,则t1=2, t2 = 3, t3=4, ( ) (2 3 2) (3 3 3) (4 3 4) 90。 3 3 − = − + − + − = j j j t t