
第三节 离牧趋势指标 本章第一节讲授的频数分布有集中趋势和离散 趋势两个特征,说明描述资料的全面变化规律需 把二者结合起来。通过下例可说明这个问题。 例10.8现有3组健康女大学生的口腔温度测得值如下,试分析 其集中趋势和离散趋势。 1组36.836.937.037.137.2 X1=37.0 2组36.536.937.037.137.5 X,=37.0 3组36.536.737.037.337.5 X3=37.0 吉林大学远程教有学院
2 吉林大学远程教育学院 第三节 离散趋势指标 本章第一节讲授的频数分布有集中趋势和离散 趋势两个特征,说明描述资料的全面变化规律需 把二者结合起来。通过下例可说明这个问题。 例10.8 现有3组健康女大学生的口腔温度测得值如下,试分析 其集中趋势和离散趋势。 1组 36.8 36.9 37.0 37.1 37.2 2组 36.5 36.9 37.0 37.1 37.5 3组 36.5 36.7 37.0 37.3 37.5 X1 = 37.0 X2 = 37.0 37.0 X3 =
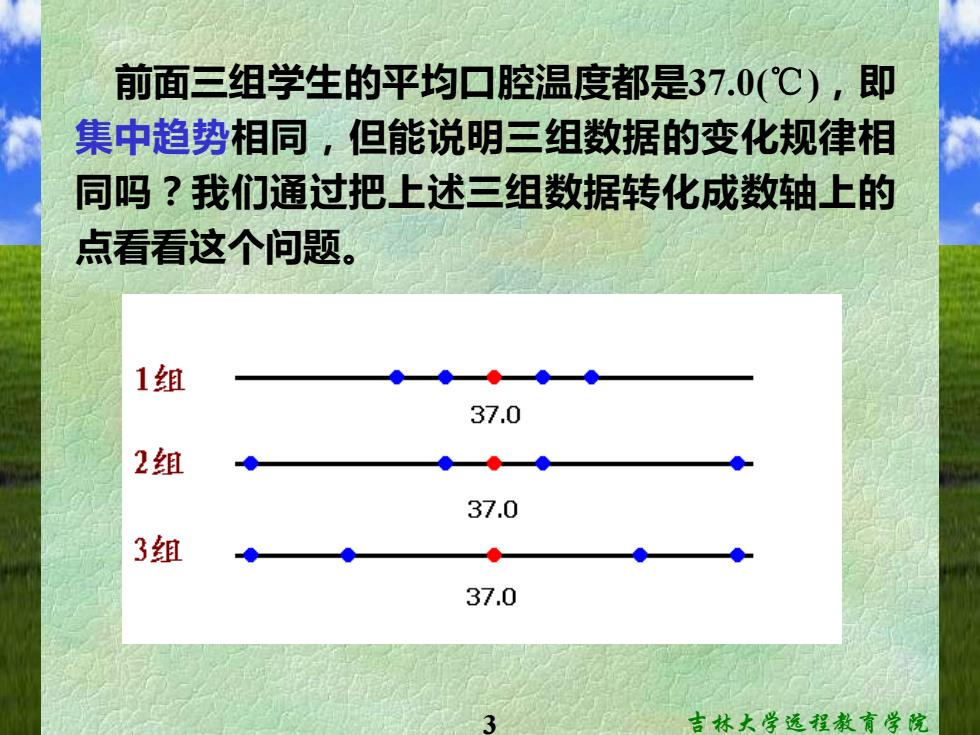
前面三组学生的平均口腔温度都是37.0(℃),即 集中趋势相同,但能说明三组数据的变化规律相 同吗?我们通过把上述三组数据转化成数轴上的 点看看这个问题。 1组 37.0 2组 ◆◆ 37.0 3组 37.0 3 吉林大学远程教育学院
3 吉林大学远程教育学院 前面三组学生的平均口腔温度都是37.0(℃),即 集中趋势相同,但能说明三组数据的变化规律相 同吗?我们通过把上述三组数据转化成数轴上的 点看看这个问题

显然三组学生的口腔温度值参差不齐的程度都 各不相同。第1组数值较为集中,第2、3组数值较 为发散。说明三组数据的离散趋势是不相同的。 统计学中常用描述变量值的离散趋势(亦称变 异程度)的指标有:极差、四分位数间距、方差、 标准差和变异系数。 一、极差 极差亦称全距,用R表示。极差是所有变量 吉林大学远程教育学院
4 吉林大学远程教育学院 显然三组学生的口腔温度值参差不齐的程度都 各不相同。第1组数值较为集中,第2、3组数值较 为发散。说明三组数据的离散趋势是不相同的。 统计学中常用描述变量值的离散趋势(亦称变 异程度)的指标有:极差、四分位数间距、方差、 标准差和变异系数。 一、极差 极差亦称全距,用R表示。极差是所有变量

值中最大值与最小值之差,它反映了变量值的变 异范围大小。极差大变异程度大;极差小变异程 度小。 例10.8中,R1=37.2-36.8=0.4、R2=1.0、R3 1.0。说明第1组数据的离散趋势比第2、3组小。 极差计算简便,但粗略,不稳定。 例10.8中,R2=R3=1.0,并不能说明两组数据的 离散趋势一样。 极差易受极大或极小值的影响。 吉林大学远程教育学院
5 吉林大学远程教育学院 值中最大值与最小值之差,它反映了变量值的变 异范围大小。极差大变异程度大;极差小变异程 度小。 例10.8中,R1=37.2-36.8=0.4、R2=1.0、 R3= 1.0。说明第1组数据的离散趋势比第2、3组小。 极差计算简便,但粗略,不稳定。 例10.8中,R2=R3=1.0,并不能说明两组数据的 离散趋势一样。 极差易受极大或极小值的影响
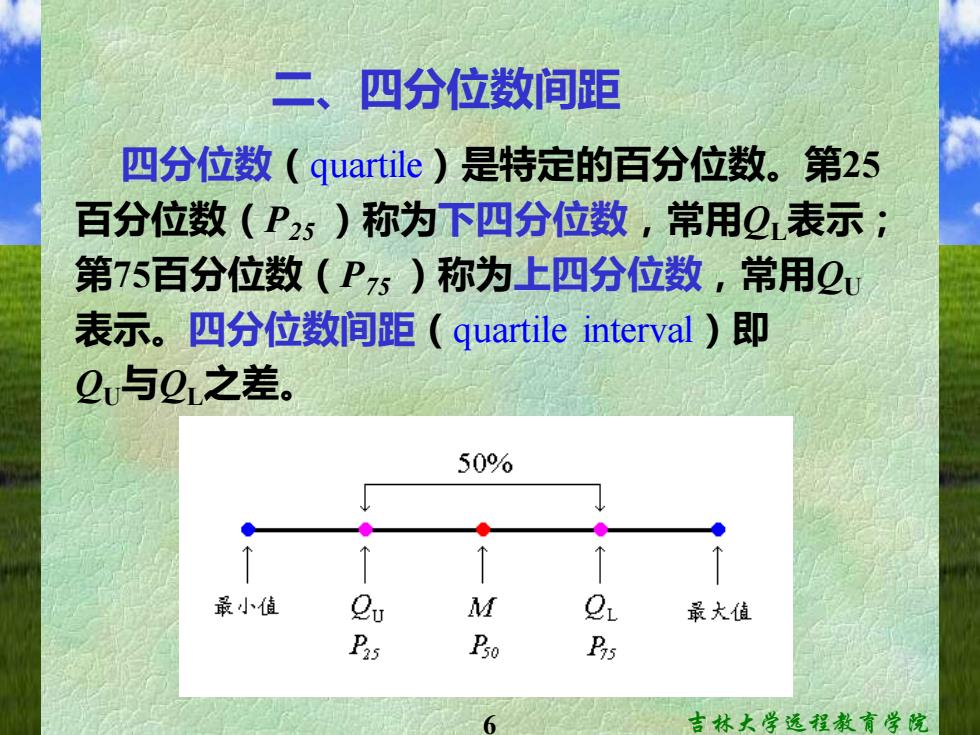
二、四分位数间距 四分位数(quartile)是特定的百分位数。第25 百分位数(P25)称为下四分位数,常用2表示: 第75百分位数(P5)称为上四分位数,常用Q 表示。四分位数间距(quartile interval)即 2与01之差。 50% 最小值 Cu M Cl 最大值 Bs P3o Bs 吉林大学远程教育学院
6 吉林大学远程教育学院 二、四分位数间距 四分位数(quartile)是特定的百分位数。第25 百分位数(P25 )称为下四分位数,常用QL表示; 第75百分位数(P75 )称为上四分位数,常用QU 表示。四分位数间距(quartile interval)即 QU与QL之差

四分位数间距适用于偏态分布资料,尤其是 有特大或特小值;分布末端无确切数值的资料。 例10.9求例10.7资料的四分位数间距。 在前面百分位数一节已求得P25=8.42,P75=19.05,则 四分位数间距为: 9-Q=19.05-8.42=10.63(小时) 四分位数间距虽比极差稳定,但仍未考虑所 有变量值的变异程度。 吉林大学远程教育学院
7 吉林大学远程教育学院 四分位数间距适用于偏态分布资料,尤其是 有特大或特小值;分布末端无确切数值的资料。 例10.9 求例10.7资料的四分位数间距。 在前面百分位数一节已求得P25 =8.42,P75 =19.05,则 四分位数间距为: − =19.05−8.42 =10.63(小时) QU QL 四分位数间距虽比极差稳定,但仍未考虑所 有变量值的变异程度

三、方差 方差(variance)是常用的变异指标。总体方 差用σ表示,样本方差用S2表示。总体方差往往 未知,常用样本方差来估计。 方差的计算公式为: g2-2(X-4)2 公式(10.10) N S2- (X-) 公式(10.11) n-1 8 吉林大学远程教育学院
8 吉林大学远程教育学院 三、方差 方差(variance)是常用的变异指标。总体方 差用σ 2表示,样本方差用S 2表示。总体方差往往 未知,常用样本方差来估计。 方差的计算公式为: 1 ( ) 2 2 − − = n X X S N X 2 2 ( ) − = 公式(10.10) 公式(10.11)

式中分子称为离均差平方和;n~I称为自由度(degree of freedom)。 四、标准差 标准差(standard deviation)是方差的平方根。 因方差使度量衡单位变成平方,故对方差开平方 根恢复原单位就得到标准差。总体标准差用σ表示, 样本标准差用S表示。计算公式为: 62N (X-02 公式10.12) 9 吉林大学远程教育学院
9 吉林大学远程教育学院 式中分子称为离均差平方和;n-1称为自由度(degree of freedom )。 四、标准差 标准差(standard deviation)是方差的平方根。 因方差使度量衡单位变成平方,故对方差开平方 根恢复原单位就得到标准差。总体标准差用σ表示, 样本标准差用S表示。计算公式为: N X 2 ( ) − = 公式(10.12)

5-1 (X-)2 公式(10.13) n-1 离均差平方和 (X常用或表示。其展开 式为: 2(X-X)3=x2-②X) n 把上述展开式代入公式10.13)则得到直接由原始 数据求标准差的公式: S=1 X2-(x)}/n 公式(10.14) n-1 10 吉林大学远程教有学院
10 吉林大学远程教育学院 1 ( ) 2 − − = n X X S 公式(10.13) 离均差平方和 常用SS或lxx表示。其展开 式为: 2 (X − X) n X X X X 2 2 2 ( ) ( ) − = − 把上述展开式代入公式(10.13)则得到直接由原始 数据求标准差的公式: ( ) 1 2 2 − − = n X X n S 公式(10.14)

式中 变量值平方的和; 烹量值和 的平方。 上式为直接法的计算公式,下式为加权法的: S= x2-(X)/n 公式(10.15) n-1 式中X是各组段的组中值,f是相应的频数。 例10.10求例10.8三组数据的格自标准差。 求第1组的S1: X2=36.82+36.92+37.02+37.12+37.22=6845.1 (X)2=(36.8+36.9+37.0+37.1+37.2)2=1852=34225 11 吉林大学远程教育学院
11 吉林大学远程教育学院 式中 是变量值平方的和; 是变量值和 的平方。 上式为直接法的计算公式,下式为加权法的: 2 X 2 (X ) ( ) 1 2 2 − − = n f X f X n S 公式(10.15) 式中X 是各组段的组中值,f 是相应的频数。 例10.10 求例10.8三组数据的各自标准差。 36.8 36.9 37.0 37.1 37.2 6845.1 2 2 2 2 2 2 X = + + + + = 求第1组的S1: ( ) (36.8 36.9 37.0 37.1 37.2) 185 34225 2 2 2 X = + + + + = =