
Designing a multivariate EWMA control chart Designing a Multivariate EWMA Control Chart SHARAD S.PRABHU SAS Institute,Cary,NC 27515 GEORGE C.RUNGER Arizona State University,Tempe,AZ 85287-5906 ove the detection AmultivariatentrRecommendations provied for the seon of of the scheme. Introduction proces (198).Pignatielo and Runge 1nCkson19 lootrol a univariate control charts on individual variables. process inean vector jndethecontrol h the charts have been used to improve the detection of of the process. rom targe d denote the knowu covarlance matrix of X:as E.The chi-squared chart plots nd Runger() T=X∑-1X age(MEWMA) Howeve because the analysi iations for designing these schemes has been lim 8Dm。 of the Techuical Staf in the Sta schemes that provides recommendations for 11000 oumal of Quality Technology 8 Vol.9.No.1.January 1997 Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. Designing a multivariate EWMA control chart Prabhu, Sharad S; Runger, George C Journal of Quality Technology; Jan 1997; 29, 1; ABI/INFORM Global pg. 8

DESIGNING A MULTIVARIATE EWMA CONTROL CHART 9 r and Prabbu(1gg7)p an it We prefer to plot the statistic NEWNA The select the parameters for the design of a MEWMA g=W:ll 4 aa dcabCarttha pace. Saccucci (1990). The Markov chain analysis pro distribution of can be the distribution ofn I-squared di state.and worst-state cases parameter is a function of the current state of the Markecan MEWMA Control Chart The univariate eWMA chart was introduced by Roberts(1959).Whe the MEWMA is a function o only through the noncentrality parameter,Runge W:=rX:+(1-r)W- where Wo =0 and 0H 3) n to achieve a specified in- and Prabhu (1997)). ARLWe the opotie ties.Assume that a Markov chain has s states corre- The performance of a MEWMA chart was shown by sponding be denoted as Pwheu the process mean is6.Let )/.By the transformation we can assume Vol.29.No.1.January 1997 Journal of Quality Technology Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission
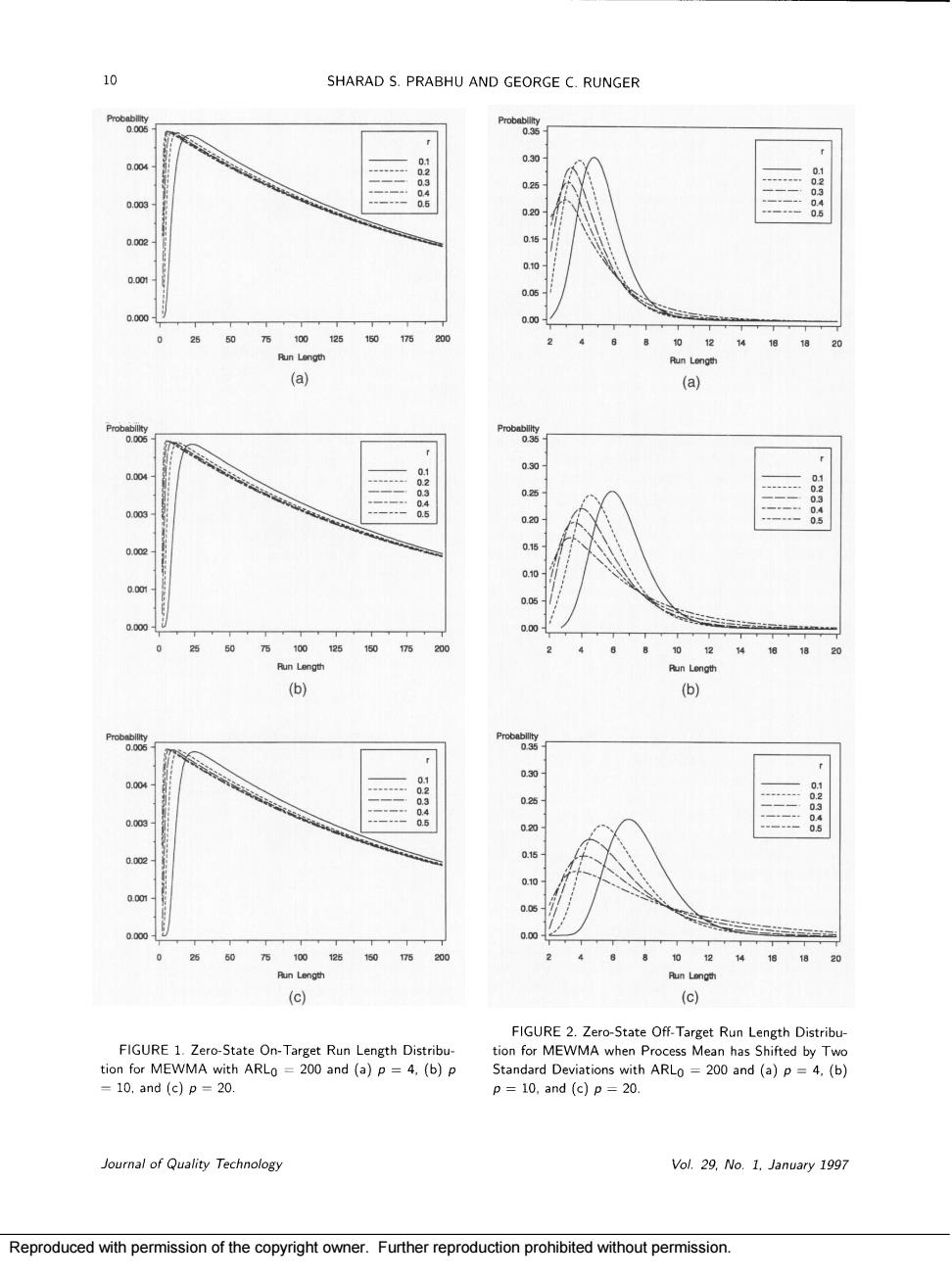
10 SHARAD S.PRABHU AND GEORGE C.RUNGER 0.25 。 (a) 0 20 b 2% (c) (c) FIGURE 2.Zero-State Off-Target Run Length Distribu tion for VMMA whe 55 with ARL o has and (a)p= =10.and(cp=20. p=10.and(c)p=20. Journal of Quality Technology Vol.29.No.1.January 1997 Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

DESIGNING A MULTIVARIATE EWMA CONTROL CHART TABLE 1.Zero-State Average Run Lengths for Multivariate EWMA Control Schemes 0.05 0.10 0.20 0.30 0.40 0.50 0.60 0.80 H 7.35 8.64 9.6 10.08 10.31 10.44 10.52 10.58 2 0.9 248 湖 H 11.22 12.73 3.87 14.34 14.5 04.7 4.8 199.9 D500 128 23 2.7 H= 14.60 16.27 17.51 18.01 18.26 18.39 18.45 18.54 6 200.11 200 199.8 0500 3.0g 24.07 462 24 80 2511 251 10 0500 27.82 30.03 31.59 32.19 32.48 32.63 32.7 32.79 15 05 200.08 20 28 6.16 380 343 oresponding to the starting the cha simulation al. E the s vector of all ones The arls of a contro ate chain divides the vertical axis into m+1 state scheme modeled as a Markov chain is adtehorizoaalarnio2 -I states Initially ARLs=b'(I-Ps)-11. (6) states. In some cases.a value of m -60 is used tale btaodincanca This s n in dibly e numbe he simpl he run length distribution of a two-dimensional Marko (Prabhu and Runger 19961.TC ults apply to Val.29,No.1,January 1997 Joural of Quality Technology Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission
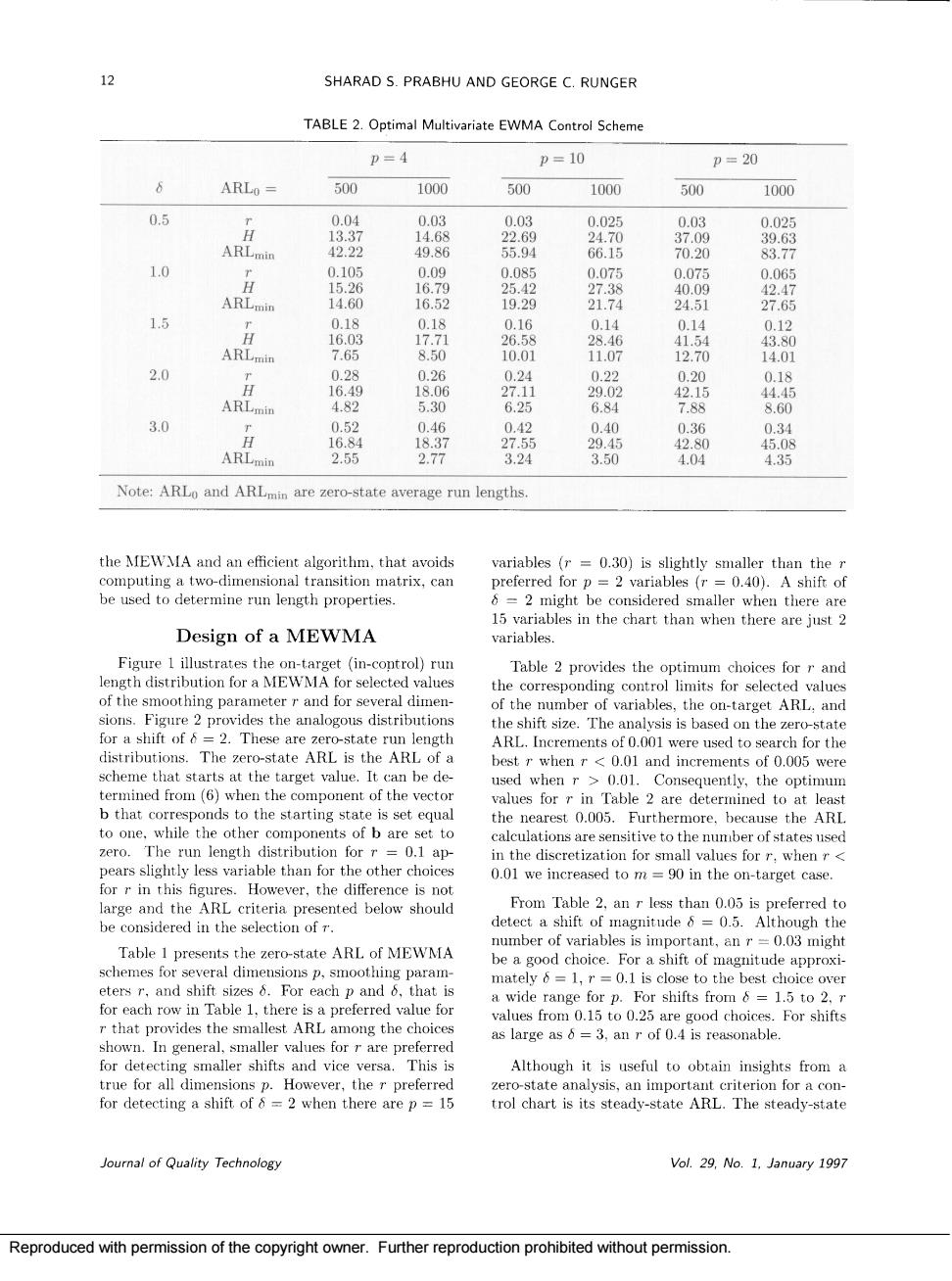
12 SHARAD S.PRABHU AND GEORGE C.RUNGER TABLE 2.Optimal Multivariate EWMA Controi Scheme P=4 p=10 p=20 ARLo= 500 500 1000 500 100 05 02 10 9 14.60 器 1.5 A 器 2.0 器 30 Note:ARLo and ARLmin are zero-state average run lengths. the MEWMA and an efficient algorithm.that avoids variables (r=0.30)is slightly smaller than the 0.40). Design of a MEWMA variables. ovidess the the corres and fo of the number of variables the on-target ARL,and =2.These are zer o-state run length edonthe7rotae The zero-state ARL is the ARLc used Consequently,the optimum ues for5 ed to calculations are sensitive to the umber of states used o e on-target case From Table 2,an r less than 0.05 is preferred to magnitude 6=0.5.Although the presents the zero-state ARL of MEWMA an 0.03 migh mately=,r=0.1 is close to the best choice over for each row in Table 1,there 0=1.5t0 onig the as large as6=3.an r of 0d is Although it is useful to obtain insights from a The steady-stat Journal of Quality Technology Vol.29,No.1.January 1997 Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission
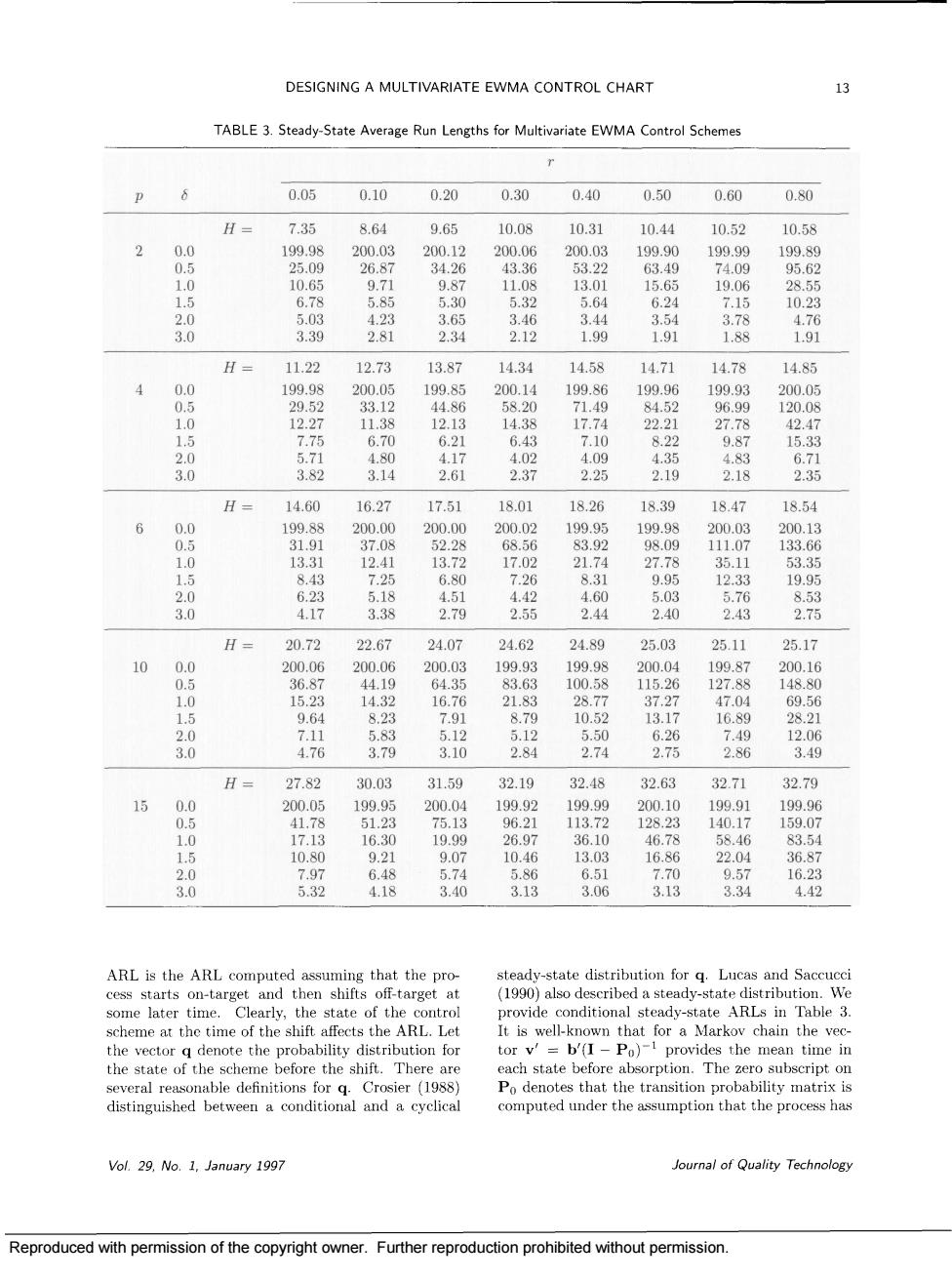
DESIGNING A MULTIVARIATE EWMA CONTROL CHART TABLE 3.Steady-State Average Run Lengths for Multivariate EWMA Control Schemes 0.05 0.10 0.20 0.30 0.40 0.50 0.60 0.80 HE 7.35 8.64 9.65 10.08 10.31 10.44 10.52 10.5 2900 2.81 2.34 H= 11.22 12.73 13.87 14.34 14.58 14.71 14.78 14.85 050 12 500 H 16.27 17.51 18.01 8.39 18.4 18.54 8:8 907 0152030 H= 20.72 22.67 24.0 24.62 2489 0511 )51 10 10.5 1689 H= 27.82 30.03 3159 32.19 32.48 32.63 32.71 32.7g 0505100 1 state dist ovide conditional steady-state ARLs in Table 3 scheme at the time of the shift affects the ARL.Let the the the mee state several reasonable definitions for g.Crosier (1988 distinguished between a conditional and a cyclical computed under the assumption that the process has Vol.9.No.1,January 1997 lournal of Quality Technology Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

14 SHARAD S.PRABHU AND GEORGE C RUNGER TABLE 4.Worst-State Average Run Lengths for Multivariate EWMA Control Schemes (H=15.1g元CL=±0.89 =±1.16) (H=40.s220 =士1.47 ZRaeARorH 3. 107.05 1424 220 14 088 464 115 557 二4 Note:ARLo=500,r=0.1,and the vertical location is zero for all cases. ieAaRwAoeo 4-VI Example Although.the matrix Po is the transition matrix etween all the transient state sults in Prabhu and Runger (1996).the large.two 0.7 88 0. 03 82 dimensional transition matrix can again be avoided 01 but slightly less than,the results in Table 1.When That is.thre and the EWM a state lations betweens the two sets are low to medium. the ARL i If the proce sonable choice for this size shift.Ther Now when the lewMA is in u state near a con 17.51 provides ARLo=200 and the (zer can be degra dodane 3 If the proce shifts tou(111 000)ther are considered in Table 4.By checking each state 6=('∑-1)/2=1.21.From Table1,r=0.1o 0.2 are reasonable choices.The performance can the les. e AR andr=0.1.In all cases in the table,the vertical is easily determined.If u is changed to u then changes to k6.for any constant k. location of the worst state is the zero axis.The hor Conclusions creases,the worst state is closer to-UCI This is pected becaus Our results indicate that good choices forrdepend e as d increa es.the probab ility tha in the cont state is nearer UCL.Table also provides the cor- teady-state analys not diferent responding zero-state ARLs for comparison.Similar than those for zero-state. The worst-state results Vol.29,No.1.January 1997 Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

DESIGNING A MULTIVARIATE EWMA CONTROL CHART 15 show the amount of degradation in arl that 1951 tained from the appropriate tables. References ns切 .S.E.(15)Double Integral Equation for 159.pp.530-549. 2Pp.351-365 Pm.20258 Cha Key Words:Avernge Run Length,Chi-Squared Con ContmlGhattHha tical Process Control. Vol.9.No.1,January 1997 Quality Technolog Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission