
第八章工序质量控制 第一节工序质量的受控状态 第二节工序能力指数 第三节工序质量控制图
第八章 工序质量控制 第一节 工序质量的受控状态 第二节 工序能力指数 第三节 工序质量控制图

第一节工序质量的受控状态 一、工序质量的两种状态 (一)受控状态(in control) (二)失控状态(out of control) 二、工序质量状态识别中的问题 生产制造过程是从设计质量到实物质量的实现过程,也是在 产品质量形成全过程中涉及职能部门最广及参与人员最多的 重要过程。 ● 生产制造过程控制的核心是工序质量控制,统计过程控制 (Statistical Process Control,简称SPC)是工序质量控制 的重要内容和方法。本章在第七章的基础上,对工序能力指 数、控制图等作较详细的介绍
第一节 工序质量的受控状态 一、工序质量的两种状态 (一)受控状态(in control) (二)失控状态(out of control) 二、工序质量状态识别中的问题 • 生产制造过程是从设计质量到实物质量的实现过程,也是在 产品质量形成全过程中涉及职能部门最广及参与人员最多的 重要过程。 • 生产制造过程控制的核心是工序质量控制,统计过程控制 (Statistical Process Control,简称SPC) 是工序质量控制 的重要内容和方法。本章在第七章的基础上,对工序能力指 数、控制图等作较详细的介绍

一、工序质量的两种状态 如工序质量特性值为X,其分布参数为μ和o,即X~N(4,o), 则工序质量的两种状态可以用μ和·的变化来判别。 (一)受控状态(in control) 工序质量处于受控状态时,质量特性值的分布特性不随时间而变 化,始终保持稳定且符合质量规格的要求。见图8-1。 在图8-1中,μ和o是排除了影响工序质量的系统性因素后,质 量特性值X或其统计量的数学期望和标准差,是工序质量控制的目 标。黑点表示随着时间的推移,X的观测值x(或X的统计量的观测 值,如样本平均值、样本中位数等)的散布情况。这些黑点依概率 散布在中心线()两侧,不应有任何系统性规律,且都介于上、 下控制限(UCL和LCL)之间
一、工序质量的两种状态 如工序质量特性值为X,其分布参数为μ和σ,即 , 则工序质量的两种状态可以用μ和σ的变化来判别。 (一)受控状态(in control) 工序质量处于受控状态时,质量特性值的分布特性不随时间而变 化,始终保持稳定且符合质量规格的要求。见图8-1。 在图8-1中,μ和σ是排除了影响工序质量的系统性因素后,质 量特性值X或其统计量的数学期望和标准差,是工序质量控制的目 标。黑点表示随着时间的推移,X的观测值x(或X的统计量的观测 值,如样本平均值、样本中位数等)的散布情况。这些黑点依概率 散布在中心线( )两侧,不应有任何系统性规律,且都介于上、 下控制限(UCL和LCL)之间。 ~ ( , ) 2 X N 0
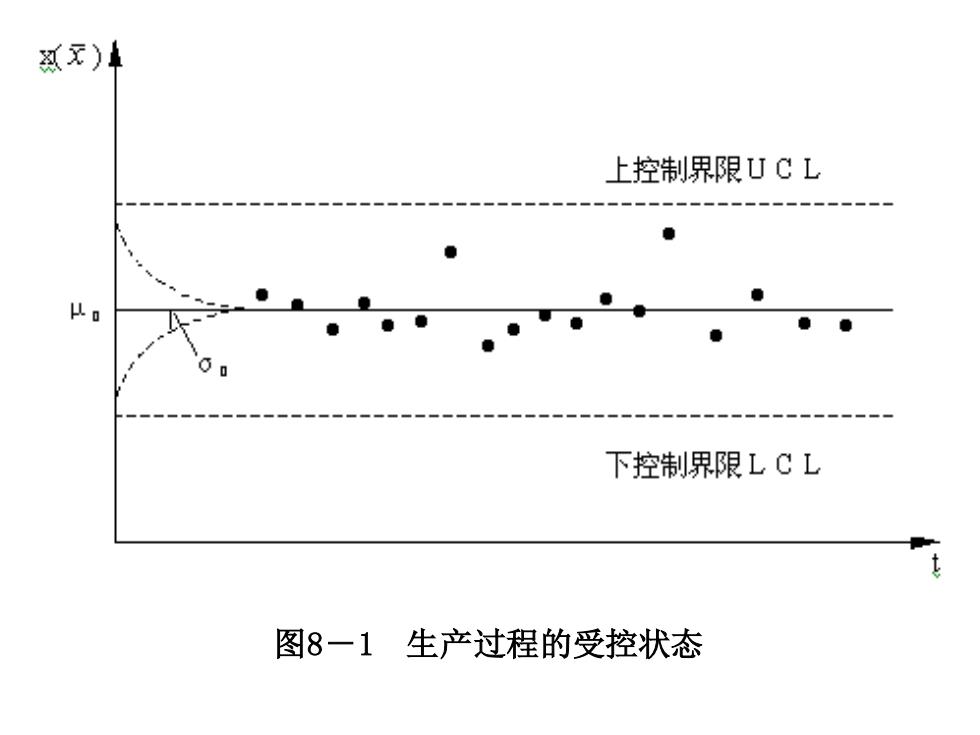
可元) 上控制界限UCL 下控制界限LCL 图8一1生产过程的受控状态
图8-1 生产过程的受控状态
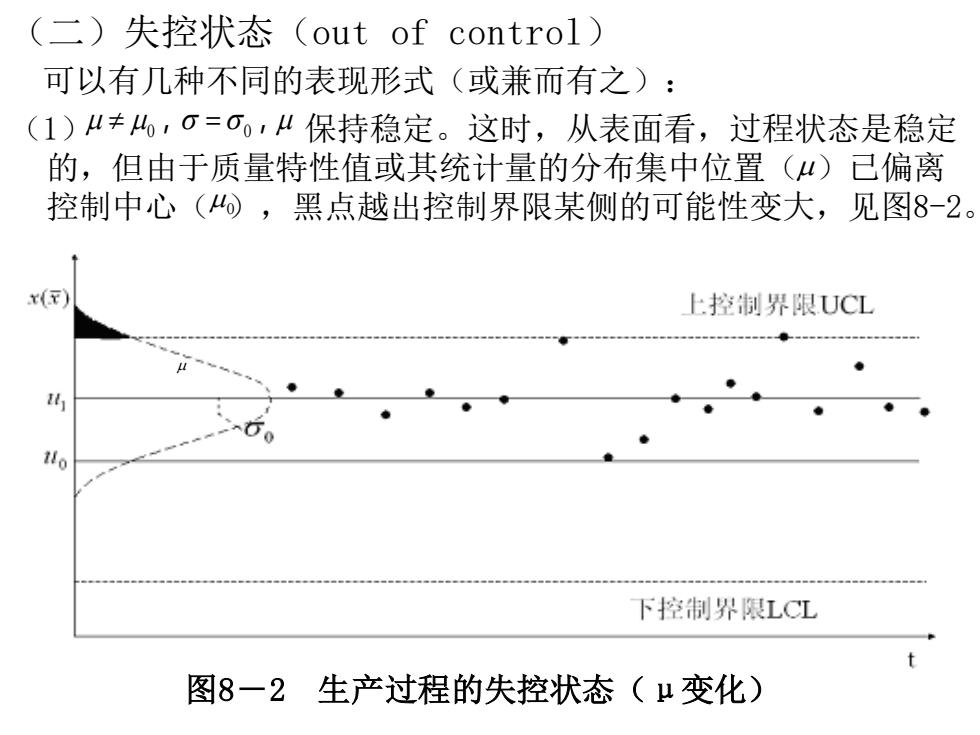
(二)失控状态(out of control) 可以有几种不同的表现形式(或兼而有之): (1)≠,=00,”保持稳定。这时,从表面看,过程状态是稳定 的,但由于质量特性值或其统计量的分布集中位置(4)已偏离 控制中心(),黑点越出控制界限某侧的可能性变大,见图8-2。 上控制界限UCL 1lo 下控制界限LCL 图8一2生产过程的失控状态(μ变化)
(二)失控状态(out of control) 可以有几种不同的表现形式(或兼而有之): (1) 保持稳定。这时,从表面看,过程状态是稳定 的,但由于质量特性值或其统计量的分布集中位置( )已偏离 控制中心( ),黑点越出控制界限某侧的可能性变大,见图8-2。 0, = 0, 0 图8-2 生产过程的失控状态(μ变化)
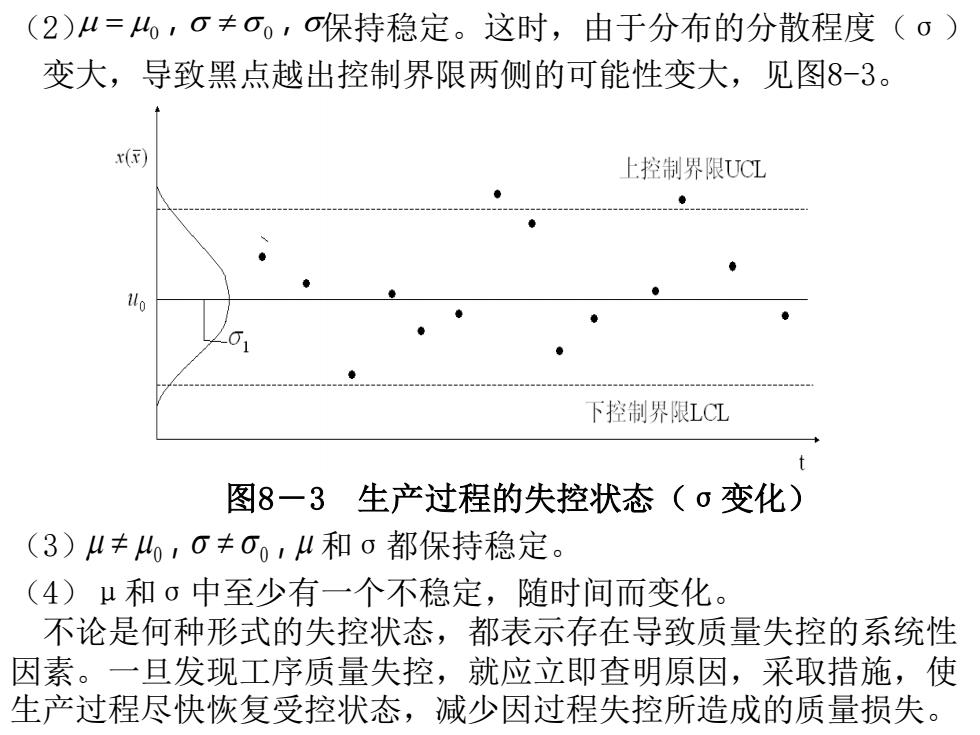
(2)4=4,O≠O,保持稳定。这时,由于分布的分散程度(0) 变大,导致黑点越出控制界限两侧的可能性变大,见图8-3。 () 上控制界限UCL 下控制界限LCL 图8一3生产过程的失控状态(σ变化) (3)1≠4,0≠00,4和0都保持稳定。 (4)μ和o中至少有一个不稳定,随时间而变化。 不论是何种形式的失控状态,都表示存在导致质量失控的系统性 因素。一旦发现工序质量失控,就应立即查明原因,采取措施,使 生产过程尽快恢复受控状态,减少因过程失控所造成的质量损失
(2) 保持稳定。这时,由于分布的分散程度(σ) 变大,导致黑点越出控制界限两侧的可能性变大,见图8-3。 图8-3 生产过程的失控状态(σ变化) (3) 和σ都保持稳定。 (4)μ和σ中至少有一个不稳定,随时间而变化。 不论是何种形式的失控状态,都表示存在导致质量失控的系统性 因素。一旦发现工序质量失控,就应立即查明原因,采取措施,使 生产过程尽快恢复受控状态,减少因过程失控所造成的质量损失。 = 0, 0, 0, 0,
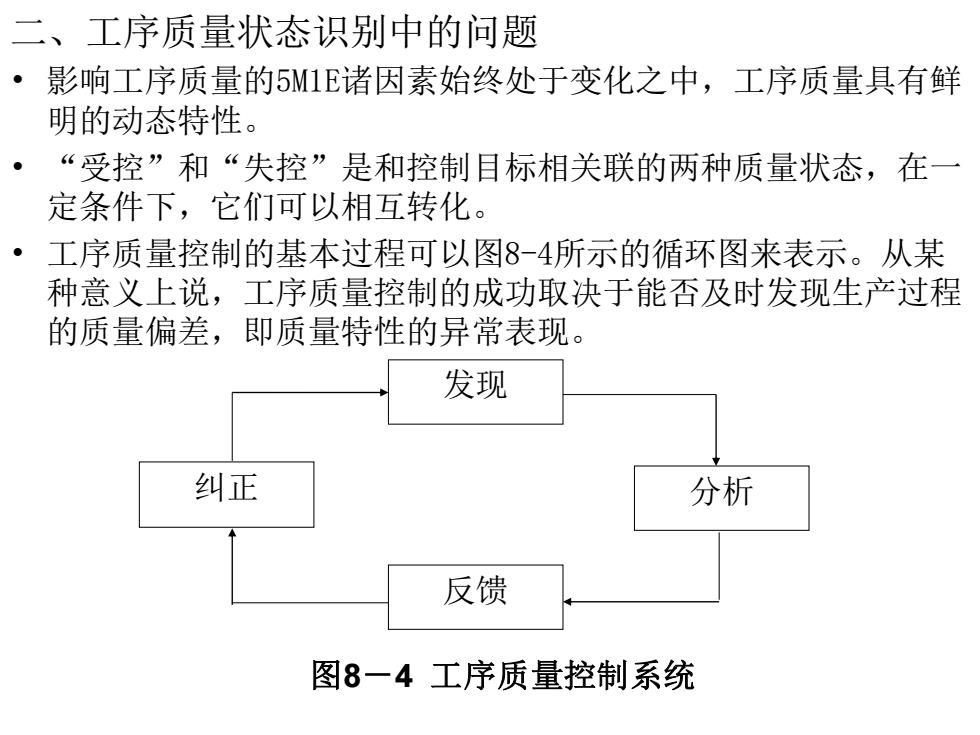
二、工序质量状态识别中的问题 ·影响工序质量的5M1E诸因素始终处于变化之中,工序质量具有鲜 明的动态特性。 ·“受控”和“失控”是和控制目标相关联的两种质量状态,在一 定条件下,它们可以相互转化。 ● 工序质量控制的基本过程可以图8-4所示的循环图来表示。从某 种意义上说,工序质量控制的成功取决于能否及时发现生产过程 的质量偏差,即质量特性的异常表现。 发现 纠正 分析 反馈 图8一4工序质量控制系统
二、工序质量状态识别中的问题 • 影响工序质量的5M1E诸因素始终处于变化之中,工序质量具有鲜 明的动态特性。 • “受控”和“失控”是和控制目标相关联的两种质量状态,在一 定条件下,它们可以相互转化。 • 工序质量控制的基本过程可以图8-4所示的循环图来表示。从某 种意义上说,工序质量控制的成功取决于能否及时发现生产过程 的质量偏差,即质量特性的异常表现。 发现 分析 反馈 纠正 图8-4 工序质量控制系统

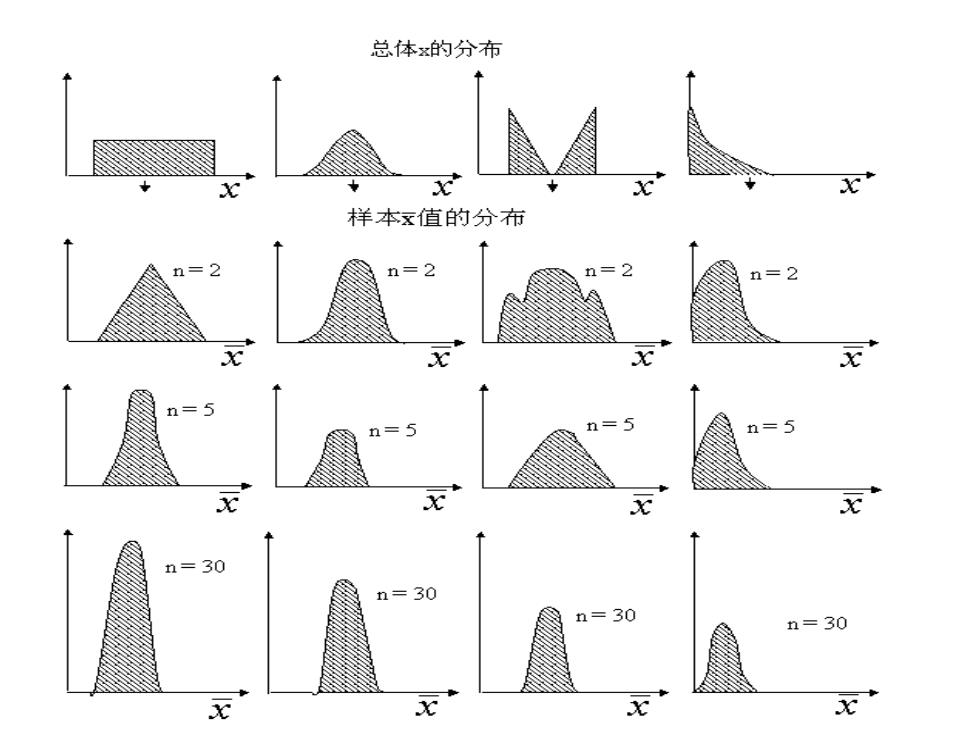
生产过程中工序质量异常波动的发现及原因的分析往往需要借助 数理统计中的统计推断方法。 ·对于各式各样的质量总体,经常可以用正态分布随机变量来描述 或近似描述,见图8-5所示。正态分布是统计推断中最广泛使用 的分布形式。在没有特殊条件的场合,总是假设所涉及的总体为 正态分布随机变量。 ·总体分布的数字特征,最常用的是总体数学期望μ和标准差σ (对于正态总体,其分布已被这两个参数唯一确定)。 总体数学期望μ常用样本平均值x来估计。样本平均值X是总体 数学期望H的无偏估计,即EX=μ。样本平均值X~“),计 算并不复杂。为了适应现场质量控制的要求,有时也用样本中位 数X来估计。X也是μ的无偏估计量,但计算更方便。 总体标准差o可用样本标准差s来估计,也可用样本极差R或R序 列的平均值R来估计。两者都是·的无偏估法秀但极差的计算要 容易得多。实际应用中,0的估计值。=元,其中是和 样本容量n有关的参数,可查表8-1
• 生产过程中工序质量异常波动的发现及原因的分析往往需要借助 数理统计中的统计推断方法。 • 对于各式各样的质量总体,经常可以用正态分布随机变量来描述 或近似描述,见图8-5所示。正态分布是统计推断中最广泛使用 的分布形式。在没有特殊条件的场合,总是假设所涉及的总体为 正态分布随机变量。 • 总体分布的数字特征,最常用的是总体数学期望μ和标准差σ (对于正态总体,其分布已被这两个参数唯一确定)。 • 总体数学期望μ常用样本平均值 来估计。样本平均值 是总体 数学期望μ的无偏估计,即 =μ。样本平均值 ~ ,计 算并不复杂。为了适应现场质量控制的要求,有时也用样本中位 数 来估计。 也是μ的无偏估计量,但计算更方便。 • 总体标准差σ可用样本标准差s来估计,也可用样本极差R或R序 列的平均值 来估计。两者都是σ的无偏估计,但极差的计算要 容易得多。实际应用中,σ的估计值 ,其中 是和 样本容量n有关的参数,可查表8-1。 − X − X − X − E X ( ) 2 n N , ~ X ~ X − R 2 ^ d R − = 2 d
总体x的分布 样本x值的分布 2 =2 n=5 =5 n=5 30 n =30 n=30 n=30
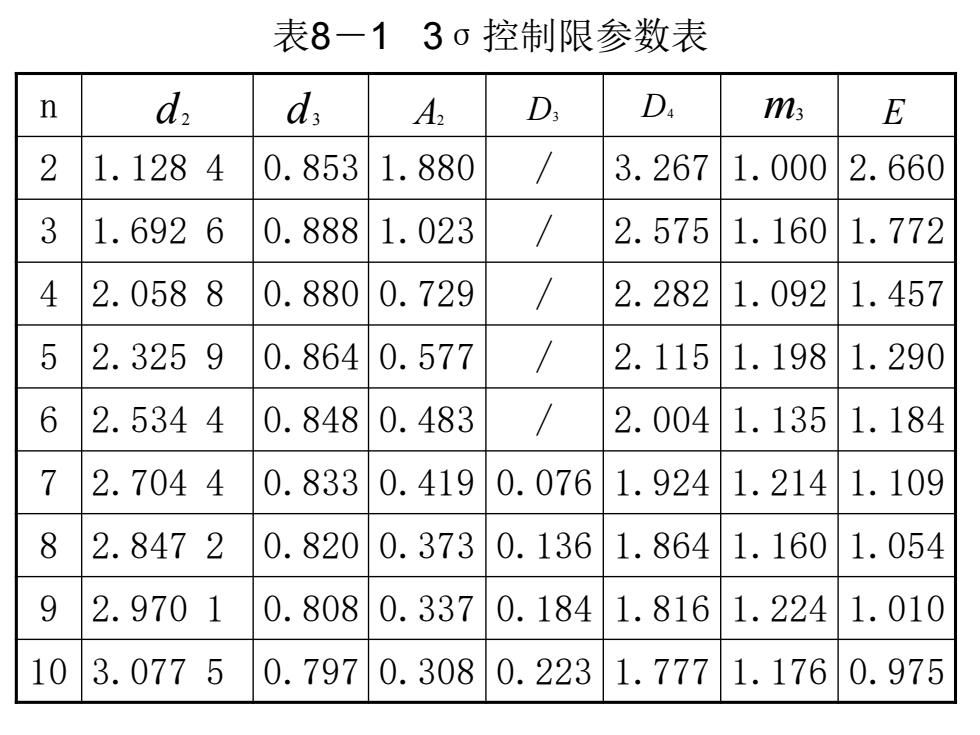
表8一13σ控制限参数表 n d d; A D D. m: E 2 1.1284 0.853 1.880 3.267 1.000 2.660 3 1.6926 0.888 1.023 2.575 1.160 1.772 4 2. 0588 0.880 0.729 2.282 1.092 1.457 5 2.3259 0.864 0.577 2.115 1.198 1.290 6 2.5344 0.848 0.483 2.004 1.135 1.184 7 2.7044 0.833 0.419 0.076 1.924 1.214 1.109 8 2.8472 0.820 0.373 0.136 1.864 1.160 1.054 9 2.9701 0.808 0.337 0.184 1.816 1.224 1.010 10 3.0775 0.797 0.308 0.223 1.777 1.176 0.975
表8-1 3σ控制限参数表 n 2 1.128 4 0.853 1.880 / 3.267 1.000 2.660 3 1.692 6 0.888 1.023 / 2.575 1.160 1.772 4 2.058 8 0.880 0.729 / 2.282 1.092 1.457 5 2.325 9 0.864 0.577 / 2.115 1.198 1.290 6 2.534 4 0.848 0.483 / 2.004 1.135 1.184 7 2.704 4 0.833 0.419 0.076 1.924 1.214 1.109 8 2.847 2 0.820 0.373 0.136 1.864 1.160 1.054 9 2.970 1 0.808 0.337 0.184 1.816 1.224 1.010 10 3.077 5 0.797 0.308 0.223 1.777 1.176 0.975 d2 d3 A2 D3 D4 m3 E