
ogy:Jan 1997 29 1 AbUINFORM Global Optimal Response Surface Designs in the Presence of Dispersion Effects DARCY P.MAYS Virginia Commonwealth University,Richmond,VA 23284-2014 STEPHEN M.EASTER Randolph-Macon College,Ashland.VA 23005-5505 Standard response surface des e ial d optimal fofirst-or or in ction model,and balanced thre evel factorial des d-ord ever,in many situations the andlevelofdispersiog esign when d with a first-order or in recommendations are made as to what types of designs are preferred in different heterogeneous variance Introduction T tion to a detailed list of references to recent work thecopinloperatiangconditions.Ttisetrendofat aed Taguchi.who incorporated the scientists. berg (and MeCullagh and Pregibon (17)in into a testing problem sion effects,and the use of t eAitkin (1987)and Davidian and Carroll ( r (1986)con rd the ctor desg which are applicabe to many man- ufacturing and scientific processes.However,with Vol.29.No.1.January 1997 Journai of Quality Technology Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. Optimal response surface designs in the presence of dispersion effects Mays, Darcy P; Easter, Stephen M Journal of Quality Technology; Jan 1997; 29, 1; ABI/INFORM Global pg. 59

DARCY P.MAYS AND STEPHEN M.EASTER only a few design or process variables,replication of over the design locations to which runs can actually be allocated. ically.one shoule eneous variance structure.to cates The results that follow involve determining the designs that could be use optimal distribution of design points for a given het when dispersion effects exist.The remainder of the paper The mean models used in the ture and the degree of the variability.One problem timate these models are described.Then the vari mary of the y; process that an "educated stimate of the varianc ommendation s as to which designs should be used in structurecanbr certain situations. be estimated using either some preliminary data or Models and Designs The analysis presented as The experiment consists of N runs,which are allo estimate of the variance structure through previou ferent mean models are considered: ary to experiment a first order model- h=%+E11+2x21+4 Experimental designs are often evaluated with re adtstmationofparametens a partial second-order or interaction model =30+31x14+32x2+12x12+6:(2) oaKfdai2o91od mat design a second-order model: the 斯=风+1+22:+31212 alized variance of the regresio +31x1+32x2,+, (3) the design matrix and Wre the ji ar nting a weight or sion parameters,and the are random errors or e is kno own as integrated variance or I-optimality locations to which the be located. models,such as the fr orde two-level factorial des pre gion ()and N to be the total number of runs the effect inclding the interaction term (Box an in the experiment,the /-optimal design minimizes Draper(1987).H three-leve actorial c Ixw-ix)x that the different variance structures that are consid. trnce (XW-x)xx'dx ered can be implemented.The second-order model the thr In the analysis that follows the evaluation of this in natural choice in this case.It is important to note tegrated variance function is made by averaging only that a three-level factorial structure is used,but tha oual of Qualit Technolo) Vol.29.No.I.January 1997 Reproduced with permission of the copyright owner.Further repr du ction pro hibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

OPTIMAL RESPONSE SURFACE DESIGNS IN THE PRESENCE OF DISPERSION EFFECTS 61 it is not necessary for the optimal design to require the variances at the low and middle levels of the vari- runs at all nine design locations. In addition to requiring three levels of each vari- g the varia structure type for each variable,are linear-linear inear-quadra at its low level,a value of o when the variable is at andatqusdhai vae ofI when the variable nverse quadratic sidered for eacl complete variance structure.Half of the cases involve eao大区hogon n which a me for each variable ance ratio but are。co parameters Th our cases conside d include ca s in which th Variance Structures as 1:1.1:4 and 1:2.1:8.Fortunately.the general con heariance ons depend on the size of the variance ratios,no rogeneous variance patter u in th of onof th hetero ussion,only six variance ratio cases are presented for alled"variance structure types",and the degrees of each variance structure simplest involves homo heterogeneity,callec ratios follows is a th based on ariable Small to moderate degre of dispersio models specified in (1).(2).and (3) 1:5.15 (0 by varianc ratios rsion cat ed,and th sented which fall within this moderate disp egory include 1:4,1:4:1:2.13:and 1:1,1:4).Severe by stating the appropriate variance structure type rati for each variable. 6.8ad22 The individ of the l riances are d but not presented include 1:6,1:6:1:8,1:8:and 1:2. to the highest variane ×2.denoted 1:8 1:V.The values of V and their interpretations are The variances that result from the specification presented shortly nce ratio t One variance structure type is a"linear"varianc and different variance ratios.This standardization (V)/2.and the high level of the variable hasa efactorandceat that are all positive and which sum to nine ariance of V Us- ng a three-lev variance struc MM type is a"quadratic variance structure,which has in the design region ble being os the low and high leve VLH VMH VHH VLM VMM VHM at the VLL VML -VHL ing at the middle level of the variable.Finally cubic"variance structures are considered,in which As an example,consider the case with variance Vol.29.No.1.January 1997 Joura!of Quality Technology Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

62 DARCY P.MAYS AND STEPHEN M.EASTER ratios 1:3 and 1:3 and complete variance structure design center.This creates three different levels for linear-cubic.The standardized variances for this case would be 0.9- 1.8-2.7 io the D-optimal de 0.3-0.6-0.9 this 0.3-0.6-09 optimal design is an unbalanced design,allocating In terms o 5,a d thre the variances at the high levels (VHL.VHM.and rial location:and hence is not appealing for practical use). at the ective low and middle an the standard designs involves calculating relative ef empt Thetandadodrianesthatresutorachofthe obtained fom the primary author. () Results wher ters in the mode The experiments being analyzed allow a total of mize 1=rae[xw-x/人xx ratio cases described the allocations of the 16 proces the the standard desig is co optimal d a-( In either case relative efficiencies at or near 100%in dicate that the standard design performs well,whil Once the optimal designs are determined,they are timal designs are significantly better. ction model in ()replicated and /-efficiencies of the standard design relative to fac optimal designs.The following subsections pro runs to ide indiv the standard design However.for the second-order ariance structure case model in (3)that contains six parameters, the Linear-Linear sign mus dor model.the standard design is For this variance structure the smallest variance balanced design that allocates one rn to each ccurs at(-1,-1)and the largest variance occurs a odel Journal of Quality Technology Vol.29.No.1.January 1997 Reproduced with permission of the copyright owner Further reproduction prohibited without permissior
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

OPTIMAL RESPONSE SURFACE DESIGNS IN THE PRESENCE OF DISPERSION EFFECTS 6 the D-optimal designs use the three factorial loca- ance ratios increase.although at a slow rate.and the standard design is remarkably efficient (in term suse the tim The interaction model requires at least four dis signs for the m ocation D-and ficiencies of the standard design decrease as the vari- cations. of larges mallest variance.Hence the f-efficiency of the stan the f-optimal designs First-Order Model so again the I-optimal designs are nearly invariant to the magnitude of the dispersion effects. For the second-order model both the D.and I optimal designs require runs at the factorial loca Efficiency100.0097.3291.2085.1082.4379.41 sandaditionmlkathee ocations with the quire runs in the design center.The D-optimal de signs for the mag designs Efficieney 100.0097.8591.9384.81772568.62 I-optimal designs are more invariant to the magni- tude of the dispersion effects,and the InteractionModel fectThe D-ecnc mplving that Do the standard design can be improved upon,particu- larly for severe dispersion effects Efficiency 100.00100.00100.00100.00100.00100.00 Linear-Quadratic t variance located in the design center.Facto E伍ciency c(1)and (1 the 100.0094.8187.50773169.8459.17 the Second-Order Model first-order model,the optimal designs now require uns at all four fact l de timal designs with more runs at the locations of large variance.The Efficiency 85.0682.5379.0874.5871.6067.61 ign is highly efficient 18 For the interactio model.the standard desig Efficiency100.0098.2197.0294.6691.7486.52 optimal designs place runs at all four factorial loca tions.again favoring the locations of large variance. Vol.29.No.1.January 199 Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

64 DARCY P.MAYS AND STEPHEN M.EASTER quantities,while the I-optimal designs require more the uns at (-1,0),the edge location with the second the dispersion effects.However,the efficiency of the First-Order Model tandarddcsigasteducedparticuaryinterms D the experimenter is advised to consider a design other than the standard design. Efficiency 10.0099.4898.2497.0696.7395.8 Ouadratic-ouadratic In this the fou rial locati each ha I-8en the same variance,which is the smallest variance in the design region.The four edge locations also have Efficiency 10.0099.2896.6192.6891.3483.31 arger)variance,.and the】 it is logical that for al eves of dispersion effects the Interaction Model standardd esign is both and for severe dispersion effects the I-optimal de the runs from the design center Efficiency 100.00100.00100.0010.00100.00100.00 Once one goe from mild to severe dispersion effects ects.For any the design center,and are also fairly invariant to the Efficiency 100.0097.7893.3388.8985.7176.92 nemnteofthetpenaic Therefore,the Second-Order Model Linear-Cubic 2-1-31-22-2-222-22-2-22-2-2 () Effciency85.0678.4773.3568.1865.9362.69 (1.-1)and (-1,0)are the locations of smalles the mall iance instead of to locations of larger vari Efficiency100.0098.0695.4092.14845770.15 nce The D-optimal designs are nearly invarian heeomagiiwde much less variant to the magnitude of the dispersion effects.With either cri ticiencyoftheatanrdarddesigdecre and heuce the use of the standard desig Por the c-order model should be avoided if a severe dispersion effects case cethe lociarly optimal,while for more severe dispersion effects the ournal of Quality Technology Vol.29.No.1.January 1997 Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

OPTIMAL RESPONSE SURFACE DESIGNS IN THE PRESENCE OF DISPERSION EFFECTS 65 For the second-order model the D-optimal desig involve a shift of runs from the two locations of First-Order Model nearly equal quantities to the chosen locations.The 1-optimal designs are also highly invariant to changes TAelU5eLOatelPena0e5fcesfo Efficiency 100.00100.0010.00100.00100.00100.00 出设设语语超 First-Order Model 10.0010.00100.00100.00100.0010.00 Interaction Model Efficiency 100.0095.2088.3575.9963.3854.17 Efficiency10.0010.0010.0010.00100.00100.00 100.0091.137.6263.0650.4840.42 Efficiency100.00100.00100.00100.00100.00100.00 Interaction Model Second-Order Model 4040440-440-440-440 Doem Efficiency 100.00100.00100.0089.4470.7157.74 Efficiency 85.0676.0071.2467.1865.4563.41 4.0-4 30-42-0-30-0-00-0-0 1-3-1 1-3 Efficiency 100.0094.5582.1361.9642.9326.82 Efficiency 100.00100.00100.0094.0787.3778.99 Second-Order Model D-optimal designs involve a shift of runs from the edge 2-1-3 much more gradual in the case of the f-optimal de 85.0685.2284.6283.2780.8376.44 8 the efficiencies of the standard design,particularly 100.00973594.4491.889.5587.28 Vol.29,No.1.January 1997 Joural of Quality Technology Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

DARCY P.MAYS AND STEPHEN M.EASTER in the magnitude of the dispersion effects.Hence the models involve a shift of runs from the high vari- ianudardd For structure is identified and the experimenter believes effects both the D.and l-optimal designs are highl 1 of the ommended design. sign decrease dramatically as the severity of the dis Quadratic-Cubic The smallest variances are now located at the lov and high levels of X and the low and middle levels the 出接设语遇 increases,the optimal designs (both D First-Order Model fects cases the optimal designs are highh for milder dispersion efects gre Efficiency 100.0098.4894.5978.3065.5256.52 highly efficient (both D and for mild disp effects;however,with severe dispersion effects the are very low an sign similar to the optimal designs.The results for Efficiency 10.0097.1188.3071.3450.9036.15 the interaction mo de are nearly identical,with the Interaction Model For the second-order model,both the D.and are highly in Efficiency 100.0010.00100.0089.4470.7157.74 iant to the magnitude of the dispersion effe standard nid de though they remain fairly high even for severe dis 100.0096.5588.2470.8350.3734.87 practica Second-Order Model is close to ontimal in this case 2-2-22-0-22-0-220-220-21-02 Cubic-Cubic Efficiency 85.0680.7878.2176.2376.0074.67 locations of smallest variance,while the largest vari- I-Optimal ance occurs at (1, )Pr Design the others,and like the other cases as the disper sion effects increase the optimal designs for all three Efficiency 100.0096.1991.0784.2880.3175.66 oumal of Quality Technology Vol.29.No.1.January1997 Reproduced with permission of the copyright owner. Further reprodu ithout permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission

OPTIMAL RESPONSE SURFACE DESIGNS IN THE PRESENCE OF DISPERSION EFFECTS model.The D-and I-efficiencies of the standard de- the Cubi sign are again small in the severe dispersion effects For First-Order Model variance t to -0-4 A similar conclusion can be made for the -optimal designs,except the runs are allocated to the chosen 10.0095.1687.3661.3047.8231.95 the D more 19 the hom ogeneous variance case.and hence the stan dard design is extremely practical in this case The em 100.0089.0572.6946.9931.9317.35 and suggest that choosing a design closer to the Interaction Model is de Fortunately,for se rsion effects D-Optimal tothe magnitude of the dis and her Efficiency 10.00100.00100.0079.9957.743.33 Inverse Quadratic-Inverse Quadratic cture the lar ce is in the design A55 sown in Tab 7,fo Efficiency 100.0093.3377.4849.9331.9912.12 m the factori Second-Order Model severe disperson enects,both the D-and 22221-22-1-2220220220 -efficiencies of the standard design in thes severe Efficiency 85.0688.0790.3089.4989.0588.72 d for change 8o 2222228 240140 With the interact nodel the shift of runs t 21经1 the edge points and then the design center is more radual and both the l )and /-optimal designs are Efficiency 100.0097.2594.1791.8586.2979.17 ffects.The Dd gn are not as low as for the first-order model with of the /-eth ency for For the interaction model.the standard design is D-optimal for mild dispersion effects,and for severe stil ude the theoptimal d of the optimal designs,the shift of runs to the loca sign places few runs at the factorial locations Vol.29.No.1.January 1997 Journal of Quality Technology Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission
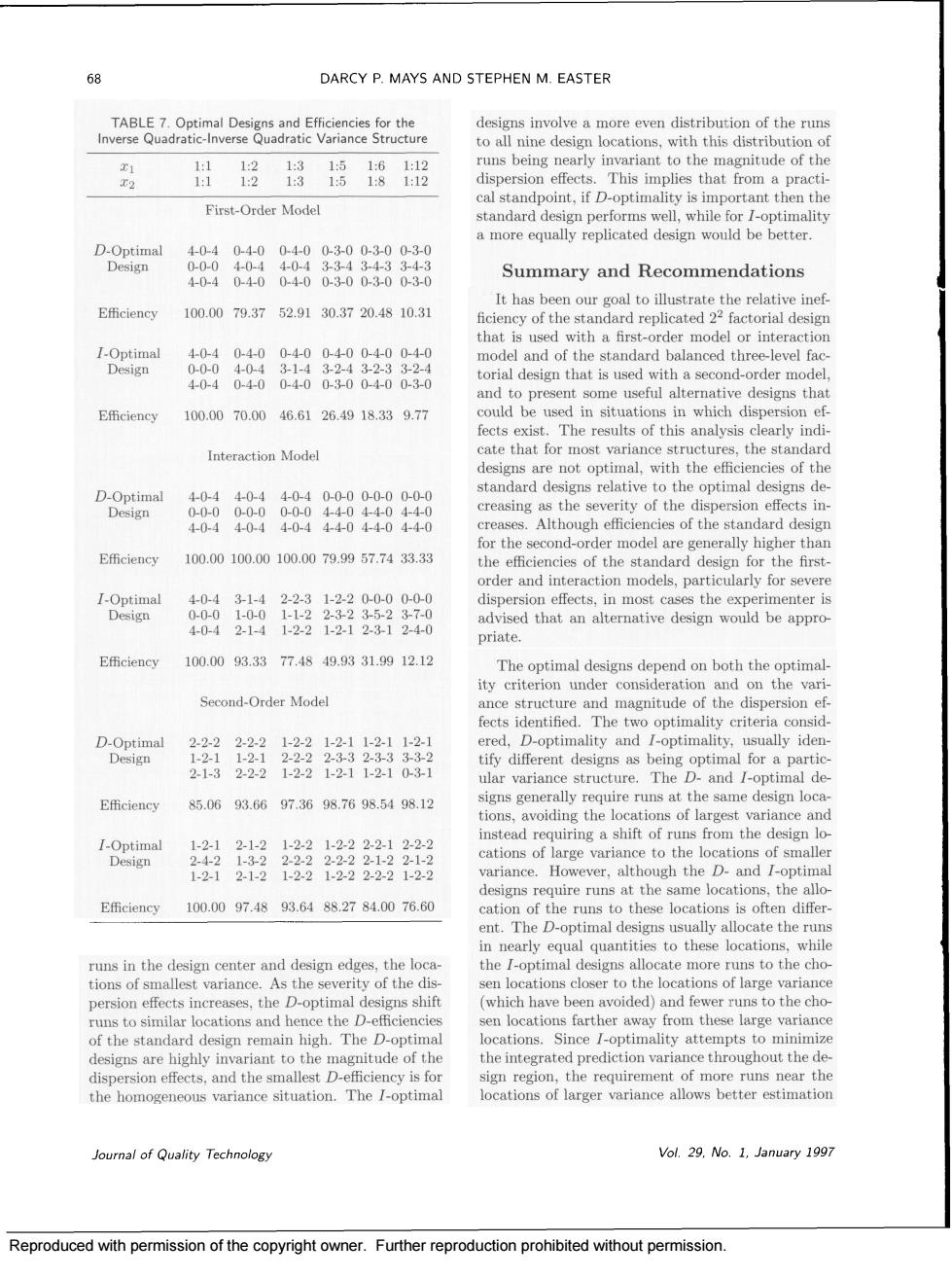
68 DARCY P.MAYS AND STEPHEN M.EASTER designs involve a more even distribution of the runs o all nine design locations,with this distribution of First-Order Model Summary and Recommendations Efficiency 100.0079.3752.9130.3720.4810.31 that is used with a first-order model or interaction -9e andofthestandard balanced three-level fa 0400400-30040030 and to present some useful alternative designs that Efficiency100.0070.0046.6126.4918.339.77 could be used in situations in which dispersion ef Interaction Model lesigns are not optimal,with the efficiencies of the Dpal tandard designs relative to the optimal de for the second-order model are generally higher than Efficiency 10.00100.0010.0079.957.7433.3 ncies of the standard d tor the firs advised that an alternative design would be appro- priate E用ciency100.0093.3377.4849.9331.9912.12 mal designs de end on both the optima Second-Order Model the dispersion ntimalit 232221221211-2-103 tify different designs as being optimal for a partic ar variance structure. Ihe D.and Efficiency 85.0693.6697.3698.7698.5498.12 the locations of largest instead requiring a shift of runs from the design lo- LOptimal ationsof t designs require runs at the same locations,the allo Efficiency 100.0097.4893.6488.2784.0076.60 cation of the runs t these location s is often differ e locations while runs in the design center and design edges,the loca the I-optimal designs allocate more runs to the cho tionsofne variance. ons closer to unsto locations nd heuce the D-eficlenci locations farther away from these large varianc of the standard design remain high.The D-optima ocations.Since T-optimality attempts to minimiz iesigsarehievarianttotepanitdeq s fo of m o runs near the the homogeneous variance situation.The /-optimal locations of larger variance allows better estimation Vol.29.No.1.January 1997 Reproduced with permission of the copyright owner.Further reproduction prohibited without permission
Reproduced with permission of the copyright owner. Further reproduction prohibited without permission