
第二章 热力学第一定律 【复习题】 【1】判断下列说法是否正确。 (1)状态给定后,状态函数就有一定的值,反之亦然。 (2)状态函数改变后,状态一定改变。 (3)状态改变后,状态函数一定都改变。 (4)因为△U=Qx,△H=Qp,所以Qx,Qp是特定条件下的状态函数。 (5)恒温过程一定是可逆过程。 (6)汽缸内有一定量的理想气体,反抗一定外压做绝热膨胀,则△H=Qp=0。 (7)根据热力学第一定律,因为能量不能无中生有,所以一个系统若要对外做功,必须从 外界吸收热量。 (8)系统从状态I变化到状态Ⅱ,若△T=0,则Q=0,无热量交换。 (9)在等压下,机械搅拌绝热容器中的液体,使其温度上升,则△H=Qp=0。 (10)理想气体绝热变化过程中,W=△U,即WR=△U=Cv△T,WR=△U=Cv△T,所以 WR=WIRe (11)有一个封闭系统,当始态和终态确定后: (a)若经历一个绝热过程,则功有定值: (b)若经历一个等容过程,则Q有定值(设不做非膨胀力): (c)若经历一个等温过程,则热力学能有定值: (d)若经历一个多方过程,则热和功的代数和有定值。 (12)某一化学反应在烧杯中进行,放热Q1,焓变为△H,若安排成可逆电池,使终态和 终态都相同,这时放热Q2,焓变为△H,则△H=△H。 【答】(1)正确,因为状态函数是体系的单质函数,体系确定后,体系的一系列状态函数 就确定。相反如果体系的一系列状态函数确定后,体系的状态也就被惟一确定。 (2)正确,根据状态函数的单值性,当体系的某一状态函数改变了,则状态函数必定发生 改变。 (3)不正确,因为状态改变后,有些状态函数不一定改变,例如理想气体的等温变化,内 能就不变。 (4)不正确,△H=Qp,只说明Qp等于状态函数H的变化值△H,仅是数值上相等,并 -1-
- 1 - 第二章 热力学第一定律 【复习题】 【1】 判断下列说法是否正确。 (1)状态给定后,状态函数就有一定的值,反之亦然。 (2)状态函数改变后,状态一定改变。 (3)状态改变后,状态函数一定都改变。 (4)因为△U=Qv, △H =Qp,所以 Qv,Qp 是特定条件下的状态函数。 (5)恒温过程一定是可逆过程。 (6)汽缸内有一定量的理想气体,反抗一定外压做绝热膨胀,则△H= Qp=0。 (7)根据热力学第一定律,因为能量不能无中生有,所以一个系统若要对外做功,必须从 外界吸收热量。 (8)系统从状态Ⅰ变化到状态Ⅱ,若△T=0,则 Q=0,无热量交换。 (9)在等压下,机械搅拌绝热容器中的液体,使其温度上升,则△H = Qp = 0。 (10)理想气体绝热变化过程中,W=△U,即 WR=△U=CV△T,WIR=△U=CV△T,所以 WR=WIR。 (11)有一个封闭系统,当始态和终态确定后; (a)若经历一个绝热过程,则功有定值; (b)若经历一个等容过程,则 Q 有定值(设不做非膨胀力); (c)若经历一个等温过程,则热力学能有定值; (d)若经历一个多方过程,则热和功的代数和有定值。 (12)某一化学反应在烧杯中进行,放热 Q1,焓变为△H1,若安排成可逆电池,使终态和 终态都相同,这时放热 Q2,焓变为△H2,则△H1=△H2。 【答】(1)正确,因为状态函数是体系的单质函数,体系确定后,体系的一系列状态函数 就确定。相反如果体系的一系列状态函数确定后,体系的状态也就被惟一确定。 (2)正确,根据状态函数的单值性,当体系的某一状态函数改变了,则状态函数必定发生 改变。 (3)不正确,因为状态改变后,有些状态函数不一定改变,例如理想气体的等温变化,内 能就不变。 (4)不正确,ΔH=Qp,只说明 Qp 等于状态函数 H 的变化值 ΔH,仅是数值上相等,并

不意味着Qp具有状态函数的性质。△H=Qp只能说在恒压而不做非体积功的特定条件下, Qp的数值等于体系状态函数H的改变,而不能认为Qp也是状态函数。 (5)正确,因为恒温过程是体系与环境的温度始终保持相等且恒定,是一个自始至终保热 平衡的过程,由于只有同时满足力学平衡、相平衡、化学平衡才能保持热平衡,所以这种过 程必然是一个保持连续平衡状态的过程,即为可逆过程。恒温过程不同与等温过程,后者只 需始终态温度相同即可,而不管中间经历的状态如何。等温可逆过程则一定是恒温过程。 (6)不正确,因为这是外压一定,不是体系的压力一定,绝热膨胀时,Q=0,不是Q=0。 绝热膨胀后,p20,使其 △H≠Qp。 (10)不正确,虽然不管是否可逆,W=△U=Cv△T,但可逆与不可逆过程的最终温度不同, 所以WR≠WR。 (11)(a)正确,因为始终态确定后,△U就确定,又是绝热过程,则Q=0,根据热力学 第一定律,W=△U有定值: (b)正确,因为始终态确定后,△U就确定,又是等容过程,则W=0,根据热力学第一定 律,Q=△U有定值: (c)不正确,只有理想气体的等温过程,热力学能才有定值: (d)正确,因为始终态确定后,△U就确定,即热和功的代数和有定值。 (12)正确,因为体系的始终态确定后,可以通过不同的过程来实现,一般在不同的过程中 W、Q的数值不同,但焓是状态函数,而状态函数的变化与过程无关。即△H=△H。 【2】回答下列问题。 (1)在盛水槽中放置一个盛水的封闭试管,加热盛水槽中之水,使其达到沸点。试问试管 中的水是否会沸腾,为什么? (2)夏天将室内电冰箱的门打开,接通电源并紧闭门窗(设墙壁、门窗都不传热),能否 使室内温度降低,为什么? (3)可逆热机的效率最高,在其他条件都相同的前提下,用可逆热机去牵引火车,能否使 火车的速度加快,为什么? -2-
- 2 - 不意味着 Qp 具有状态函数的性质。ΔH=Qp 只能说在恒压而不做非体积功的特定条件下, Qp 的数值等于体系状态函数 H 的改变,而不能认为 Qp 也是状态函数。 (5)正确,因为恒温过程是体系与环境的温度始终保持相等且恒定,是一个自始至终保热 平衡的过程,由于只有同时满足力学平衡、相平衡、化学平衡才能保持热平衡,所以这种过 程必然是一个保持连续平衡状态的过程,即为可逆过程。恒温过程不同与等温过程,后者只 需始终态温度相同即可,而不管中间经历的状态如何。等温可逆过程则一定是恒温过程。 (6)不正确,因为这是外压一定,不是体系的压力一定,绝热膨胀时,Q=0,不是 Qp=0。 绝热膨胀后,p2<p1,T2<T1,理想气体的焓是温度的函数,所以该过程中△H<0。 (7)不正确,因为还可以降低体系的温度来对外作功。 (8)不正确,因为△T=0 时只能说明体系的内能不变,而根据热力学第一定律,只有当功 为零的时候,热才是零。 (9)不正确,在等压下,机械搅拌绝热容器中的液体,是环境对体系做功,Wf>0,使其 △H ≠ Qp。 (10)不正确,虽然不管是否可逆,WR=△U=CV△T,但可逆与不可逆过程的最终温度不同, 所以 WR≠WIR。 (11)(a)正确,因为始终态确定后,△U 就确定,又是绝热过程,则 Q=0,根据热力学 第一定律,W=△U 有定值; (b)正确,因为始终态确定后,△U 就确定,又是等容过程,则 W=0,根据热力学第一定 律, Q=△U 有定值; (c)不正确,只有理想气体的等温过程,热力学能才有定值; (d)正确,因为始终态确定后,△U 就确定,即热和功的代数和有定值。 (12)正确,因为体系的始终态确定后,可以通过不同的过程来实现,一般在不同的过程中 W、Q 的数值不同,但焓是状态函数,而状态函数的变化与过程无关。即△H1=△H2。 【2】回答下列问题。 (1)在盛水槽中放置一个盛水的封闭试管,加热盛水槽中之水,使其达到沸点。试问试管 中的水是否会沸腾,为什么? (2)夏天将室内电冰箱的门打开,接通电源并紧闭门窗(设墙壁、门窗都不传热),能否 使室内温度降低,为什么? (3)可逆热机的效率最高,在其他条件都相同的前提下,用可逆热机去牵引火车,能否使 火车的速度加快,为什么?

(4)Zn与稀硫酸作用,(a)在敞口的容器中进行:(b)在密闭的容器中进行。哪一种情况 放热较多,为什么? (5)在一铝制筒中装有压缩空气,温度与环境平衡。突然打开筒盖,使气体冲出,当压力 与外界相等时,立即盖上筒盖,过一会儿,筒中气体压力有何变化? (6)在N2和N1的物质的量之比为1:3的反应条件下合成氨,实验测得在温度T1和T2 时放出的热量分别为Qp(T)和Qp(T2),用Kirchhoff定律验证时,与下述公式的 计算结果不符,试解释原因。△L()-△H(T+A,Cdn (7)从同一始态A出发,经历三种不同途径到达不同的终态:(1)经等温可逆过程从A→B: (2)经绝热可逆过程从A→C:(3)经绝热不可逆过程从A→D。试问: (a)若使终态的体积相同,D点应位于BC虚线的什么位置,为什么? (b)若使终态的压力相同,D点应位于BC虚线的什么位置,为什么,参见图2.16。 (8)在一个玻璃瓶中发生如下反应:H2(g)+C1,(g)m→2HC1(g) PA (a) (b) 图2.16 反应前后T,,V均未发生变化,设所有的气体都可以看作是理想气体。因为理想气体的热力 学能仅是温度的函数,U=U(T),所以该反应的△U=0。这个结论对不对?为什么? 【答】(1)不会,因为要使液体沸腾,必须有一个大于沸点的环境热源,而槽中水的温度 与试管中水的沸点温度相同无法使其沸腾。 (2)不能,因为将室内看成是一个绝热的封闭体系,接通电源后相当于环境对体系做电功 W,Qv=O:We=0;△U=Qv+W+W=W>0,所以室内温度将会升高,而不是降低。 (3)不能,因为可逆热机的效率是指热效率,即热转换为功的效率,而不是运动速率,热 力学没有时间的坐标,所以没有速度的概念,而可逆途径的特点之一就是变化无限缓 慢,所以只能使火车的速度减慢而不能加快火车的速度。 (4)在密闭的容器中放热较多,因为Z与稀硫酸作用,在敞口的容器中进行时放出的热 -3-
- 3 - (4)Zn 与稀硫酸作用,(a)在敞口的容器中进行;(b)在密闭的容器中进行。哪一种情况 放热较多,为什么? (5)在一铝制筒中装有压缩空气,温度与环境平衡。突然打开筒盖,使气体冲出,当压力 与外界相等时,立即盖上筒盖,过一会儿,筒中气体压力有何变化? (6)在 N2 和 N1 的物质的量之比为 1 :3 的反应条件下合成氨,实验测得在温度 T1 和 T2 时放出的热量分别为 QP(T1)和 QP(T2),用 Kirchhoff 定律验证时,与下述公式的 计算结果不符,试解释原因。△rHm(T2)=△rHm(T1)+ 2 1 T r P T C dT (7)从同一始态 A 出发,经历三种不同途径到达不同的终态:(1)经等温可逆过程从 A→B; (2)经绝热可逆过程从 A→C;(3)经绝热不可逆过程从 A→D。试问: (a)若使终态的体积相同,D 点应位于 BC 虚线的什么位置,为什么? (b)若使终态的压力相同,D 点应位于 BC 虚线的什么位置,为什么,参见图 2.16。 (8)在一个玻璃瓶中发生如下反应: 2 2 ( ) ( ) 2 ( ) hv H g Cl g HCl g + ⎯⎯→ p V p O V O V1 V2 p1 p2 A B C A C B (a) (b) 图 2.16 反应前后 T,p,V 均未发生变化,设所有的气体都可以看作是理想气体。因为理想气体的热力 学能仅是温度的函数,U=U(T),所以该反应的△U=0。这个结论对不对?为什么? 【答】(1)不会,因为要使液体沸腾,必须有一个大于沸点的环境热源,而槽中水的温度 与试管中水的沸点温度相同无法使其沸腾。 (2)不能,因为将室内看成是一个绝热的封闭体系,接通电源后相当于环境对体系做电功 Wf,QV=0;We=0; △U=QV+ We+ Wf= Wf>0,所以室内温度将会升高,而不是降低。 (3)不能,因为可逆热机的效率是指热效率,即热转换为功的效率,而不是运动速率,热 力学没有时间的坐标,所以没有速度的概念,而可逆途径的特点之一就是变化无限缓 慢,所以只能使火车的速度减慢而不能加快火车的速度。 (4)在密闭的容器中放热较多,因为 Zn 与稀硫酸作用,在敞口的容器中进行时放出的热

为Qp,在密闭的容器中进行时放出的热为Qv,而Qp=Qv+△nRT,△n=1,Qp和Qv 均为负值,所以Qv>Qr。 (5)压缩空气突然冲出筒外,可视为决热膨胀过程,终态为室内气压,筒内温度降低, 盖上筒盖,过一会儿,温度升至室温,压力大于p。 (6)Kirchhoff定律中的△Hm(T2)和△Hm(Ti)是按反应计量系数完全进行到底,即=lmol 时的热效应,实验测得的热量是反应达到平衡时放出的热量,即飞(绝热不可逆)>p2(绝热可 逆) 当p2相同时,D点在B、C之间,V2(等温可逆)>V2(绝热不可逆)>V2(绝热 可逆)。 (8)由热力学第一定律:dU=6Q+6W=8Q+δW。+6W,,而6Q=0,体积没有变, 所以6W。=0,8W,为非体积功,在该反应中v为光能,是另一种形式的功,所以 dU≠0,所以该判断不对。 【3】.可逆过程有哪些基本特征?请识别下列过程中哪些是可逆过程。 (1)摩擦生热: (2)室温和大气压力(101.3kPa)下,水蒸发为同温、同压的气: (3)373K和大气压力(101.3kPa)下,水蒸发为同温、同压的气: (4)用于电池使灯泡发光: (5)用对消法测可逆电池的电动势: -4
- 4 - 为 QP,在密闭的容器中进行时放出的热为 QV,而 QP=QV+△n(RT),△n=1,QP和 QV 均为负值,所以|QV|>|QP| 。 (5)压缩空气突然冲出筒外,可视为决热膨胀过程,终态为室内气压 p θ ,筒内温度降低, 盖上筒盖,过一会儿,温度升至室温,压力大于 p θ 。 (6) Kirchhoff 定律中的△rHm(T2)和△rHm(T1)是按反应计量系数完全进行到底,即 ξ=1mol 时的热效应,实验测得的热量是反应达到平衡时放出的热量,即 ξ<1mol,它们之间 的关系为△rHm =△rH /ξ ,所以△rH 的值不符合 Kirchhoff 定律。 (7)从同一始态出发经一绝热可逆膨胀过程和一经绝热不可逆膨胀过程,当到达相同的终 态体积 V2 或相同的终态压力 p2 时,绝热可逆过程比绝热不可逆过程作功大,又因为 W(绝热)=CV(T2-T1),所以 T2(绝热不可逆)大于 T2(绝热可逆),在 V2 相同 时,p=nRT/V,则 p2(绝热不可逆)大于 p2(绝热可逆)。在终态 p2 相同时,V =nRT/p , V2(绝热不可逆)大于 V2(绝热可逆)。 不可逆过程与等温可逆过程相比较:由于等温可逆过程温度不变,绝热膨胀温度下降, 所以 T2(等温可逆)大于 T2(绝热不可逆);在 V2 相同时, p2(等温可逆)大于 p2 (绝热不可逆)。在 p2 相同时,V2(等温可逆)大于 V2(绝热不可逆)。 综上所述,从同一始态出发经三种不同过程, 当 V2 相同时,D 点在 B、C 之间,p2(等温可逆)>p2(绝热不可逆)> p2(绝热可 逆) 当 p2 相同时,D 点在 B、C 之间,V2(等温可逆)> V2(绝热不可逆)>V2(绝热 可逆)。 (8)由热力学第一定律: e f dU Q W Q W W = + = + + ,而 Q = 0 ,体积没有变, 所以 0 We = , Wf 为非体积功,在该反应中 h 为光能,是另一种形式的功,所以 dU 0 ,所以该判断不对。 【3】.可逆过程有哪些基本特征?请识别下列过程中哪些是可逆过程。 (1)摩擦生热; (2)室温和大气压力(101.3 kPa)下,水蒸发为同温、同压的气; (3)373K 和大气压力(101.3kPa)下,水蒸发为同温、同压的气; (4)用于电池使灯泡发光; (5)用对消法测可逆电池的电动势;

(6)N2(g),O2(g)在等温、等压下温和: (7)恒温下将1mol水倾入大量溶液中,溶液浓度不变: (8)水在冰点时变成同温同压的冰。 答:可逆过程基本特征:(1)过程以无限小变化进行,由一连串接近于平衡的状态构 成:(2)在反向过程中必须沿着原来过程的逆过程用同样的手续使体系和环境复原:(3) 等温可逆膨胀过程中体系对环境做最大功,等温可逆压缩过程中环境对体系做最小功。 只有(3)、(5)和(8)是可逆过程,其余过程均为不可逆过程。 【4】试将如下的两个不可逆过程设计成可逆过程: (1)在298K,101.3Pa压力下,水蒸发为同温、同压的气: (2)在268K,101.3kPa压力下,水凝结为同温、同压的冰。 解(1)设计过程如下: H20(1,298K,Ps)e→H20(g,298K,Ps) d H20(1,298K,101.3kPaH20(g,298K,101.3kPa) a c H20(L,373K,101.3kPa)b→H20g.373K,101.3kPa) a为等压可逆升温:b为可逆等温等压蒸发:c为等压可逆降温。 或经过d、e、f过程 d为可逆等温降压,Ps为水在298K时的饱和蒸汽压: e为可逆等温等压蒸发:f为可逆等温升压。 (2)设计过程如下: H20(I,268K,101.3kPaH20(s,268K,101.3kPa) a H20(273K,101.3kPa)b→H20s.273K,101.3kPa) a为等压可逆升温:b为可逆等温等压相变:c为等压可逆降温。 【5】判断下列各过程中的Q,W,△U和可能知道的△H值,用>0,<0或=0表示. (1)如图2.17所示,当电池放电后,选择不同的对象为研究系统, ①以水和电阻丝为系统 ②以水为系统 ∧V ③以电阻丝为系统 图2.17 -5-
- 5 - (6)N2(g),O2(g)在等温、等压下温和; (7)恒温下将 1 mol 水倾入大量溶液中,溶液浓度不变; (8)水在冰点时变成同温同压的冰。 答:可逆过程基本特征:(1)过程以无限小变化进行,由一连串接近于平衡的状态构 成;(2)在反向过程中必须沿着原来过程的逆过程用同样的手续使体系和环境复原;(3) 等温可逆膨胀过程中体系对环境做最大功,等温可逆压缩过程中环境对体系做最小功。 只有(3)、(5)和(8)是可逆过程,其余过程均为不可逆过程。 【4】试将如下的两个不可逆过程设计成可逆过程: (1)在 298K,101.3kPa 压力下,水蒸发为同温、同压的气; (2)在 268K,101.3kPa 压力下,水凝结为同温、同压的冰。 解 (1)设计过程如下: H2O (l,298K,PS) H2O (g,298K,PS) H2O (l,298K,101.3kPa) H2O (g,298K,101.3kPa) H2O (l,373K,101.3kPa) H2O (g,373K,101.3kPa) a b c d e f a 为等压可逆升温;b 为可逆等温等压蒸发;c 为等压可逆降温。 或经过 d、e、f 过程 d 为可逆等温降压,PS为水在 298K 时的饱和蒸汽压; e 为可逆等温等压蒸发;f 为可逆等温升压。 (2)设计过程如下: H2O (l,268K,101.3kPa) H2O (s,268K,101.3kPa) H2O (l,273K,101.3kPa) H2O (s,273K,101.3kPa) a b c a 为等压可逆升温;b 为可逆等温等压相变;c 为等压可逆降温。 【5】判断下列各过程中的 Q,W,△U 和可能知道的△H 值,用>0,<0 或=0 表示. (1)如图 2.17 所示,当电池放电后,选择不同的对象为研究系统, ①以水和电阻丝为系统 ②以水为系统 ③以电阻丝为系统 图 2.17
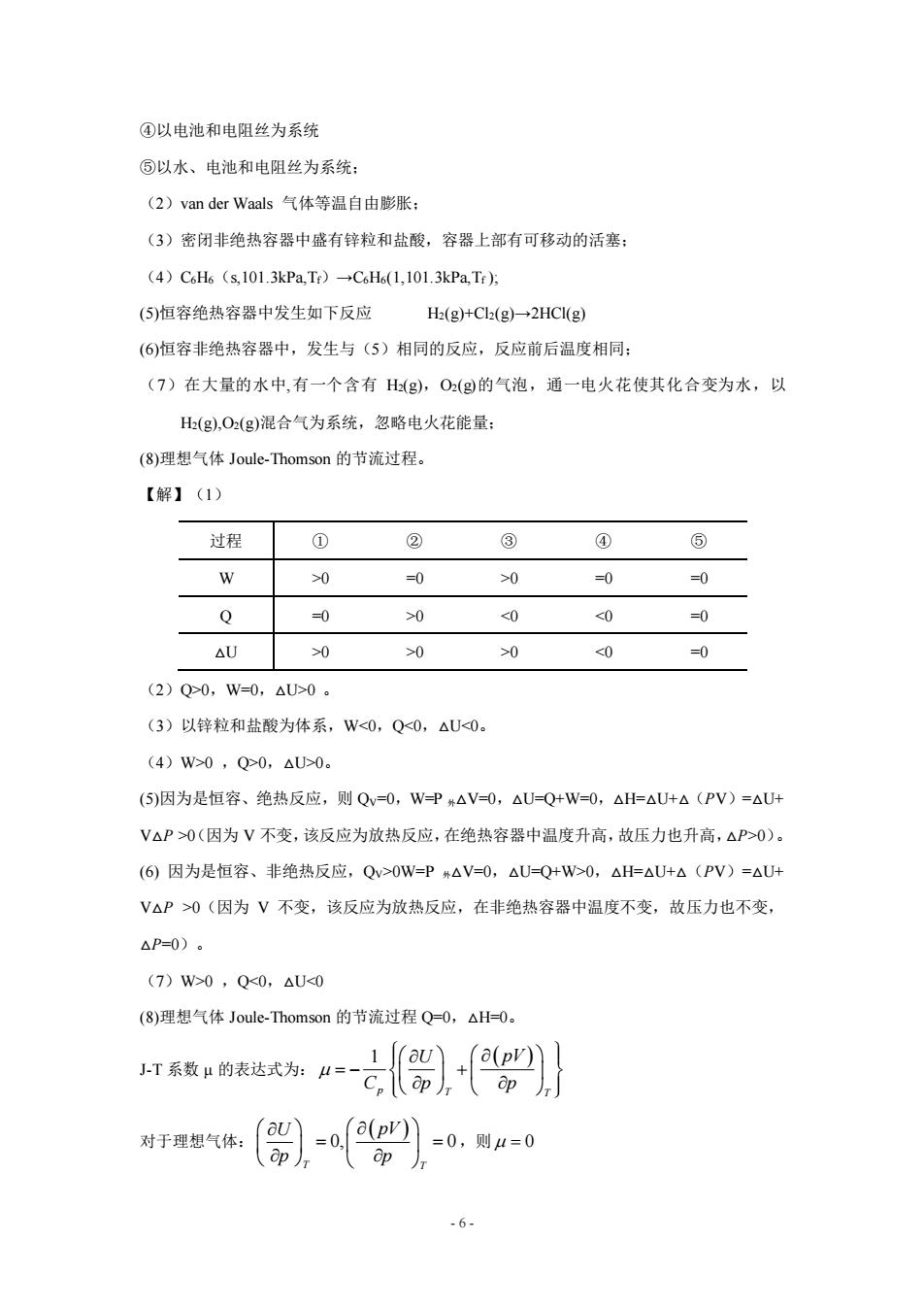
④以电池和电阻丝为系统 ⑤以水、电池和电阻丝为系统: (2)van der Waals气体等温自由膨胀: (3)密闭非绝热容器中盛有锌粒和盐酸,容器上部有可移动的活塞: (4)C6H6(s,101.3Pa,Tr)→C6H6(1,101.3kPa,Tf)方 (5)恒容绝热容器中发生如下反应 H(g)+C2(g)→2HCI(g) (6)恒容非绝热容器中,发生与(5)相同的反应,反应前后温度相同: (7)在大量的水中,有一个含有H(g),O2(g的气泡,通一电火花使其化合变为水,以 H(g),O2(g)混合气为系统,忽略电火花能量: (8)理想气体Joule--Thomson的节流过程。 【解】(1) 过程 ① ② ③ ④ ⑤ W 0 =0 >0 =0 =0 Q =0 >0 0 >0 >0 0,W=0,△0U>0。 (3)以锌粒和盐酸为体系,W0,Q>0,△U>0。 (5)因为是恒容、绝热反应,则Qv=0,W=P#△V=0,△U=Q+W=0,△H=△U+△(PV)=△U+ V△P>0(因为V不变,该反应为放热反应,在绝热容器中温度升高,故压力也升高,△P>0)。 (6)因为是恒容、非绝热反应,Qv>0W=P#△V=0,△U=Q+W>0,△H=△U+△(PV)=△U+ V△P>0(因为V不变,该反应为放热反应,在非绝热容器中温度不变,故压力也不变, △P=0)。 (7)W>0,Q<0,△U<0 (8)理想气体Joule-Thomson的节流过程Q=O,△H=0。 灯系数的表达式海A=七品)十四》 对于理想气体: -6
- 6 - ④以电池和电阻丝为系统 ⑤以水、电池和电阻丝为系统; (2)van der Waals 气体等温自由膨胀; (3)密闭非绝热容器中盛有锌粒和盐酸,容器上部有可移动的活塞; (4)C6H6(s,101.3kPa,Tf)→C6H6(1,101.3kPa,Tf ); (5)恒容绝热容器中发生如下反应 H2(g)+Cl2(g)→2HCl(g) (6)恒容非绝热容器中,发生与(5)相同的反应,反应前后温度相同; (7)在大量的水中,有一个含有 H2(g),O2(g)的气泡,通一电火花使其化合变为水,以 H2(g),O2(g)混合气为系统,忽略电火花能量; (8)理想气体 Joule-Thomson 的节流过程。 【解】(1) (2)Q>0,W=0,△U>0 。 (3)以锌粒和盐酸为体系,W0 ,Q>0,△U>0。 (5)因为是恒容、绝热反应,则 QV=0,W=P 外△V=0,△U=Q+W=0,△H=△U+△(PV)=△U+ V△P >0(因为 V 不变,该反应为放热反应,在绝热容器中温度升高,故压力也升高,△P>0)。 (6) 因为是恒容、非绝热反应,QV>0W=P 外△V=0,△U=Q+W>0,△H=△U+△(PV)=△U+ V△P >0(因为 V 不变,该反应为放热反应,在非绝热容器中温度不变,故压力也不变, △P=0)。 (7)W>0 ,Q0 =0 >0 =0 =0 Q =0 >0 0 >0 >0 <0 =0

又因为4= OT 所以dT=0,理想气体的内能是温度的函数。 △U=0,W=△U-Q=0 【6】请列举4个不同类型的等焓过程。 例:(1)Joule-Thomson的节流过程:(2)理想气体的等温过程:(3)绝热等压反应(非 体积功为0)(4)理想气体的自由膨胀过程 【7】在下列关系式中,请指出哪几个是准确的,哪几个是不准确的,并简单说明理由。 (1)△.H(石墨,S)=△H(CO2.8) (2)△.H(H2,g)=△HR(HO,g) (3)△.HR(N2,g)=△H(2NO2g), (4)△.H(SO2,8)=0, (5)△rH(H2O,g)=△,H(H2O,1)+△mH(H2O,1) (6)△.H(02,g)=△H(H2O,1)。 解(1)准确,因为碳的最稳定单质是石墨固体,而1摩尔石墨完全燃烧生成1摩尔二氧 化碳气体。 (2)不准确,因为氢气完全燃烧的指定产物是液态的水,而不是气态的水。 (3)不准确,根据反应N2+2O,=2NO,的计量系数,可得: A.HN2,g)=2△H(NO2.g),而不是△.HN2,g)=△yH(2NO2.g) (4)不准确,因为SO,还可以燃烧生成SO,所以△.H(SO2,g)≠0。 (5)准确,根据下列变化可得△H但2O,g)=△,H(H2O,)+△pH(H2O,) H2g+0.5020)△rH8(H20g) H20(g) △fH品(H2O,D H2o0△vapm(H20,0 (6)不准确,因为△.H(H2,g)=△H(HO,1),而不是△.H(02,g)=△H(H2O,) 【8】Cpm是否恒大于Cvm?有一个化学反应,所有的气体都可以作为理想气体处理,若 反应的△Cpm>0,则反应的△Cvm也一定大于零吗? -7-
- 7 - 又因为 H T p = 所以 dT = 0 ,理想气体的内能是温度的函数。 △U=0,W=△U-Q=0 【6】请列举 4 个不同类型的等焓过程。 例:(1)Joule-Thomson 的节流过程;(2)理想气体的等温过程;(3)绝热等压反应(非 体积功为 0)(4)理想气体的自由膨胀过程 【7】在下列关系式中,请指出哪几个是准确的,哪几个是不准确的,并简单说明理由。 (1) 2, ( , ) ( ) c m f m H s H CO g = 石墨 , (2) 2 ( , ) ( , ) c m f m H g H H O g = 2 H , (3) 2, ( , ) (2 ) c m f m H g H NO g = 2 N , (4) 2 ( , ) 0 c m H SO g = , (5) 2 2 ( , ) ( ,1) ( ,1) f m f m vap m H O g H H O H H O = + 2 H , (6) 2 ( , ) ( ,1) c m f m H g H H O = 2 O 。 解 (1)准确,因为碳的最稳定单质是石墨固体,而 1 摩尔石墨完全燃烧生成 1 摩尔二氧 化碳气体。 (2) 不准确,因为氢气完全燃烧的指定产物是液态的水,而不是气态的水。 (3) 不准确,根据反应 2 2 N2 + = 2 2 O NO 的计量系数,可得: 2, ( , ) 2 ( ) c m f m H g H NO g = 2 N ,而不是 2, ( , ) (2 ) c m f m H g H NO g = 2 N (4) 不准确,因为 2 SO 还可以燃烧生成 3 SO ,所以 2 ( , ) 0 c m H SO g 。 (5) 准确,根据下列变化可得 2 2 ( , ) ( ,1) ( ,1) c m f m vap m H O g H H O H H O = + 2 H H2(g)+0.5O2(g) H2O(g) H2O(l) f Hm (H2O,g) fHm (H2O,l) Hm(H2O,l) vap (6) 不准确,因为 2 ( , ) ( ,1) c m f m H g H H O = 2 H ,而不是 2 ( , ) ( ,1) c m f m H g H H O = 2 O 【8】Cp,m是否恒大于 Cv,m?有一个化学反应,所有的气体都可以作为理想气体处理,若 反应的△Cp,m>0,则反应的△Cv,m也一定大于零吗?

【解】(1)Cpm不一定恒大于Cvm。气体的Cpm和Cvm的关系为: m 上式的物理意义如下: 恒容时体系的体积不变,而恒压时体系的体积随温度的升高要发生变化。 av (1)p 项表示,当体系体积变化时外界所提供的额外能量: aT 项表示,由于体系的体积增大,使分子间的距离增大,位能增大,使 热力学能增大所需的能量: aU 由于p和 m 都为正值,所以Cpm与C,m的差值的正负就取决于 m 项。如果体 av 系的体积随温度的升高而增大, 则 m 0,则Cpm>Cm:反之, 体系的体积随温 度的升高而缩小的话 aT 0:只有少数流体在某些温度范围内 aT 0,反应的△Cvm不一定大于零。 -8-
- 8 - 【解】(1)Cp,m不一定恒大于 Cv,m。气体的 Cp,m和 Cv,m的关系为: m m p, , m p p m V m T U V C C V T = + - 上式的物理意义如下: 恒容时体系的体积不变,而恒压时体系的体积随温度的升高要发生变化。 (1) m p p V T 项表示,当体系体积变化时外界所提供的额外能量; (2) m m m T p U V V T 项表示,由于体系的体积增大,使分子间的距离增大,位能增大,使 热力学能增大所需的能量; 由于 p 和 m m T U V 都为正值,所以 Cp,m 与 CV m, 的差值的正负就取决于 m p V T 项。如果体 系的体积随温度的升高而增大,则 m p 0 V T ,则 C C p, , m V m ;反之,体系的体积随温 度的升高而缩小的话, m p 0 V T ,则 C C p, , m V m。 通常情况下,大多数流体(气体和液体)的 m p 0 V T ;只有少数流体在某些温度范围内 m p 0 V T ,如水在 0~4℃的范围内,随温度升高体积是减小的,所以 C C p, , m V m 。 对于理想气体,则有 C C R p, , m V m - = 。 (2)对于气体都可以作为理想气体处理的化学反应,则有 C C R p, , m V m B B = + 即 C C R V m m , p, B B = - 所以,若反应的△Cp,m>0, 反应的△Cv,m不一定大于零

习题解答 【1】如果一个系统从环境吸收了40J的热,而系统的热力学能却增加了200,问系统 从环境得到了多少功?如果该系统在膨胀过程中对环境作了10kJ的功,同时吸收了28k的 热,求系统的热力学能变化值。 【解】 W=△U-O=200J-40J=160J AU=Q+W=28kJ+(-10kJ)=18kJ 【2】有10mol的气体(设为理想气体),压力为1000kPa,温度为300K,分别求出温 度时下列过程的功: (1)在空气压力为100kPa时,体积胀大1dm3: (2)在空气压力为100kPa时,膨胀到气体压力也是100kpa; (3)等温可逆膨胀至气体的压力为100kPa 【解】(1)气体作恒外压膨胀:W=-P外△V故 W=-P9△V=-100×10Pa×(1×103)m3=.100J (2)W=-P9△V=-P8 nRT nRT P =-10mol×8.314J-K-1.mol1×300K 100KPa =.22.45KJ 1000KPa (3)W =-nRT In =-nRT in V P 1000KPa =.10mol×8.314JK-1mo×300K×h 100KPa =.57.43kJ 3 【3】1mol单原子理想气体,Cv,m=亏R,始态(1)的温度为273K,体积为22.4dm3, 2 经历如下三步,又回到始态,请计算每个状态的压力、Q、W和△U。 (1)等容可逆升温由始态(1)到546K的状态(2): (2)等温(546K)可逆膨胀由状态(2)到44.8dm3的状态(3): (3)经等压过程由状态(3)回到始态(1)。 【解】(1)由于是等容过程,则 W1=0 -9-
- 9 - 习题解答 【1】如果一个系统从环境吸收了 40J 的热,而系统的热力学能却增加了 200J,问系统 从环境得到了多少功?如果该系统在膨胀过程中对环境作了 10kJ 的功,同时吸收了 28kJ 的 热,求系统的热力学能变化值。 【解】 W=ΔU-Q=200J-40J=160J ΔU=Q+W=28kJ+(-10kJ)=18kJ 【2】有 10mol 的气体(设为理想气体),压力为 1000kPa,温度为 300K,分别求出温 度时下列过程的功: (1)在空气压力为 100kPa 时,体积胀大 1dm3; (2)在空气压力为 100kPa 时,膨胀到气体压力也是 100kpa; (3)等温可逆膨胀至气体的压力为 100kPa. 【解】(1)气体作恒外压膨胀: W = −P外V 故 W = −P V =-100×103Pa×(1×10-3)m3=-100J (2) = − = − = − − 1 2 2 1 1 P P nRT P nRT P nRT W P V P =-10mol×8.314J·K-1·mol-1×300K − KPa KPa 1000 100 1 =-22.45KJ (3) 2 1 1 2 ln ln P P nRT V V W = −nRT = − =-10mol×8.314J·K-1·mol-1×300K× KPa KPa 100 1000 ln =-57.43kJ 【3】1mol 单原子理想气体, CV m R 2 3 , = ,始态(1)的温度为 273K,体积为 22.4dm3, 经历如下三步,又回到始态,请计算每个状态的压力、Q、W 和 ΔU。 (1)等容可逆升温由始态(1)到 546K 的状态(2); (2)等温(546K)可逆膨胀由状态(2)到 44.8dm3 的状态(3); (3)经等压过程由状态(3)回到始态(1)。 【解】 (1)由于是等容过程,则 W1=0

R℃_1×8314×273=101.325KPa P1= V22.4×10-3 h=nRg-1×8314×546 22.4×10-3 202.65KPa AU1=Q+W1=Q=∫CvdT-∫nCv.mdT=nCvn(亿2-T) =1×3/2×8.314(546-273)=3404.58J (2)由于是等温过程,则 △U2=0 根据△U=Q+W得Q2=W2 又根据等温可逆过程得: wg=-mR7h5=-1×8314×546h448-3146.5J V 22.4 Q2=-W2=3146.5J (3).p3= nR℃3-1×8.314×546」 V344.8×10-3 101.325KPa 由于是循环过程则:△U=△U1+△U2+△U3=0 得△03=-(△U1+AU2)=-△U1=-3404.58J W3=-P△V=-P3(V3-V1)=101325×(0.0224-0.0448)=2269.68J Q3=△U3-W3=-3404.58J-2269.68J=-5674.26J 【4】在291K和100kPa下,1 molZn(s)溶于足量稀盐酸中,置换出1molH(g),并放热 152K」J。若以Zn和盐酸为系统,求该反应所做的功及系统热力学能的变化。 解该反应 Zn(s)+2HCl(a)=ZnCl2(s)+H2(g) 所以 W=一P外△V=p生成物-'反应物)≈pVH2 =-1mol×8.314J●K-1●mol-1×291K=-2.42kJ △U=Q+W=-152-2.42=-154.4kJ 【5】在298K时,有2molN2(g,始态体积为15dm,保持温度不变,经下列三个过程 膨胀到终态体积为50dm3,计算各过程的△U,△H,W和Q的值。设气体为理想气体。 (1)自由膨胀: (2)反抗恒外压100kPa膨胀: -10-
- 10 - KPa V nRT p 101.325 22.4 10 1 8.314 273 3 1 1 1 = = = − KPa V nRT p 202.65 22.4 10 1 8.314 546 3 1 2 2 = = = − ΔU1=Q1+W1=Q1= ( ) CV dT = nCV ,m dT = nCV ,m T2 −T1 =1×3/2×8.314(546-273)=3404.58J (2) 由于是等温过程,则 ΔU2=0 根据 ΔU=Q+W 得 Q2=-W2 又根据等温可逆过程得: W2= J V V nRT 3146.5 22.4 44.8 ln 1 8.314 546ln 2 3 − = − = − Q2=-W2=3146.5J (3). KPa V nRT p 101.325 44.8 10 1 8.314 546 3 3 3 3 = = = − 由于是循环过程则:ΔU=ΔU1+ΔU2+ΔU3=0 得 ΔU3=-(ΔU1+ΔU2)=-ΔU1=-3404.58J W3=-PΔV=-P3(V3-V1)=101325×(0.0224-0.0448)=2269.68J Q3=ΔU3-W3=-3404.58J-2269.68J=-5674.26J 【4】在 291K 和 100kPa 下,1molZn(s)溶于足量稀盐酸中,置换出 1molH2(g),并放热 152KJ。若以 Zn 和盐酸为系统,求该反应所做的功及系统热力学能的变化。 解 该反应 Zn(s)+2HCl(a)=ZnCl2(s)+H2(g) 所以 ( ) H2 W p V p V V p V = − 外 = 生成物 − 反应物 1mol 8.314J K mol 291K 2.42k J 1 1 = − • • = − − − U = Q +W = −152 − 2.42 = −154.4k J 【5】在 298K 时,有 2molN2(g),始态体积为 15dm3,保持温度不变,经下列三个过程 膨胀到终态体积为 50dm3,计算各过程的 ΔU,ΔH,W 和 Q 的值。设气体为理想气体。 (1)自由膨胀; (2)反抗恒外压 100kPa 膨胀;