
第十一章化学动力学基础(一) 【复习题】 【1】请根据质量作用定律写出下列基元反应的反应速率表示式(试用各种物质分别表示)。 (1)A+B=2P: (2)2A+B=2P: (3)A+2B=P+2S: (4)2CI+M=CL2+M。 【解】 ()万=-4.-dg-1d=AB dtdt 2 dt (2)5=-4=-a=d=A8 2dt dt 2 dt (3)5=-d4-4g-dg-)d的=4B研 dt 2dt dt 2 dt (4)n=-dicn=-dM]_diCl]-diMl=RCIM] 2dt dt dt dt 【2】零级反应是否是基元反应?具有简单级数的反应是否一定是基元反应?反应 Pb(C2H)4一Pb+4C,H是否可能为基元反应? 【解】零级反应不可能是基元反应,具有简单级数的反应不一定是基元反应,反应 Pb(C,H).一Pb+4C,H不是基元反应,因为基元反应分子数即反应物的粒子数没有超 过3的,而且根据微观可逆性原理,一个基元反应的逆反应也是一个基元反应,而该反应的 逆反应的粒子数为5。 【3】在气相反应动力学中,往往可以用压力代替浓度,若aA→P为n级反应,若k。 是以压力表示的反应速率常数,P4是A的分压,所以气体可看作理想气体时,请证明: k。=k.(RT)"。 【解】当用浓度表示时有: dC4=k.C… …① -adt 当用压力表示时有: 迎4=k。p”…② -adt 由②得 dC RT =kp[C RTT -adt 或 aC=k,IC,RTTRT- 与①比较得 -adt k C=k[C RTT RT-
第十一章 化学动力学基础(一) 【复习题】 【1】请根据质量作用定律写出下列基元反应的反应速率表示式(试用各种物质分别表示)。 (1) A B P + 2 ; (2) 2 2 A B P + ; (3) A B P S + + 2 2 ; (4) 2 2CI M CI M + + 。 【解】 (1) 1 [ ] [ ] 1 [ ] [ ][ ] 2 d A d B d P r k A B dt dt dt = − = − = = (2) 2 2 [ ] [ ] 1 [ ] [ ] [ ] 2 2 d A d B d P r k A B dt dt dt = − = − = = (3) 2 3 [ ] [ ] [ ] 1 [ ] [ ][ ] 2 2 d A d B d P d S r k A B dt dt dt dt = − = − = = = (4) 2 2 4 [ ] [ ] [ ] [ ] [ ] [ ] 2 d Cl d M d M d Cl r k Cl M dt dt dt dt = − = − = = = 【2】零级反应是否是基元反应?具有简单级数的反应是否一定是基元反应?反应 ( 2 5 2 5 )4 Pb C H Pb C H + 4 是否可能为基元反应? 【解】零级反应不可能是基元反应,具有简单级数的反应不一定是基元反应,反应 ( 2 5 2 5 )4 Pb C H Pb C H + 4 不是基元反应,因为基元反应分子数即反应物的粒子数没有超 过 3 的,而且根据微观可逆性原理,一个基元反应的逆反应也是一个基元反应,而该反应的 逆反应的粒子数为 5。 【3】在气相反应动力学中,往往可以用压力代替浓度,若 aA P → 为 n 级反应,若 kp 是以压力表示的反应速率常数,pA 是 A 的分压,所以气体可看作理想气体时,请证明: ( ) 1 n p c k k RT − = 。 【解】当用浓度表示时有: A n c A dC k C adt = − …………………………………………① 当用压力表示时有: A n p A dp k p adt = − ……………………………………………② 由②得 [ ] A n p A dC RT k C RT adt = − 或 1 [ ] A n p A dC k C RT RT adt − = − 与①比较得 1 [ ] n n c A p A k C k C RT RT− =

即k。=k.[RT] 【4】对于一级反应,列式表示当反应物反应掉所需要的时间t是多少?试证明一级 n 反应的转化率分别达到50%,75%,87.5%所需的时间分别为,2,32 1, 【解】根据一级反应公式t= 1 In- k1-y 得 =-n- k1-1/nkn-1 当n=50%时 1 1 In2 40-元n1-50% In- 当n=75%时 1_2ln2 175%= k“1-75%k =21p 当n=87.5%时 1 1s75%=左lh 1_3n2-3e k11-87.5%k 【5】对反应A→P,当A反应掉3所需时间为A反应掉1所需时间的3倍,该反应是 4 2 几级反应?若当A反应掉3所需时间为A反应掉1所需时间的5倍,该反应又是几级反应? 请用计算式说明。 【解】用尝试法 对于零级反应 坐=34_3 2V22 1、3 对于一级反应 4 n4-2 In2 In 1☑ 2 3/4 对于二级反应 1×(1-3/4) =3 t 1/2 1×(1-1/2) 1 对于三级反应 塑=-342下 ty2 1■ (1-1/2)2 所以当t4=3t2时该反应为二级反应,当14=5t2时,该反应为三级反应。 【6】某一反应进行完全所需时间是有限的,且等于。(。为反应物起始浓度),则该 k
即 1 [ ] n p c k k RT − = 【4】对于一级反应,列式表示当反应物反应掉 1 n 所需要的时间 t 是多少?试证明一级 反应的转化率分别达到 50%,75%,87.5%所需的时间分别为 12 t , 12 2t , 12 3t 。 【解】 根据一级反应公式 1 1 1 ln 1 t k y = − 得 1 1 1 1 1 1 ln ln 1 1 1 n n t k n k n = = − − 当 n=50%时 1 2 1 1 1 1 ln 2 ln 1 50% t k k = = − 当 n=75%时 75% 1 2 1 1 1 1 2ln 2 ln 2 1 75% t t k k = = = − 当 n=87.5%时 87.5% 1 2 1 1 1 1 3ln 2 ln 3 1 87.5% t t k k = = = − 【5】对反应 A P → ,当 A 反应掉 3 4 所需时间为 A 反应掉 1 2 所需时间的 3 倍,该反应是 几级反应?若当 A 反应掉 3 4 所需时间为 A 反应掉 1 2 所需时间的 5 倍,该反应又是几级反应? 请用计算式说明。 【解】 用尝试法 对于零级反应 3 4 1 2 3 4 3 1 2 2 t t = = 对于一级反应 3 4 1 2 1 ln 3 1 ln 4 4 2 1 ln 2 ln 1 1 2 t t − = = = − 对于二级反应 3 4 1 2 3 4 1 (1 3 4) 3 1 2 1 (1 1 2) t t − = = − 对于三级反应 ( ) ( ) 2 2 3 4 1 2 2 2 1 1 1 3 4 1 5 1 1 1 1 2 1 t t − − = = − − 所以当 3 4 1 2 t t = 3 时该反应为二级反应,当 3 4 1 2 t t = 5 时,该反应为三级反应。 【6】某一反应进行完全所需时间是有限的,且等于 0 c k (c0 为反应物起始浓度),则该
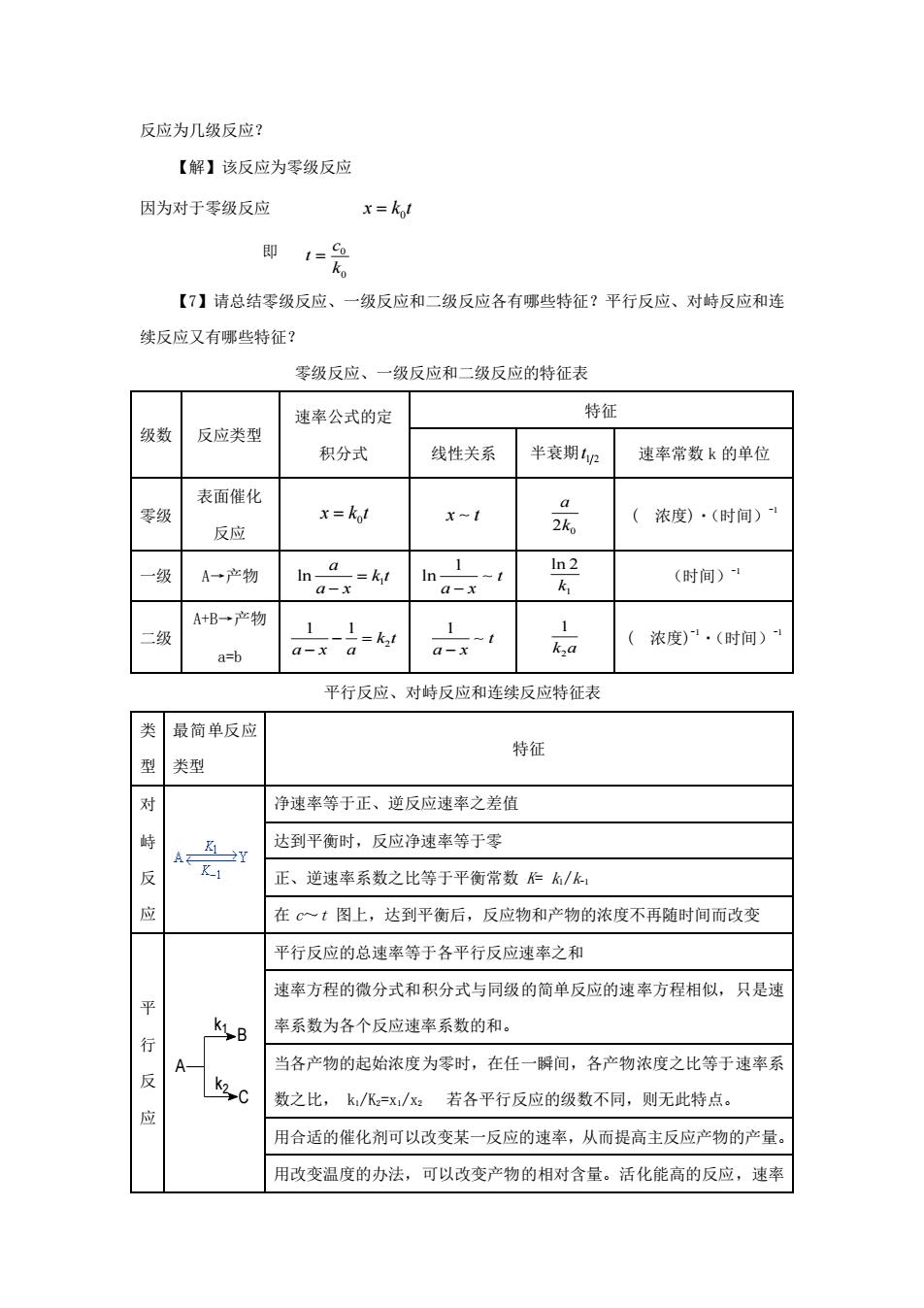
反应为几级反应? 【解】该反应为零级反应 因为对于零级反应 x=kot 即 1= Ko 【7】请总结零级反应、一级反应和二级反应各有哪些特征?平行反应、对峙反应和连 续反应又有哪些特征? 零级反应、一级反应和二级反应的特征表 速率公式的定 特征 级数 反应类型 积分式 线性关系 半衰期t2 速率常数k的单位 表面催化 零级 x=kot x~I 2ko (浓度)·(时间) 反应 级 A→产物 In- a In2 =kt -t k (时间)1 a-x a-x A+B→产物 11 1 二级 a-x a =k21 1 t h ( 浓度)·(时间) a=b a-x 平行反应、对峙反应和连续反应特征表 类 最简单反应 特征 型 类型 对 净速率等于正、逆反应速率之差值 峙 达到平衡时,反应净速率等于零 反 正、逆速率系数之比等于平衡常数仁k/k1 应 在C~t图上,达到平衡后,反应物和产物的浓度不再随时间而改变 平行反应的总速率等于各平行反应速率之和 速率方程的微分式和积分式与同级的简单反应的速率方程相似,只是速 平 行 KiB 率系数为各个反应速率系数的和。 A 当各产物的起始浓度为零时,在任一瞬间,各产物浓度之比等于速率系 反 K2-C 数之比,k/K2=x/x2若各平行反应的级数不同,则无此特点。 应 用合适的催化剂可以改变某一反应的速率,从而提高主反应产物的产量。 用改变温度的办法,可以改变产物的相对含量。活化能高的反应,速率
反应为几级反应? 【解】该反应为零级反应 因为对于零级反应 0 x k t = 即 0 0 c t k = 【7】请总结零级反应、一级反应和二级反应各有哪些特征?平行反应、对峙反应和连 续反应又有哪些特征? 零级反应、一级反应和二级反应的特征表 级数 反应类型 速率公式的定 积分式 特征 线性关系 半衰期 12 t 速率常数 k 的单位 零级 表面催化 反应 0 x k t = x t 2 0 a k ( 浓度)·(时间)-1 一级 A→产物 1 ln a k t a x = − 1 ln t a x − 1 ln 2 k (时间)-1 二级 A+B→产物 a=b 2 1 1 k t a x a − = − 1 t a x − 2 1 k a ( 浓度) -1·(时间)-1 平行反应、对峙反应和连续反应特征表 类 型 最简单反应 类型 特征 对 峙 反 应 净速率等于正、逆反应速率之差值 达到平衡时,反应净速率等于零 正、逆速率系数之比等于平衡常数 K= k1/k-1 在 c~t 图上,达到平衡后,反应物和产物的浓度不再随时间而改变 平 行 反 应 A B C k1 k2 平行反应的总速率等于各平行反应速率之和 速率方程的微分式和积分式与同级的简单反应的速率方程相似,只是速 率系数为各个反应速率系数的和。 当各产物的起始浓度为零时,在任一瞬间,各产物浓度之比等于速率系 数之比, k1/K2=x1/x2 若各平行反应的级数不同,则无此特点。 用合适的催化剂可以改变某一反应的速率,从而提高主反应产物的产量。 用改变温度的办法,可以改变产物的相对含量。活化能高的反应,速率

系数随温度的变化率也大。 生成B的净速率等于生成速率与消耗速率的差值 连 续 当k>k时,第二步反应决定整个反应的速率,当k《k,时,第一步 ABc K 反 反应决定整个反应的速率。 应 中间产物B最大时的时间为 t =Inkg -In k k2-k 【8】某总包反应速率常数k与各基元反应速率常数的关系为k=k 则该反 2k4 应的表观活化能E和指前因子与各基元反应活化能和指前的关系如何? 【解】根据 那么k=Aexp( RT RT RT 代入速率宿数的关系=(条)中府 exp(-E./RT) RT 2A exp(-E/RT) 化简得 A=A 24, .=+ 【9】某定容基元反应的热效应为100kJ·mo1,则该正反应的实验活化能Ea的数值 将大于、等于还是小于100kJ,mo,或是不能确定?如果反应热效应为-100kJ·mo~1,则 Fa的数值又将如何? 【解】若反应的热效应为100kJ·mo厂1,则正反应的实验活化能a的数值将大于 100kJ-mol: 若反应热效应为-100kJ·mol~,则Ea的数值无法确定。 【10】某反应的Ea值为190kJ·mol1,加入催化剂后活化能降为136kJ·mol。设加 入催化剂前后指前因子A值保持不变,则在773K时,加入催化剂后的反应速率是原来的多 少倍?
系数随温度的变化率也大。 连 续 反 应 k1 k2 A B C 生成 B 的净速率等于生成速率与消耗速率的差值 当 1 2 k k 时,第二步反应决定整个反应的速率,当 1 2 k k 时,第一步 反应决定整个反应的速率。 中间产物 B 最大时的时间为 2 1 2 1 ln ln m k k t k k − = − 【8】某总包反应速率常数 k 与各基元反应速率常数的关系为 1 2 1 2 2 4 k k k k = ,则该反 应的表观活化能 Ea 和指前因子与各基元反应活化能和指前的关系如何? 【解】根据 exp( ) E a k A RT − = 那么 ,1 1 1 exp( ) E a k A RT − = , ,2 2 2 exp( ) E a k A RT − = , ,4 4 4 exp( ) E a k A RT − = 代入速率常数的关系 1 2 1 2 2 4 k k k k = 中得 exp( ) E a A RT − = 1 2 ,2 1 ,1 2 4 ,4 exp( ) exp( ) 2 exp( ) a a a E A E RT A RT A E RT − − − 化简得 1 2 1 2 4 2 A A A A = ,2 ,1 ,4 1 1 2 2 E E E E a a a a = + − 【9】某定容基元反应的热效应为 1 100kJ mol − ,则该正反应的实验活化能 Ea 的数值 将大于、等于还是小于 1 100kJ mol − ,或是不能确定?如果反应热效应为 1 100kJ mol − − ,则 Ea 的数值又将如何? 【解】若反应的热效应为 1 100kJ mol − ,则正反应的实验活化能 Ea 的数值将大于 1 100kJ mol − ; 若反应热效应为 1 100kJ mol − − ,则 Ea 的数值无法确定。 【10】某反应的 Ea 值为 1 190kJ mol − ,加入催化剂后活化能降为 1 136kJ mol − 。设加 入催化剂前后指前因子 A 值保持不变,则在 773K 时,加入催化剂后的反应速率是原来的多 少倍?

【解】k=Aexp(E)=Aexp190x10 (k为不加催化剂时的速率常数) RT RT 6=4m营2-4e0 (2为加催化剂时的速率常数) k2 =exp(- 36×103-190×103 =4457.83 8.314×773 即加入催化剂后的反应速率是原来的4457.83倍。 【11】根据vant Hoff经验规则:“温度每增加10K,反应速率增加2~4倍”。在298~ 308K的温度区间内,服从规则的化学反应之活化能值E的范围为多少?为什么有的反应温 度升高,速率反而下降? 【解】 根据公式: -E11 In kR(T 又有 2≤k≤4 k T.TR.In- 所以 k E。2,-T 298×308×8.314×2≤E,≤298×308×8.314×4 308-298 308-298 152.6 kJ-mol-1≤E,≤305.2kJmo厂 温度升高,速率下降的原因可能是高温对催化剂性能有不利的影响。 【12】某温度时,有一气相一级反应A(g)→2B(g)+C(g),在恒温、恒容条件下进行。 设反应开始时,各物质的浓度分别为a,b,c,气体总压力为po,经t时间及当A完全分解时的 总压力分别为p:和P。,试证明该分解反应的速率常数为 k=IInPa-Po t P.-P 证明 A(g) →2B(g)+C(g) t=0 a b Po=(a+b+c)RT (1) t=t a-x b+2x C+x P.=(a+b+c+2x)RT (2) t=00 b+2a c+a P:=(3a+b+c)RT (3) 由(1)、(3)得 a=P。-pa 2RT 由(2)、(3)得 a-x=P。-卫 2RT
【解】 3 ,1 1 190 10 exp( ) exp( ) E a k A A RT RT − − = = (k1为不加催化剂时的速率常数) 3 ,2 2 136 10 exp( ) exp( ) E a k A A RT RT − − = = (k2为加催化剂时的速率常数) 3 3 2 1 136 10 190 10 exp( ) 4457.83 8.314 773 k k − = − = 即加入催化剂后的反应速率是原来的 4457.83 倍。 【11】根据vant Hoff经验规则:“温度每增加10K,反应速率增加2~4倍”。在298~ 308K 的温度区间内,服从规则的化学反应之活化能值 Ea 的范围为多少?为什么有的反应温 度升高,速率反而下降? 【解】 根据公式: 2 1 1 2 1 1 ln E a k k R T T = − 又有 2≤ 2 1 k k ≤4 所以 2 1 2 1 2 1 ln a k T T R k E T T = − 298 308 8.314 2 308 298 − ≤ E a ≤ 298 308 8.314 4 308 298 − 1 152.6kJ mol − ≤ E a ≤ 1 305.2kJ mol − 温度升高,速率下降的原因可能是高温对催化剂性能有不利的影响。 【12】某温度时,有一气相一级反应 A g B g C g ( ) → + 2 ( ) ( ) ,在恒温、恒容条件下进行。 设反应开始时,各物质的浓度分别为 a,b,c,气体总压力为 p0,经 t 时间及当 A 完全分解时的 总压力分别为 pt 和 p ,试证明该分解反应的速率常数为 1 k t = ln 0 t p p p p − − 证明 ( ) ( ) ( ) 0 2 0 ( ) (1) 2 ( 2 ) (2) 0 2 (3 ) (3) t A g B g C g t a b c p a b c RT t t a x b x c x p a b c x RT t b a c a p a b c RT → + = = + + = − + + = + + + = + + = + + 由(1)、(3)得 0 2 p p a RT − = 由(2)、(3)得 2 t p p a x RT − − =

根据一级反应公式: k=IIn-a t a-x P-Po 得: k=in2RT=hnp。-p t"P。-ptPm-pP 2RT 【13】已知平行反应Aa1→B和AB2→C,且E1>E22,为提高B的产量,应 采取什么措施? 【解】可以采取两种措施:(1)选择合适的催化剂:(2)升高温度。 【14】从反应机理推导速率方程时通常有哪几种近似方法?各有什么适用条件? 【解】稳态近似法、平衡假设近似法、速控法等, 稳态近似法适用条件是:反应能迅速达到稳定态,而且中间物浓度比反应物和产物的浓 度小的多,一般这些中间物质是自由基或自由原子。 平衡假设近似法适用条件是:快速的对峙反应 速控法适用条件是:在一系列的反应机理中,若其中有一步反应的速率最慢,那么整个 反应的速率就是该步反应的速率。 例如:总反应为A+B→P的反应机理为: 4之=C C+Bs→P ,-=kC[ B为反应物而C为中间产物 dt 当k,+k[B]≥k时,说明C的浓度很小,而且很容易消耗而难生成,可以对C做稳态近 似法处理g=k[A-kIC]-,[CI[B=0 dt [C]=,1代入速率方程得 k+k[B] c2=kL4[B☐ r= dt k+k[B] 这时,如果k[B之k,中间物大多是形成P而不是分解为A, 则r=k[4川即第一步为速控步 如果k,[B]《k1,中间物大多是形成A而不是分解为P,说明第二步反应很慢,为速 控步,第一步能维持平衡,如果再让k≤k时,第一步很快建立平衡,就可以用平衡假设
根据一级反应公式: 1 1 ln a k t a x = − 得: 0 0 1 1 1 2 ln ln 2 t t p p RT p p k t t p p p p RT − − = = − − 【13】已知平行反应 Ea,1 A B ⎯⎯⎯→ 和 Ea,2 A C ⎯⎯⎯→ ,且 E E a a ,1 ,2 > ,为提高 B 的产量,应 采取什么措施? 【解】可以采取两种措施:(1)选择合适的催化剂;(2)升高温度。 【14】从反应机理推导速率方程时通常有哪几种近似方法?各有什么适用条件? 【解】 稳态近似法、平衡假设近似法、速控法等, 稳态近似法适用条件是:反应能迅速达到稳定态,而且中间物浓度比反应物和产物的浓 度小的多,一般这些中间物质是自由基或自由原子。 平衡假设近似法适用条件是:快速的对峙反应 速控法适用条件是:在一系列的反应机理中,若其中有一步反应的速率最慢,那么整个 反应的速率就是该步反应的速率。 例如:总反应为 A+B→P 的反应机理为: 1 1 k k A C − 2 k C B P + ⎯⎯→ 2 [ ][ ] p dc r k C B dt = = B 为反应物而 C 为中间产物 当 1 2 1 k k B k [ ] − + 时,说明 C 的浓度很小,而且很容易消耗而难生成,可以对 C 做稳态近 似法处理 1 1 2 [ ] [ ] [ ] [ ][ ] 0 d C k A k C k C B dt = − − = − 1 1 2 [ ] [ ] [ ] k A C k k B − = + 代入速率方程得 2 1 1 2 [ ][ ] [ ] p dc k k A B r dt k k B − = = + 这时,如果 2 1 k B k [ ] − 中间物大多是形成 P 而不是分解为 A, 则 1 r k A = [ ] 即第一步为速控步 如果 2 1 k B k [ ] − ,中间物大多是形成 A 而不是分解为 P,说明第二步反应很慢,为速 控步,第一步能维持平衡,如果再让 1 1 k k− 时,第一步很快建立平衡,就可以用平衡假设

法K= k_[C] k1[A] 得[C= k r=- e=kkB] dt k 【习题】 【1】在298K时,N,0,(g)=N,0,(g)+0,(g),该分解反应的半衰期12=5.7h此值与 N,O,(g)的起始浓度无关。试求: (1)该反应的速率常数: (2)N,O,(g)转化掉90%所需的时间。 【解】根据半衰期与反应物的起始浓度无关可知该反应为一级反应, (1)对一级反应半衰期为:=n2 得 k=h2=n2=0.122h 5.7h (2)1=n,1= 1 1 k1-y0.122h-TIn 1-90% =18.87h 【2】某物质A的分解反应为二级反应,当反应进行到A消耗了1/3时,所需时间为2min, 若继续反应掉同样这些量的A,应需多长时间? 【解】 设A的初始浓度为,根据二级反应的公式L= a-x a 有 11 =k2min …(① a-% a 1 1 a-2a7 =k3f…② 3 a 由①②比较得 t=8min 可见还需要6加in的时间 【3】有反应A→P,实验测得是级反应,试证明: D【Ag-4-a: 2a-5-儿a 【证明】(1)假设反应物的起始浓度为[A]
法 1 1 [ ] [ ] c k C K k A − = = 得 1 1 [ ] [ ] k A C k− = 1 2 1 [ ][ ] p dc k k r A B dt k− = = 【习 题】 【1】在 298K 时, 2 5 2 4 2 1 ( ) ( ) ( ) 2 N O g N O g O g + ,该分解反应的半衰期 1 2 t h = 5.7 此值与 N O g 2 5 ( ) 的起始浓度无关。试求: (1)该反应的速率常数; (2) N O g 2 5 ( ) 转化掉 90%所需的时间。 【解】根据半衰期与反应物的起始浓度无关可知该反应为一级反应, (1) 对一级反应半衰期为: 1 2 1 ln 2 t k = 得 1 1 1 2 ln 2 ln 2 0.122 5.7 k h t h − = = = (2) 1 2 1 1 1 1 ln ln 18.87 1 0.122 1 90% t h k y h− = = = − − 【2】某物质 A 的分解反应为二级反应,当反应进行到 A 消耗了 13 时,所需时间为 2min, 若继续反应掉同样这些量的 A,应需多长时间? 【解】 设 A 的初始浓度为 a,根据二级反应的公式 2 1 1 k t a x a − = − 有 2 1 1 2min 3 k a a a − = − ………………………………① 2 1 1 2 3 k t a a a − = − …………………………………………② 由①②比较得 t =8min 可见还需要 6min 的时间 【3】有反应 A P → ,实验测得是 1 2 级反应,试证明: (1) 1 2 1 2 1 2 O A A kt - = ; (2) ( ) 1 2 1 2 0 2 t A 2 1 k = − 【证明】(1)假设反应物的起始浓度为[A]0

d4=k4的 dt 移项进行定积分 4[4 得 a=2d-即【4-4°- 244时4-4= 即 a=6-l4 【4】在298K时,用旋光仪测定蔗糖的转化速率,在不同时间所测得的旋光度α.如下: t/min 0 10 20 40 80 180 300 00 a,/) 6.60 6.17 5.79 5.00 3.71 1.40 -0.24 -1.98 试求该反应的速率常数k值。 【解】蔗糖的水解反应中水是溶剂,大量存在,所以视为准一级反应,反应为: C2H2zO1+H,Om1→C6HO。+C6H2O6 蔗糖 葡萄糖果糖 t=0 a 0 0 1=1 a-x t=000 设蔗糖、果糖、和葡萄糖的旋角与浓度的比例系数分别为C,C2,C。 那么 do=ca () a,=c(a-x)-cx+c3x=ca+(c3-c-c2)x (2) a。=(C3-C2)a (3) 由(1)-(3)得 a-a。=(G1+C2-C3)a (4) 由(2)-(3)得 a,-a。=(C+C2-C3)(a-x) (5) 由(4)/(5)得-=a &-a。a-x 所以 k=hna-lhn凸-a 1a-x t a-d. 以ln(a,-an)对t作图,得一直线,斜率为-k,则k=52×10-3min1
1 2 [ ] [ ] d A k A dt − = 移项进行定积分 0 [ ] 1 [ ] 0 2 [ ] [ ] A t A d A kdt A = − 得 1 1 2 2 0 kt A A 2 [ ] [ ] = − 即 1 2 1 2 0 1 2 A A kt - = (2)当 0 1 2 A A = 时 1 2 1 2 0 0 1 2 2 1 2 A A t k = - 即 ( ) 1 2 1 2 0 2 t A 2 1 k = − 【4】在 298K 时,用旋光仪测定蔗糖的转化速率,在不同时间所测得的旋光度 αt 如下: t min 0 10 20 40 80 180 300 t (°) 6.60 6.17 5.79 5.00 3.71 1.40 -0.24 -1.98 试求该反应的速率常数 k 值。 【解】蔗糖的水解反应中水是溶剂,大量存在,所以视为准一级反应,反应为: [ ] 12 22 11 2 6 12 6 6 12 6 0 0 0 H C H O H O C H O C H O t t x x x t + + ⎯⎯⎯→ + = − = 蔗糖 葡萄糖 果糖 t=0 设蔗糖、果糖、和葡萄糖的旋角与浓度的比例系数分别为 1 2 3 c c c , , 。 那么 0 1 1 2 3 1 3 1 2 3 2 (1) ( ) ( ) (2) ( ) (3) t c a c a x c x c x c a c c c x c c a = = − − + = + − − = − 由(1)-(3)得 0 1 2 3 ( ) c c c a − = + − (4) 由(2)-(3)得 1 2 3 ( )( ) t c c c a x − = + − − (5) 由(4)/(5)得 0 t a a x − = − − 所以 0 1 1 1 ln ln t a k t a x t − = = − − 以 ln( ) t − 对 t 作图,得一直线,斜率为-k,则 3 1 k 5.2 10 min − − =

或用各组数据代入上述积分式,求出k值,然后取平均值。 【5】在298K时,测定乙酸乙酯皂化反应速率。反应开始时,溶液中酯与碱的浓度都为 0.01mol·dm3,每隔一定时间,用标准酸溶液滴定其中的碱含量,实验所得结果如下: t/min 5 7 10 15 21 25 [OH-]/(10-3mol-dm3) 7.40 6.34 5.50 4.64 3.63 2.88 2.54 (1)证明该反应为二级反应,并求出速率常数k值: (2)若酯与碱的浓度都为0.002mol·dm3,试计算该反应完成95%时所需的时间及该反 应的半衰期。 【解】(1)假设该反应为二级反应,则以 对t作图, [OH-] t/min 3 5 7 10 15 21 25 1 [OH-]/mol-dm 135.1 157.7 181.8 215.5 275.5 347.2 393.2 得一直线,说明该反应为二级反应,斜率为k,得 k =11.85mol-.dm3.min- (2)已知,y=kai 1-y 得 1=1xy 1 0.95 ka1-y11.85×0.002min1-0.95 =801.7min 1 1 n-a1.85x0.02mim=42.2min 【6】含有相同物质的量的A,B溶液,等体积混合,发生反应A+B→C,在反应经过 1.0h后,A己消耗了75%:当反应时间为2.0h时,在下列情况下,A还有多少未反应? (1)当该反应对A一级,对B为零级: (2)当对A,B均为一级: (3)当对A,B均为零级。 【解】(1)当该反应对A一级,对B为零级,运用一级反应的公式 k=n1-1n, t1-y1h“1-0.75 当1=2h时,n4- 1-y=6.25%
或用各组数据代入上述积分式,求出 k 值,然后取平均值。 【5】在 298K 时,测定乙酸乙酯皂化反应速率。反应开始时,溶液中酯与碱的浓度都为 3 0.01mol dm− ,每隔一定时间,用标准酸溶液滴定其中的碱含量,实验所得结果如下: t min 3 5 7 10 15 21 25 3 3 [ ] (10 ) OH mol dm − − − 7.40 6.34 5.50 4.64 3.63 2.88 2.54 (1)证明该反应为二级反应,并求出速率常数 k 值; (2)若酯与碱的浓度都为 3 0.002mol dm− ,试计算该反应完成 95%时所需的时间及该反 应的半衰期。 【解】(1)假设该反应为二级反应,则以 1 [ ] OH − 对 t 作图, t min 3 5 7 10 15 21 25 3 1 [ ]/ OH mol dm − − 135.1 157.7 181.8 215.5 275.5 347.2 393.2 得一直线,说明该反应为二级反应,斜率为 k,得 1 3 1 k mol dm 11.85 min − − = (2)已知 1 y kat y = − 得 1 1 1 0.95 1 11.85 0.002min 1 0.95 y t ka y − = = − − =801.7min 1 2 1 1 1 42.2min 11.85 0.002min t ka − = = = 【6】含有相同物质的量的 A,B 溶液,等体积混合,发生反应 A B C + → ,在反应经过 1.0 h 后,A 已消耗了 75%;当反应时间为 2.0 h 时,在下列情况下,A 还有多少未反应? (1)当该反应对 A 一级,对 B 为零级; (2)当对 A,B 均为一级; (3)当对 A,B 均为零级。 【解】 (1)当该反应对 A 一级,对 B 为零级,运用一级反应的公式 1 1 1 1 1 1 ln ln ln 4 1 1 1 0.75 k h t y h − = = = − − 当 t h = 2 时, 1 1 1 ln 4 ln 2 1 h h y − = − 1 6.25% − = y

(2)当对A,B均为一级时,用a=b的二级反应公式 k=x,y=1x075-3 at1-y1h1-0.75a 当t=2h时,3=1xy a 2a 1-y 得1-y=14.3% (3)当对A,B均为零级时,用零级反应的公式 6=7×x=,0w=0.75a 当t=2h时,0.75a=2y 1 y=1.5 得1-y=-0.5 说明A在此时己经反应完, 假设反应完时,所用的时间为t 0.75_1.0 t=1.33h Th t 【7】298K时,Na0H和CHC00CH皂化作用的速率常数k2与Na0H和CH,C00CH皂化作用 的速率常数k的关系为k=2.8k,。试计算在相同的实验条件下,当有90%的CHC00CH被 分解时,CHC00H的分解分数(设碱与酯的浓度均相等)。 【解】根据二级反应(ab)的公式.,=↓×,二 at 1-y k=1x90% 1 y at1-90% at 1-y 190% k=2.8=41-90% 得y=76% at"1-y 【8】设有一n级反应(n≠1)。若反应物的起始浓度为a,证明其半衰期表示式为(式 中k为速率常数): 2-1-1 =(n-)a-k 【证明】 A→P t=0 a 0 t=t a-x x dx =k(a-x)
(2)当对 A,B 均为一级时,用 a=b 的二级反应公式 2 1 1 0.75 3 1 1 1 0.75 y k at y h a = = = − − 当 t h = 2 时, 3 1 2 1 y a a y = − 得 1 14.3% − = y (3)当对 A,B 均为零级时,用零级反应的公式 0 1 1 k x ay a 0.75 t t = = = 当 t h = 2 时, 1 0.75 2 a ay = y =1.5 得 1 0.5 − = − y 说明 A 在此时已经反应完, 假设反应完时,所用的时间为 t 0.75 1.0 1h t = t h =1.33 【7】298K 时,NaOH 和 CH3COOCH3 皂化作用的速率常数 k2 与 NaOH 和 CH3COOC2H5 皂化作用 的速率常数 2 k 的关系为 k2=2.8 2 k 。试计算在相同的实验条件下,当有 90%的 CH3COOCH3 被 分解时,CH3COO2H5 的分解分数(设碱与酯的浓度均相等)。 【解】根据二级反应( a=b)的公式 2 1 1 y k at y = − 2 1 90% 1 90% k at = − 2 1 1 y k at y = − 2 2 1 90% 2.8 1 90% 1 1 k at k y at y − = = − 得 y = 76% 【8】设有一 n 级反应 (n 1) 。若反应物的起始浓度为 a,证明其半衰期表示式为(式 中 k 为速率常数): ( ) 1 1 2 1 2 1 1 n n t n a k − − − = − 【证明】 A P → t=0 a 0 t=t a-x x ( ) dx n k a x dt = −