
第十二章化学动力学基础(二) 【复习题】 【1】简述碰撞理论和过渡态理论所用的模型、基本假设和忧缺点。 【解】碰撞理论 模型:将反应物分子看成无内部结构刚性球体,它们的碰撞完全是弹性碰撞。 基本假设:是反应物分子只有经过碰撞才能发生反应,但并不是所有碰撞分子都能发生 反应,只有当分子的相对碰撞能等于或超过临界能时才能发生反应。 优点:(1)碰撞理论为人们描述了一幅虽然粗造但十分明确的反应图象,在反应速率理 论的发展中起了很大作用:(2)对Arrheinus公式中的指数项,指前因子或阈能提出了较明 确的物理意义,认为指数项相当于有效碰撞分数,指前因子A相当于碰撞频率:(3)解释 了一部分实验事实,理论所计算的速率常数k与较简单的反应实验值相符。 缺点:(1)要从碰撞理论来计算速率常数k,必须要知道临界能E,它本身不能预言 Ee的大小,还需通过Arrheinus公式来求,而Arrheinus公式中的Ea的求得,首先需要从实 验测得k,这就使该理论失去了从理论上预言k的意义,说明该理论为半经验理论:(2)在 该理论中曾假设反应物分子是无内部结构的刚性球体,这种假设过于粗糙,因此只对比较简 单的反应,理论值与实验值符合的较好,但对更多的反应,计算值与实验值有很大的差别。 过渡态理论 模型:描绘出势能面 基本假设:a化学反应不是通过简单的碰撞完成的,分子相遇后,先形成一种过渡态物 种一一活化络合物:b活化络合物很不稳定,一方面与反应物建立动态平衡,另一方面可分 解成产物:c活化络合物分解成产物的步骤是整个反应的决速步:d活化络合物分解的速率 决定与活化络合物的浓度和性质。 优点:a形象地描绘了基元反应进展的过程:b原则上可以从原子结构的光谱数据和势 能面计算宏观的反应速率常数:c对Arrheinus公式的指前因子作了理论说明,认为它与活 化熵有关:d用势能面形象的说明了为什么需要活化能以及反应遵循的能量最低原理。 缺点:引进了平衡假设和速决步假设并不能符合所有的实验事实:b活化络合物的结构 现在还无法从实验上确定,在很大程度上具有猜测性:c计算方法过于复杂,在实际应用 上还存在很大困难,尤其是对于复杂的多原子反应:d绘制势能面有困难,使该理论受到一 定的限制
第十二章 化学动力学基础(二) 【复习题】 【1】简述碰撞理论和过渡态理论所用的模型、基本假设和忧缺点。 【解】碰撞理论 模型:将反应物分子看成无内部结构刚性球体,它们的碰撞完全是弹性碰撞。 基本假设:是反应物分子只有经过碰撞才能发生反应,但并不是所有碰撞分子都能发生 反应,只有当分子的相对碰撞能等于或超过临界能时才能发生反应。 优点:(1)碰撞理论为人们描述了一幅虽然粗造但十分明确的反应图象,在反应速率理 论的发展中起了很大作用;(2)对 Arrheinus 公式中的指数项,指前因子或阈能提出了较明 确的物理意义,认为指数项相当于有效碰撞分数,指前因子 A 相当于碰撞频率;(3)解释 了一部分实验事实,理论所计算的速率常数 k 与较简单的反应实验值相符。 缺点:(1)要从碰撞理论来计算速率常数 k,必须要知道临界能 Ec,它本身不能预言 Ec的大小,还需通过 Arrheinus 公式来求,而 Arrheinus 公式中的 Ea 的求得,首先需要从实 验测得 k,这就使该理论失去了从理论上预言 k 的意义,说明该理论为半经验理论;(2)在 该理论中曾假设反应物分子是无内部结构的刚性球体,这种假设过于粗糙,因此只对比较简 单的反应,理论值与实验值符合的较好,但对更多的反应,计算值与实验值有很大的差别。 过渡态理论 模型:描绘出势能面 基本假设:a 化学反应不是通过简单的碰撞完成的,分子相遇后,先形成一种过渡态物 种——活化络合物;b 活化络合物很不稳定,一方面与反应物建立动态平衡,另一方面可分 解成产物;c 活化络合物分解成产物的步骤是整个反应的决速步;d 活化络合物分解的速率 决定与活化络合物的浓度和性质。 优点: a 形象地描绘了基元反应进展的过程;b 原则上可以从原子结构的光谱数据和势 能面计算宏观的反应速率常数;c 对 Arrheinus 公式的指前因子作了理论说明,认为它与活 化熵有关;d 用势能面形象的说明了为什么需要活化能以及反应遵循的能量最低原理。 缺点:a 引进了平衡假设和速决步假设并不能符合所有的实验事实;b 活化络合物的结构 现在还无法从实验上确定,在很大程度上具有猜测性; c 计算方法过于复杂,在实际应用 上还存在很大困难,尤其是对于复杂的多原子反应;d 绘制势能面有困难,使该理论受到一 定的限制

【2】碰撞理论中的阈能Ec的物理意义是什么?与Arrhenius活化能Ea在数值上有何 关系? 【解】阈能Ec是指两个相互碰撞分子的相对平动能在其质心连线上的分量所必须超过 的最小值。与Ea的关系为:Ea=Ec+1/2RT 【3】碰撞理论中为什么要引入概率因子P,P小于1的主要原因是什么? 【解】碰撞理论中以硬球为模型,忽略了分子的特性,使计算值与实验值有偏差,有时 差别达10”,为此不得不引入概率因子P进行校正,P中包括了降低分子有效碰撞的所有各 种因素。 P小于1的主要原因是分子间的能量传递作用需要一定的时间,能量较低的分子达不到 活化,构成无效碰撞。 【4】有一双分子气相反应A(g)+B(g)→P(g),如用简单碰撞理论计算其指前因子, 所得的数量级约为多少? 【解】如果用简单碰撞理论计算其指前因子所得的数量级约为10?。 【5】过渡态理论中的活化焓△H与Arrhenius活化能E,在物理意义和数值上各有何不 同?如有一气相反应A(g)+BC(g)→AB(g)+C(g),试导出△H与Ea之间的关系。 【解】(1)△H是反应物转变成活化络合物过程中的焓变:而E。是活化络合物的平均 能量与反应的平均能量的差值,他们的关系为:E=△H+RT-△(p)m 对凝聚相反应:E,=△H+RT 对气相反应:E。=AH+(I-∑哈)RT (2)E。=△H-RT 【6】在常温下,过渡态理论中的普适因子k:工的单位是什么?数量级约为多少? h 【解】过渡态理论中的普适因子k:工的单位是s,数量级约为10s 【7】试证明气相基元反应A+B。→2Cg的指前因子为 若气相基元反应为2A(g)→C(g)或A(g)+2B(g)→C(g),A的表示式又将如何?
【2】碰撞理论中的阈能 EC的物理意义是什么?与 Arrhenius 活化能 Ea 在数值上有何 关系? 【解】阈能 EC是指两个相互碰撞分子的相对平动能在其质心连线上的分量所必须超过 的最小值。与 Ea 的关系为: Ea=EC+1/2RT 【3】碰撞理论中为什么要引入概率因子 P,P 小于 1 的主要原因是什么? 【解】碰撞理论中以硬球为模型,忽略了分子的特性,使计算值与实验值有偏差,有时 差别达 10-9,为此不得不引入概率因子 P 进行校正,P 中包括了降低分子有效碰撞的所有各 种因素。 P 小于 1 的主要原因是分子间的能量传递作用需要一定的时间,能量较低的分子达不到 活化,构成无效碰撞。 【4】有一双分子气相反应 A g B g P g ( ) ( ) ( ) + → ,如用简单碰撞理论计算其指前因子, 所得的数量级约为多少? 【解】如果用简单碰撞理论计算其指前因子所得的数量级约为 107。 【5】过渡态理论中的活化焓 r m H 与 Arrhenius 活化能 E a 在物理意义和数值上各有何不 同?如有一气相反应 A g BC g AB g C g ( ) + → + ( ) ( ) ( ) ,试导出 r m H 与 Ea 之间的关系。 【解】(1) r m H 是反应物转变成活化络合物过程中的焓变;而 E a 是活化络合物的平均 能量与反应的平均能量的差值,他们的关系为: ( ) E H RT pV a r m m = + − 对凝聚相反应: E H RT a r m = + 对气相反应 : (1 ) a r m B B E H RT = + − (2) E H RT a r m = − 【6】在常温下,过渡态理论中的普适因子 B k T h 的单位是什么?数量级约为多少? 【解】过渡态理论中的普适因子 B k T h 的单位是 s -1 ,数量级约为 1013 s -1 . 【7】试证明气相基元反应 ( ) ( ) ( ) 2 A B C g g g + → 的指前因子为 ( ) 1 2 exp B r m k T S A e c h R − = 若气相基元反应为 2 A g C g ( ) → ( ) 或 A g B g C g ( ) + → 2 , ( ) ( ) A 的表示式又将如何?

【证明】=k(e),又AGe'=-RTnk.(y]门或=eyep-△Gc2 RT k-发 h exp((exp(() h R RT 与Arhenius公式相对:照A=k。(yecxp(△S),n为所有反应物系数之和,所以 h R 4-7erecmag) R 4-k。(ee2epAS) h R k(ex( h 【8】溶剂对化学反应的速率有哪些影响(包括物理方面和化学方面)?所谓“笼效应” 和“遭遇"”其含义是什么?原盐效应与离子所带电荷及离子强度有何关系?对下面几个反应, 若增加溶液中的离子强度,则其反应速率常数是增大、减少还是不变? (1)NH;+CNO-=CO(NH2 )2 (2)CH,COOC,H,+OH→P (3)S,O2+IΓ→P 【解】(1)物理方面:解离作用、传能作用、介电性质、离子与离子、离子与溶剂分 子间的相互作用等:化学方面:溶剂可以对反应起催化作用、溶剂本身可能参加反应等。具 体表现为:a溶剂的介电常数对有离子参加的反应有影响:b.溶剂的极性对反应速率有影响: c.溶剂化的影响;d离子强度的影响(亦称为原盐效应)。 (2)所谓“笼效应”:就是指反应分子在溶剂分子形成的笼中进行的多次碰撞(或振动), 这种在笼中连续的反复碰撞称为一次遭遇。 (3)1g=2:,B4N,当:B>0时,产生正的原盐效应::4。<0时,产生负的原 盐效应:242B=0时,不产生原盐效应。 (4)对反应(1)二42B=0不产生原盐效应,则反应的速率常数不变:
【 证 明 】 1 ( )n c c k k c − = , 又 1 ( ) [ln ( ) ] n r m c G c RT k c − = − 或 1 ( ) ( ) exp( ) n r m c G c k c RT − = − B c k T k k h = 1 ( ) ( ) ( ) exp( )exp( ) B n n r m r m k T S c H c k c e h R RT − = − 与 Arrhenius 公式相对照: 1 ( ) exp( ) B n n r m k T S A c e h R − = ,n 为所有反应物系数之和,所以 1 2 1 ( ) exp( ) B r m k T S A c e h R − = 1 2 2 ( ) exp( ) B r m k T S A c e h R − = 2 3 3 ( ) exp( ) B r m k T S A c e h R − = 【8】溶剂对化学反应的速率有哪些影响(包括物理方面和化学方面)?所谓“笼效应” 和“遭遇”其含义是什么?原盐效应与离子所带电荷及离子强度有何关系?对下面几个反应, 若增加溶液中的离子强度,则其反应速率常数是增大、减少还是不变? (1) 4 2 2 NH CNO CO NH ( ) + − + = (2) CH COOC H OH P 3 2 5 − + → (3) 2 2 3 S O I P − − + → 【解】(1)物理方面:解离作用、传能作用、介电性质、离子与离子、离子与溶剂分 子间的相互作用等;化学方面:溶剂可以对反应起催化作用、溶剂本身可能参加反应等。具 体表现为:a.溶剂的介电常数对有离子参加的反应有影响;b.溶剂的极性对反应速率有影响; c.溶剂化的影响;d.离子强度的影响(亦称为原盐效应)。 (2)所谓“笼效应”:就是指反应分子在溶剂分子形成的笼中进行的多次碰撞(或振动), 这种在笼中连续的反复碰撞称为一次遭遇。 (3) 0 lg 2 A B k z z A I k = ,当 A B z z >0 时,产生正的原盐效应; A B z z <0 时,产生负的原 盐效应; A B z z =0 时,不产生原盐效应。 (4)对反应(1) A B z z =0 不产生原盐效应,则反应的速率常数不变;

对反应(2)二4B0产生正的原盐效应,则速率常数增大: 【9】常用的测试快速反应的方法有哪些?用驰豫法测定快速反应的速率常数,实验中 主要是测定什么数据?驰豫时间的含义是什么?请推导对峙反应 A(8)+B(8)之一G(8)+H(8)的驰豫时间T与k,k,之间的关系。 【解】(1)常用的测试快速反应的方法有驰豫法和闪光光解法。 (2)实验中主要是测定弛豫时间和平衡浓度: (3)驰豫时间π,就是当反应物的浓度距平衡浓度的偏离值△x达到微扰起始时的最大偏 离值△x。的37%时所需要的时间。 (4) A(g)+B(g)G(g)+H(g) =0 b 0 0 tt a-X b-x X t=t(平衡)a-xeb-xe xe xe =k(a-xb-x)-kr dt 并且k,(a-x)b-x)=k2x2 (2) 设△x=x-x。 =dAx=k(a-Ax-x.)(b-Ax-x,)-kj(Ax+x.) 再将(2)式代入得:d=-Ark(a+b-Ar-2x)+k,(Ax+2x,】 dt △x相对很小,所以上式可得:dA=-Ak,(a+b-2x)+k2x】 d dAx=-[k:(a+b-2x.)+k:2x.ldi △x 两边定积分得:nA=[k,(a+b-2x)+k,2x Ax L=k2(a+b-2x)+k22x,=kAL+[B].)+k(G:+[H,) 【10】化学反应动力学分为总包反应、基元反应和态一态反应三个层次,何谓态一态反 应?它与宏观反应动力学的主要区别是什么?当前研究分子反应动态学的主要实验方法有 哪几种?
对反应(2) A B z z <0 产生负的原盐效应,则速率常数减小; 对反应(3) A B z z >0 产生正的原盐效应,则速率常数增大; 【9】常用的测试快速反应的方法有哪些?用驰豫法测定快速反应的速率常数,实验中 主 要是测定什么数据?驰豫时间的含义是什么?请推导对峙反应 ( ) ( ) ( ) ( ) 2 2 k k A g B g G g H g − + + 的驰豫时间τ与 2 2 k k, − 之间的关系。 【解】(1)常用的测试快速反应的方法有驰豫法和闪光光解法。 (2)实验中主要是测定弛豫时间和平衡浓度; (3)驰豫时间 ,就是当反应物的浓度距平衡浓度的偏离值 x 达到微扰起始时的最大偏 离值 0 x 的 37%时所需要的时间。 (4) ( ) ( ) ( ) ( ) 2 2 k k A g B g G g H g − + + t=0 a b 0 0 t=t a-x b-x x x t=t(平衡) a-xe b-xe xe xe 2 2 2 ( )( ) dx k a x b x k x dt = − − − − ………………………………………………(1) 并且 2 2 2 ( )( ) e e e k a x b x k x − − = − ……………………………………………(2) 设 e = − x x x 2 2 2 ( )( ) ( ) e e e dx d x k a x x b x x k x x dt dt − = = − − − − − + 再将(2)式代入得 : 2 2 [ ( 2 ) ( 2 )] e e d x x k a b x x k x x dt − = − + − − + + x 相对很小,所以上式可得: 2 2 [ ( 2 ) 2 ] e e d x x k a b x k x dt − = − + − + 2 2 [ ( 2 ) 2 ] e e d x k a b x k x dt x − = − + − + 两边定积分得: 0 2 2 ln [ ( 2 ) 2 ] e e x k a b x k x t x − = + − + 2 2 2 2 1 ( 2 ) 2 ([ ] [ ] ) ([ ] [ ] ) e e e e e e k a b x k x k A B k G H = + − + = + + + − − 【10】化学反应动力学分为总包反应、基元反应和态—态反应三个层次,何谓态—态反 应?它与宏观反应动力学的主要区别是什么?当前研究分子反应动态学的主要实验方法有 哪几种?

【解】态一态反应是从微观的角度,观察具有确定量子态的反应物分子经过一次碰撞变 成确定量子态的生成物分子时,整个过程的反应特征。 态一态反应与宏观反应动力学的主要区别是:宏观反应动力学所研究的反应体系中包含 的分子仍是大量的(104个的数量级),无法辨认分子的单次碰撞,也无法区别分子不同能 态的反应物分子的性能,而态-态反应是研究真正的分子水平上的单个分子的碰撞行为。 当前研究分子反应动态学的主要实验方法有:交叉分子束、红外化学发光、和激光诱导 荧光三种。 【11】何谓通-速-角等高图?在质心坐标系中,相对于入射分子束的方向,产物分子散 射的角度分布有哪几种基本类型?从产物的角度分布可获得哪些关于微观反应的信息。 【解】通-速-角等高图是以质心为原点,入射方向为横坐标,对所有的反应作出相应 的标记点,然后将产物密度相等的点用一条线连接起来,即得到通速-角等高图。 相对于入射分子而言,产物分子的散射方向有向前、向后(这两种叫各向异性散射)和 向前后对称(各向同性散射)三种类型。 在通速-角等高图中,对分子散射方向(各向异性、各向同向)、能量分布(动能与内 部运动能)等提供了最直观的信息,对于过渡态够型、寿命及反应模式均能作出明确的结论, 而这些在实验室坐标系中不能得到。 【12】通过交叉分子束实验可研究态-态反应,其装置主要由哪几部分组成?何谓红外 化学发光和激光诱导荧光?它们在化学反应动力学的研究中有何作用? 【解】装置主要有:束源、速度选择器、散射室、检测器和产物速度分子器等: 红外化学发光:是当处于振动、转动激发态的化学反应产物向低能态跃迁时发出的辐射, 记录分析这些光谱,可得到初生成物在振动、转动上的分布。 激光诱导荧光:是用一束可调激光,将初生产物分子、电子从处于某振转态的基态激发 到高电子态的某一振转能级,并检测高电子态发出的荧光,可以确定产物分子在振动能级上 的初始分布情况。 【13】何谓受激单重态和三重态?荧光与磷光有何异同?电子激发态和能量衰减通常有 多少种方式? 【解】当电子被激发时,(1)激发S态中的两电子自旋反平行,仍属$态,被称为单重 态:(2)当激发电子为自旋平行时,由于电子的总自旋角动量在磁场方向可以有三个不同的 分量,故称为激发三重态。当激发分子从激发单重态S1上的某一能态跃迁到基态$0上的 某一能态时所发射的辐射称为荧光:当激发分子从T1态跃迁到$0态时,所发射的辐射称
【解】态—态反应是从微观的角度,观察具有确定量子态的反应物分子经过一次碰撞变 成确定量子态的生成物分子时,整个过程的反应特征。 态—态反应与宏观反应动力学的主要区别是:宏观反应动力学所研究的反应体系中包含 的分子仍是大量的(1024 个的数量级),无法辨认分子的单次碰撞,也无法区别分子不同能 态的反应物分子的性能,而态-态反应是研究真正的分子水平上的单个分子的碰撞行为。 当前研究分子反应动态学的主要实验方法有:交叉分子束、红外化学发光、和激光诱导 荧光三种。 【11】何谓通-速-角等高图?在质心坐标系中,相对于入射分子束的方向,产物分子散 射的角度分布有哪几种基本类型?从产物的角度分布可获得哪些关于微观反应的信息。 【解】 通-速-角等高图是以质心为原点,入射方向为横坐标,对所有的反应作出相应 的标记点,然后将产物密度相等的点用一条线连接起来,即得到通-速-角等高图。 相对于入射分子而言,产物分子的散射方向有向前、向后(这两种叫各向异性散射)和 向前后对称(各向同性散射)三种类型。 在通-速-角等高图中,对分子散射方向(各向异性、各向同向)、能量分布(动能与内 部运动能)等提供了最直观的信息,对于过渡态够型、寿命及反应模式均能作出明确的结论, 而这些在实验室坐标系中不能得到。 【12】通过交叉分子束实验可研究态-态反应,其装置主要由哪几部分组成?何谓红外 化学发光和激光诱导荧光?它们在化学反应动力学的研究中有何作用? 【解】装置主要有:束源、速度选择器、散射室、检测器和产物速度分子器等; 红外化学发光:是当处于振动、转动激发态的化学反应产物向低能态跃迁时发出的辐射, 记录分析这些光谱,可得到初生成物在振动、转动上的分布。 激光诱导荧光:是用一束可调激光,将初生产物分子、电子从处于某振转态的基态激发 到高电子态的某一振转能级,并检测高电子态发出的荧光,可以确定产物分子在振动能级上 的初始分布情况。 【13】何谓受激单重态和三重态?荧光与磷光有何异同?电子激发态和能量衰减通常有 多少种方式? 【解】当电子被激发时,(1)激发 S 态中的两电子自旋反平行,仍属 S 态,被称为单重 态;(2)当激发电子为自旋平行时,由于电子的总自旋角动量在磁场方向可以有三个不同的 分量,故称为激发三重态。当激发分子从激发单重态 S1 上的某一能态跃迁到基态 S0 上的 某一能态时所发射的辐射称为荧光;当激发分子从 T1 态跃迁到 S0 态时,所发射的辐射称
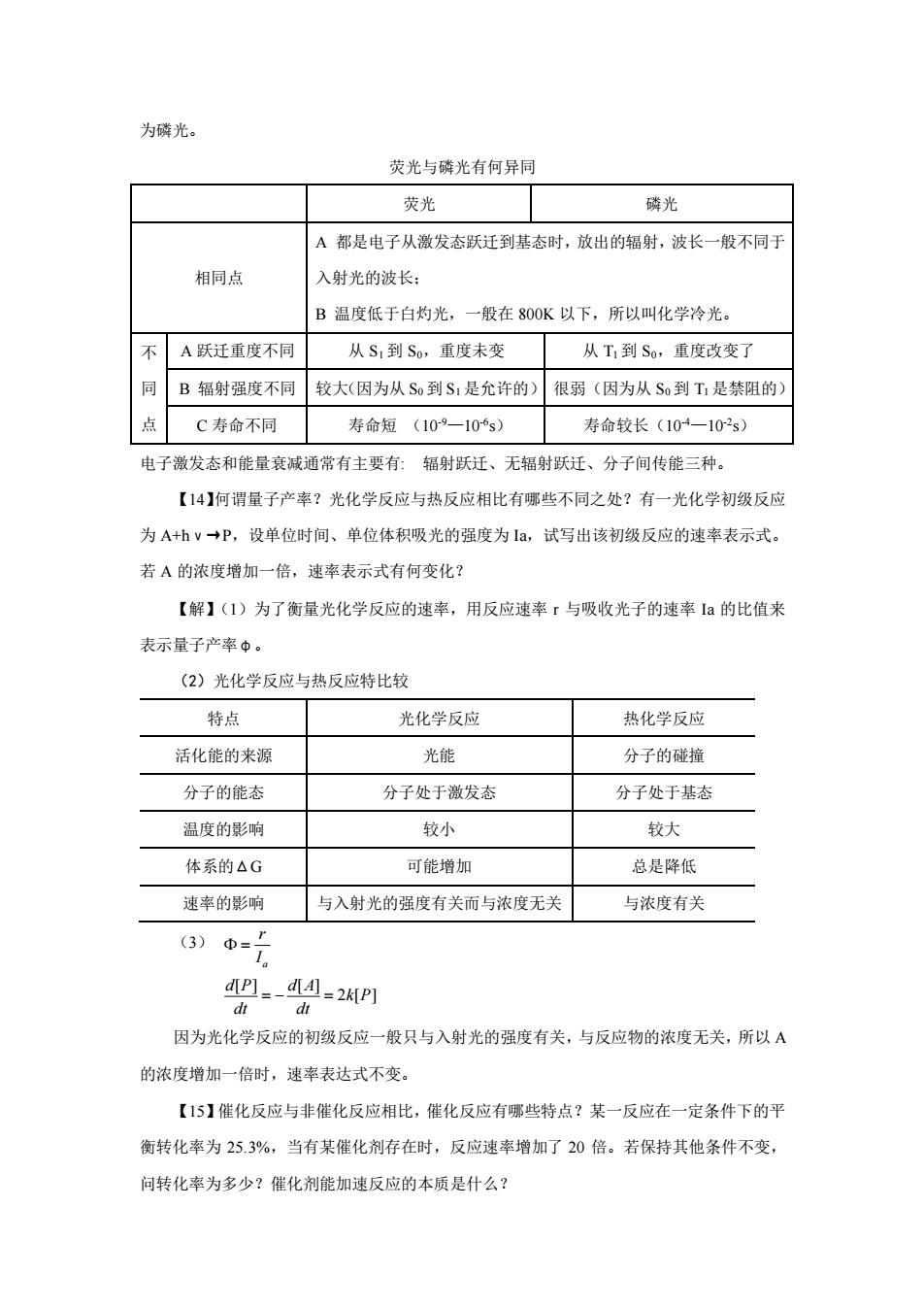
为磷光。 荧光与磷光有何异同 荧光 磷光 A都是电子从激发态跃迁到基态时,放出的辐射,波长一般不同于 相同点 入射光的波长: B温度低于白灼光,一般在800K以下,所以叫化学冷光。 不 A跃迁重度不同 从S1到S,重度未变 从T1到S。,重度改变了 同 B辐射强度不同 较大(因为从S到S1是允许的) 很弱(因为从S到T1是禁阻的) 点 C寿命不同 寿命短(109一106s) 寿命较长(104一102s) 电子激发态和能量衰减通常有主要有:辐射跃迁、无辐射跃迁、分子间传能三种。 【14】何谓量子产率?光化学反应与热反应相比有哪些不同之处?有一光化学初级反应 为A+hv→P,设单位时间、单位体积吸光的强度为Ia,试写出该初级反应的速率表示式。 若A的浓度增加一倍,速率表示式有何变化? 【解】(1)为了衡量光化学反应的速率,用反应速率r与吸收光子的速率Ia的比值来 表示量子产率中。 (2)光化学反应与热反应特比较 特点 光化学反应 热化学反应 活化能的来源 光能 分子的碰撞 分子的能态 分子处于激发态 分子处于基态 温度的影响 较小 较大 体系的△G 可能增加 总是降低 速率的影响 与入射光的强度有关而与浓度无关 与浓度有关 (3) dP]=-d4-2KIP] d dt 因为光化学反应的初级反应一般只与入射光的强度有关,与反应物的浓度无关,所以A 的浓度增加一倍时,速率表达式不变。 【15】催化反应与非催化反应相比,催化反应有哪些特点?某一反应在一定条件下的平 衡转化率为25.3%,当有某催化剂存在时,反应速率增加了20倍。若保持其他条件不变, 问转化率为多少?催化剂能加速反应的本质是什么?
为磷光。 荧光与磷光有何异同 荧光 磷光 相同点 A 都是电子从激发态跃迁到基态时,放出的辐射,波长一般不同于 入射光的波长; B 温度低于白灼光,一般在 800K 以下,所以叫化学冷光。 不 同 点 A 跃迁重度不同 从 S1 到 S0,重度未变 从 T1 到 S0,重度改变了 B 辐射强度不同 较大(因为从 S0 到 S1 是允许的) 很弱(因为从 S0 到 T1 是禁阻的) C 寿命不同 寿命短 (10-9—10-6 s) 寿命较长(10-4—10-2 s) 电子激发态和能量衰减通常有主要有: 辐射跃迁、无辐射跃迁、分子间传能三种。 【14】何谓量子产率?光化学反应与热反应相比有哪些不同之处?有一光化学初级反应 为 A+hν→P,设单位时间、单位体积吸光的强度为 Ia,试写出该初级反应的速率表示式。 若 A 的浓度增加一倍,速率表示式有何变化? 【解】(1)为了衡量光化学反应的速率,用反应速率 r 与吸收光子的速率 Ia 的比值来 表示量子产率φ。 (2)光化学反应与热反应特比较 特点 光化学反应 热化学反应 活化能的来源 光能 分子的碰撞 分子的能态 分子处于激发态 分子处于基态 温度的影响 较小 较大 体系的ΔG 可能增加 总是降低 速率的影响 与入射光的强度有关而与浓度无关 与浓度有关 (3) a r I =[ ] [ ] 2 [ ] d P d A k P dt dt = − = 因为光化学反应的初级反应一般只与入射光的强度有关,与反应物的浓度无关,所以 A 的浓度增加一倍时,速率表达式不变。 【15】催化反应与非催化反应相比,催化反应有哪些特点?某一反应在一定条件下的平 衡转化率为 25.3%,当有某催化剂存在时,反应速率增加了 20 倍。若保持其他条件不变, 问转化率为多少?催化剂能加速反应的本质是什么?

【解】(1)非催化反应要克服一个活化能较大的能峰,而催化反应的反应途径改变,只 需要克服两个较小的能峰。 (2)催化剂既催化正反应,同时也能催化逆反应,所以催化剂只能缩短平衡时间,而 不能改变平衡的组成,故催化剂存在时转化率仍为25.3%。 (3)催化剂能加速反应的本质是改变了反应的历程,降低了表观活化能。 【16】溴和丙酮在水溶液中发生如下反应: CH,COCH (aq)+Br (aq)->CH;COCH,Br(aq)+HBr(aq) 实验得出的动力学方程对Br,为零级,所以说反应中B,起了催化剂作用。这种说法对不对? 为什么?如何解释这样的实验事实。 【解】这种说法不对。 因为催化剂在反应前后,化学性质没有改变,但在反应中与反应物生成某种不稳定的中 间化合物,并且催化剂比影响化学平衡。 实验得出的动力学方程对Br,为零级是由于反应历程中决定速率的那步反应中无B,参 加。 【17】简述酶催化反应的一般历程、动力学处理方法和特点。 Michaelis-Menten Briggs Haldane Heniy等人提出酶催化反应的一般历程为: S+E=ES&→E+P k 动力学处理方法是用稳态近似法处理[E$] dES]=k[S]LE]-k.[ES]-k.[ES]=0 dt 得 [ES]=[S]E] k1+k2 r=k[ES]=k[SIE]-[SIIE] k1+k2 ky 特点:A高度的专一性(高度的选择性):B高度的催化活性(高效率):C反应条件 温和:D反应历程复杂。 【18】何谓自催化反应和化学振荡?化学振荡反应的发生有哪几个必要条件?振荡反应 有何特点? 【解】自催化反应是在给定的条件下的反应体系,反应开始后逐渐形成并积累了某种产 物或中间体(如自由基),这些产物具有催化功能,使反应经过一段诱导期后出现反应大大 加速的现象
【解】(1)非催化反应要克服一个活化能较大的能峰,而催化反应的反应途径改变,只 需要克服两个较小的能峰。 (2)催化剂既催化正反应,同时也能催化逆反应,所以催化剂只能缩短平衡时间,而 不能改变平衡的组成,,故催化剂存在时转化率仍为 25.3%。 (3)催化剂能加速反应的本质是改变了反应的历程,降低了表观活化能。 【16】溴和丙酮在水溶液中发生如下反应: 3 3 2 3 2 CH COCH aq Br aq CH COCH Br aq HBr aq ( ) ( ) ( ) ( ) + → + 实验得出的动力学方程对 Br2 为零级,所以说反应中 Br2 起了催化剂作用。这种说法对不对? 为什么?如何解释这样的实验事实。 【解】这种说法不对。 因为催化剂在反应前后,化学性质没有改变,但在反应中与反应物生成某种不稳定的中 间化合物,并且催化剂比影响化学平衡。 实验得出的动力学方程对 Br2 为零级是由于反应历程中决定速率的那步反应中无 Br2 参 加。 【17】简述酶催化反应的一般历程、动力学处理方法和特点。 Michaelis-Menten Briggs Haldane Heniy 等人提出酶催化反应的一般历程为: 1 2 1 k k k S E ES E P − + ⎯⎯→ + 动力学处理方法是用稳态近似法处理[ES] 1 1 2 [ ] [ ][ ] [ ] [ ] 0 d ES k S E k ES k ES dt = − − = − 得 1 1 2 [ ][ ] [ ] k S E ES k k − = + 2 1 2 2 1 2 [ ][ ] [ ] [ ][ ] M k k S E k r k ES S E k k k − = = = + 特点:A 高度的专一性(高度的选择性);B 高度的催化活性(高效率);C 反应条件 温和;D 反应历程复杂。 【18】何谓自催化反应和化学振荡?化学振荡反应的发生有哪几个必要条件?振荡反应 有何特点? 【解】自催化反应是在给定的条件下的反应体系,反应开始后逐渐形成并积累了某种产 物或中间体(如自由基),这些产物具有催化功能,使反应经过一段诱导期后出现反应大大 加速的现象

化学振荡是有些自催化反应有可能使反应使反应体系中某些物质的浓度随时间或空间 发生周期性的变化的现象。 化学振荡反应的发生的条件必须满足:(1)反应必须是敞开体系且远离平衡态:(2)反 应历程中应包含有自催化的步骤:(3)体系必须有两个稳态存在,即具有双稳定性。 振荡反应特点:反应体系中某些物质的浓度随时间或空间发生周期性的变化,其终态不 是平衡态。 【习题】 【1】在300K时,将1.0g02(g)和0.1gH(g)在1.0dm3的容器内混合,试计算每秒钟、 每单位体积内分子碰撞的总数?设O,(g)和H,(g)为硬球分子,其直径分别为0.339m和 0.247mm。 【解】d6-+d-0339+0.247 ×10-9m=2.93×10-10m 2 2 u=M,42=32x2016=1.897×10 Skg-mol- M,+Mg32+2.016 点-发x602x10 =1.881×102m3 1×10-3 2.h016*62x10 1×109 =2.986×10泸m3 所以 No:Nia 8RT =2.77×1035m3.5- 【2】请计算恒容下,温度每增加10K时, (1)碰撞频率增加的百分数: (2)碰撞时在分子连心线上的相对平动能超过E。=80kJ●mo1的活化分子对的增加百分 数: (3)由上述计算结果可得出什么结论? 8RT 【解】(1)根据Z。=πd广V、 得 InZo=In4+LInT 两端微分得 ZAB 2T 假设反应在450K下进行,则亿丝=10 2w2×450=1.1%
化学振荡是有些自催化反应有可能使反应使反应体系中某些物质的浓度随时间或空间 发生周期性的变化的现象。 化学振荡反应的发生的条件必须满足:(1)反应必须是敞开体系且远离平衡态;(2)反 应历程中应包含有自催化的步骤;(3)体系必须有两个稳态存在,即具有双稳定性。 振荡反应特点:反应体系中某些物质的浓度随时间或空间发生周期性的变化,其终态不 是平衡态。 【习题】 【1】在 300K 时,将 1.0gO2(g)和 0.1gH2(g)在 1.0dm3 的容器内混合,试计算每秒钟、 每单位体积内分子碰撞的总数?设 2 O g( ) 和 2 H g( ) 为硬球分子,其直径分别为 0.339nm 和 0.247nm。 【解】 0.339 0.247 9 10 10 2.93 10 2 2 A B AB d d d m m + + − − = = = 32 2.016 3 1 1.897 10 32 2.016 A B A B M M kg mol M M − − = = = + + 2 23 25 3 3 1 6.02 10 32 1.881 10 1 10 NO m V − − = = 2 23 25 3 3 0.1 6.02 10 2.016 2.986 10 1 10 NH m V − − = = 所以 2 35 3 1 2 2 8 2.77 10 O H AB AB N N RT Z d m s V V − − = = 【2】请计算恒容下,温度每增加 10K 时, (1)碰撞频率增加的百分数; (2)碰撞时在分子连心线上的相对平动能超过 1 80 E kJ mol c − = • 的活化分子对的增加百分 数; (3)由上述计算结果可得出什么结论? 【解】(1)根据 2 8 A B AB AB N N RT Z d V V = 得 1 ln ln ln 2 Z A T AB = + 两端微分得 2 AB AB dZ dT Z T = 假设反应在 450K 下进行,则 10 1.1% 2 450 AB AB dZ Z = =

(2)根据 q-exp) Ing=- Ec RT RT 两端微分得 同样假设反应在450K下进行,则 dg_80×103 J.mol-×10K 98.314Kmo1Fx450K=47.52% (3)由上计算可见:当温度升高10K时,由于分子运动动能的增大,使得活化分子的比例 增高近50%,而分子之间的碰撞频率只增加了1%,两着相差很大,正因为碰撞分子数对温 度的变化不敏感,所以在Arrhenius公式中的指前因子通常被看为常数。 【3】300K时,A和B反应的速率常数为k=1.18×10(molcm3)s,反应活化能 E。=40 kJ.mol-。 (1)用简单碰撞理论估算,具有足够能量能引起反应的碰撞数占总碰撞数的比例? (2)估算反应的概率因子的值? 已知A和B分子的直径分别为0.3nm和0.4nm,假定A和B的相对分子质量都为50。 【解】(1)根据E。=E+RT得 E.=6,-R7=40x102-×8314x30=3875x10'Jmar exp)10 8.314×300 (2)da=+d-03+04x10m=35×100m 2 2 MMB=50×50 u= M+Mg50+50 =25gmol A=πdL 8RT =3.14×3.5×100)2×6.02×102、 /8×8.314×300×2.718 3.14×25×10-3 =1.925×10(molm3)s k=4e是 得:p= 1.18×103(mol.cm)s Ae吾1925x10(molm 40x103j.mo1
(2)根据 exp( ) EC q RT − = ln EC q RT = − 两端微分得 2 dq EC dT q RT = 同样假设反应在 450K 下进行,则 3 1 1 1 2 2 80 10 10 47.52% 8.314 450 dq J mol K q J K mol K − − − = = (3)由上计算可见:当温度升高 10K 时,由于分子运动动能的增大,使得活化分子的比例 增高近 50%,而分子之间的碰撞频率只增加了 1%,两着相差很大,正因为碰撞分子数对温 度的变化不敏感,所以在 Arrhenius 公式中的指前因子通常被看为常数。 【3】300K 时,A 和 B 反应的速率常数为 ( ) 1 5 3 1 k mol cm s 1.18 10 − − − = ,反应活化能 1 40 E kJ mol a − = 。 (1)用简单碰撞理论估算,具有足够能量能引起反应的碰撞数占总碰撞数的比例? (2)估算反应的概率因子的值? 已知 A 和 B 分子的直径分别为 0.3nm 和 0.4nm,假定 A 和 B 的相对分子质量都为 50。 【解】(1)根据 1 2 E E RT a c = + 得 1 1 3 4 1 40 10 8.314 300 3.875 10 2 2 E E RT J mol c a − = − = − = 4 3.875 10 7 exp( ) exp( ) 1.788 10 8.314 300 EC q RT − − − = = = (2) 0.3 0.4 9 10 10 3.5 10 2 2 A B AB d d d m m + + − − = = = 50 50 1 25 50 50 A B A B M M g mol M M − = = = + + 2 8 AB RT A d L = ( ) 2 10 23 3 8 8.314 300 2.718 3.14 3.5 10 6.02 10 3.14 25 10 − − = ( ) 1 8 3 1 1.925 10 mol m s − − − = Ea RT k p A e − = 得: ( ) ( ) 3 1 1 1 1 5 3 1 40 10 1 8 3 1 8.314 300 1.18 10 1.925 10 Ea J mol RT J mol K K k mol cm s p A e mol m s e − − − − − − − − − − − = =

p=5.65×10-3 【4】已知乙炔气体的热分解是二级反应,发生反应的临界能E。=190.4Kgm0,分子 直径为0.5nm,试计算: (1)800K,100kPa时,单位时间、单位体积内的碰撞数: (2)求上述反应条件下的速率常数: (3)求上述反应条件下的初始反应速率。 【解】(1)dM=d4=0.5×10°m M4=2.8×10-2kgmo 。100×103 4=号-8m =15.23mol.m-3 所以Zu=2πdLLA6 RT πM =2×3.14×(0.5×10-y×(6.02×1022×15.232 8.314×800 3.14×2.6×102 =3.77×1034m3.s1 (2)k=2πd4 π -exp() R RT =2×3.14×(0.5×10-9)2×6.02×1023 8.314×800 190.4×103 /3.14x2.6x10Fexp(- 8.314×800 =9.96×10-5molr.m3.s (3)r=LA了 =9.96×10-mo-l.m2.s-l×(15.23molm3)2 =2.31×10-2molm3.s 【5】有基元反应CI(g)+H,(g)→HCI(g)+H(g),己知它们的摩尔质量和直径分别为: Ma=35.45gmol,M4,=2.016gmol-,da=0.20m,du=0.15m (1)请根据碰撞理论计算该反应的指前因子A(令T=350K):
3 p 5.65 10− = 【4】已知乙炔气体的热分解是二级反应,发生反应的临界能 1 190.4 , E kg mol c − = 分子 直径为 0.5nm,试计算: (1)800K,100kPa 时,单位时间、单位体积内的碰撞数; (2)求上述反应条件下的速率常数; (3)求上述反应条件下的初始反应速率。 【解】(1) 9 0.5 10 AA A d d m− = = 2 1 2.8 10 M kg mol A − − = 3 3 0 100 10 [ ] 15.23 8.314 800 p A mol m RT − = = = 所以 2 2 2 0 2 [ ] AA AA A RT Z d L A M = ( ) 2 9 2 23 2 2 8.314 800 2 3.14 (0.5 10 ) 6.02 10 (15.23) 3.14 2.6 10 − − = 34 3 1 3.77 10 m s − − = (2) 2 2 exp( ) c AA A RT E k d M RT − = 3 9 2 23 2 8.314 800 190.4 10 2 3.14 (0.5 10 ) 6.02 10 exp( ) 3.14 2.6 10 8.314 800 − − = − 5 1 3 1 9.96 10 mol m s − − − = (3) 2 0 r k A = [ ] 5 1 3 1 3 2 9.96 10 (15.23 ) mol m s mol m − − − − = 2 3 1 2.31 10 mol m s − − − = 【5】有基元反应 CI g H g HCI g H g ( ) + → + 2 ( ) ( ) ( ), 已知它们的摩尔质量和直径分别为: 2 2 1 1 35.45 , 2.016 , 0.20 , 0.15 M g mol M g mol d nm d nm CI H CI H − − = = = = . (1) 请根据碰撞理论计算该反应的指前因子 A(令 T=350K);