
第2课时杠杆的种类及其应用 素能演练提升 【能力提升】 1悬挂重力大小为G的物体的轻质杠杆,在力的作用下倾斜静止在如图所示的位置。若力施 加在A点,最小的力为FA,若力施加在B点或C点,最小的力分别为FB、Fc,且AB=BO=OC。 下列判断正确的是() G A.F>G B.Fg=G C.FCFC 2.撬棒是人们在劳动中应用杠杆原理的工具。右图是工人利用撬棒撬动大石头的情景,撬棒上 O点为杠杆的支点。下列分析正确的是() A.此时撬棒为等臂杠杆 B.应用此撬棒的主要目的是省力 C.力F的作用点靠近O点会更省力 D.应用此撬棒的主要目的是省距离 3.《墨经》最早记述了秤的杠杆原理。右图中“标“本”表示力臂,“权重”表示力。下列说法 符合杠杆平衡原理的是() 提纽 00 B 标 A.“权”小于“重时,A端一定上扬 B.“权”小于“重时,“标”一定小于“本” C增大“重”时,应把权”向A端移 D.增大“重时,应换用更小的权” 4.(2022贵州毕节中考)下图是常用的一些工具,它给我们带来了很多便利。其中属于费力杠杆 的是() A核桃夹 B.食品夹 C.园艺剪刀 D.天平 5.如图所示,杠杆AOB能绕O点转动。在A点挂一重物G,为使杠杆保持平衡且用力最小,在
第 2 课时 杠杆的种类及其应用 素能演练提升 【能力提升】 1.悬挂重力大小为 G 的物体的轻质杠杆,在力的作用下倾斜静止在如图所示的位置。若力施 加在 A 点,最小的力为 FA;若力施加在 B 点或 C 点,最小的力分别为 FB、FC,且 AB=BO=OC。 下列判断正确的是( ) A.FA>G B.FB=G C.FCFC 2.撬棒是人们在劳动中应用杠杆原理的工具。右图是工人利用撬棒撬动大石头的情景,撬棒上 O 点为杠杆的支点。下列分析正确的是( ) A.此时撬棒为等臂杠杆 B.应用此撬棒的主要目的是省力 C.力 F 的作用点靠近 O 点会更省力 D.应用此撬棒的主要目的是省距离 3.《墨经》最早记述了秤的杠杆原理。右图中“标”“本”表示力臂,“权”“重”表示力。下列说法 符合杠杆平衡原理的是( ) A.“权”小于“重”时,A 端一定上扬 B.“权”小于“重”时,“标”一定小于“本” C.增大“重”时,应把“权”向 A 端移 D.增大“重”时,应换用更小的“权” 4.(2022·贵州毕节中考)下图是常用的一些工具,它给我们带来了很多便利。其中属于费力杠杆 的是( ) 5.如图所示,杠杆 AOB 能绕 O 点转动。在 A 点挂一重物 G,为使杠杆保持平衡且用力最小,在
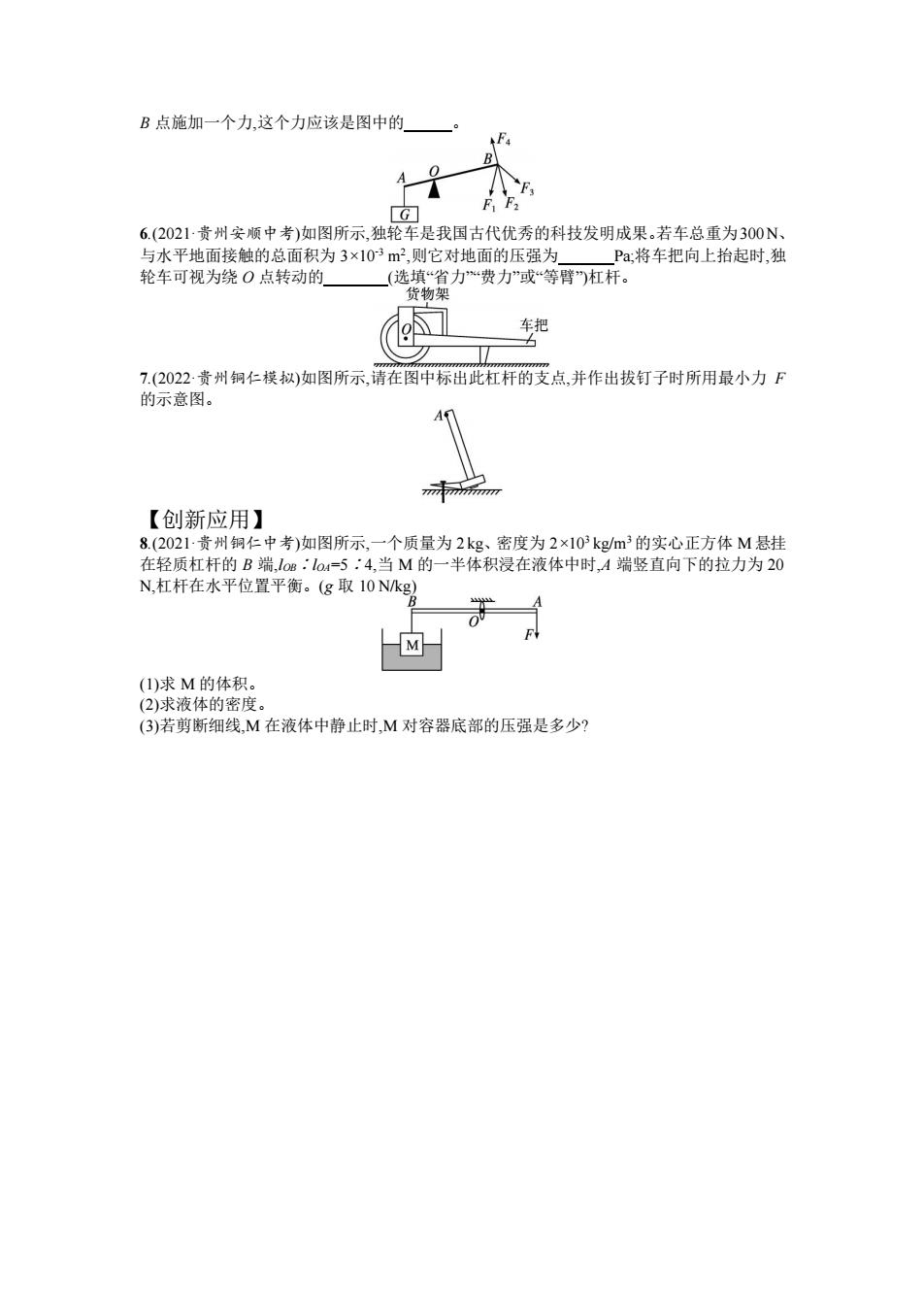
B点施加一个力,这个力应该是图中的 G 6.(2021·贵州安顺中考)如图所示,独轮车是我国古代优秀的科技发明成果。若车总重为300N、 与水平地面接触的总面积为3×103m2,则它对地面的压强为Pa将车把向上抬起时,独 轮车可视为绕O点转动的 (选填“省力“费力”或“等臂杠杆。 货物架 车把 7.(2022贵州铜仁模拟)如图所示,请在图中标出此杠杆的支点,并作出拔钉子时所用最小力F 的示意图。 【创新应用】 8.(2021·贵州铜仁中考)如图所示,一个质量为2kg、密度为2×103kgm3的实心正方体M悬挂 在轻质杠杆的B端,1os:lO4=5,4,当M的一半体积浸在液体中时,A端竖直向下的拉力为20 N,杠杆在水平位置平衡。(g取10Nkg) (1)求M的体积。 (2)求液体的密度: (3)若剪断细线,M在液体中静止时,M对容器底部的压强是多少?
B 点施加一个力,这个力应该是图中的 。 6.(2021·贵州安顺中考)如图所示,独轮车是我国古代优秀的科技发明成果。若车总重为300 N、 与水平地面接触的总面积为 3×10-3 m2 ,则它对地面的压强为 Pa;将车把向上抬起时,独 轮车可视为绕 O 点转动的 (选填“省力”“费力”或“等臂”)杠杆。 7.(2022·贵州铜仁模拟)如图所示,请在图中标出此杠杆的支点,并作出拔钉子时所用最小力 F 的示意图。 【创新应用】 8.(2021·贵州铜仁中考)如图所示,一个质量为 2 kg、密度为 2×103 kg/m3 的实心正方体 M 悬挂 在轻质杠杆的 B 端,lOB∶lOA=5∶4,当 M 的一半体积浸在液体中时,A 端竖直向下的拉力为 20 N,杠杆在水平位置平衡。(g 取 10 N/kg) (1)求 M 的体积。 (2)求液体的密度。 (3)若剪断细线,M 在液体中静止时,M 对容器底部的压强是多少?

【素能演练提升】 1.C2.B3.C4.B 5.F26.1×105省力 7.如图所示 7777772 8.(1)1×103m3(2)0.8×103kg/m3(3)1200Pa 解析(由p严可得正方体M的体积 M严= 2kg PM2x103 kg/m3 =1×103m3。 (2)物体M的重力 G=mg=2kg×10N/kg=20N 当M的一半体积浸在液体中时,由杠杆平衡条件可得 (G-F)×loB=Fxla4 解得F=4N F*印淡g/4=D8N 解得液体的密度 p液=0.8×103kgm3。 (3)若剪断细线,由于M的密度大于液体的密度,M将下沉、沉底,此时M受到液体的浮力 F*'=p凌g'e'=p液g'M=0.8×103kg/m3×10N/g×1×103m3-8N M对容器底部的压力 Fs=G-F浮=20N-8N=12N 正方体M的体积M=P=1×103m M的边长1=0.1m 受力面积S=P=(0.1m)2=1×102m2 M对容器底部的压强 =1200Pa
【素能·演练提升】 1.C 2.B 3.C 4.B 5.F2 6.1×105 省力 7.如图所示 8.(1)1×10-3 m3 (2)0.8×103 kg/m3 (3)1 200 Pa 解析 (1)由 ρ= 𝑚 𝑉可得正方体 M 的体积 VM= 𝑚 𝜌M = 2kg 2×10 3 kg/m3 =1×10-3 m3。 (2)物体 M 的重力 G=mg=2 kg×10 N/kg=20 N 当 M 的一半体积浸在液体中时,由杠杆平衡条件可得 (G-F 浮)×lOB=F×lOA 解得 F 浮=4 N F 浮=ρ 液 gV 排=ρ 液 g· 1 2 VM 解得液体的密度 ρ 液=0.8×103 kg/m3。 (3)若剪断细线,由于 M 的密度大于液体的密度,M 将下沉、沉底,此时 M 受到液体的浮力 F 浮'=ρ 液 gV 排'=ρ 液 gVM=0.8×103 kg/m3×10 N/kg×1×10-3 m3=8 N M 对容器底部的压力 F 压=G-F 浮=20 N-8 N=12 N 正方体 M 的体积 VM=l3=1×10-3 m3 M 的边长 l=0.1 m 受力面积 S=l2=(0.1 m)2=1×10-2 m2 M 对容器底部的压强 p= 𝐹压 𝑆 = 12N 1×10 -2 m2 =1 200 Pa