
统计学习理论及应用 第十讲非监督学习 编写:文泉、陈娟 电子科技大学 计算机科学与工程学院
统计学习理论及应用 第十讲 非监督学习 编写:文泉、陈娟 电子科技大学 计算机科学与工程学院

主目录 ①K-Means聚类算法(Clustering Algorithm) 2 网页排序PageRank 1/32
主目录 1 K-Means 聚类算法 (Clustering Algorithm) 2 网页排序 PageRank 1 / 32

一级目录 ①K-Means聚类算法(Clustering Algorithm) ②网页排序PageRank 2/32
一级目录 1 K-Means 聚类算法 (Clustering Algorithm) 2 网页排序 PageRank 2 / 32

l.K-Means聚类算法(Clustering Algorithm) In the clustering problem,we are given a training set {x(),...x(,x()ER", and want to group the data into a few cohesive"clusters."No labels(are given. The k-means clustering algorithm is as follows: Initialize cluster centroidsE R",j=1,2,...,k,randomly. 2 Repeat until convergence: For each training samplex(,set c0=argmin|lr0-马l2 2 For every cluster centroid i,set ∑l(c0=r0 ∑1I(c0=) } I()is the indicator function. 3/32
1. K-Means 聚类算法 (Clustering Algorithm) ▶ In the clustering problem, we are given a training set {x (1) , . . . , x (m)}, x (i) ∈ R n , and want to group the data into a few cohesive “clusters.” No labels y (i) are given. ▶ The k-means clustering algorithm is as follows: 1 Initialize cluster centroids µj ∈ R n , j = 1, 2, . . . , k, randomly. 2 Repeat until convergence: { 1 For each training sample x (i) , set c (i) = arg min j ∥x (i) − µj∥2 2 For every cluster centroid µj , set µj = Pm i=1 I(c (i) = j)x (i) Pm i=1 I(c (i) = j) } • I(·) is the indicator function. 3 / 32

一、二级目录 ① K-Means聚类算法(Clustering Algorithm) 。解释Explanation o收敛性Convergence of K-Means o矩阵建模Matrix Modelling of K-Means 4/32
一、二级目录 1 K-Means 聚类算法 (Clustering Algorithm) 解释 Explanation 收敛性 Convergence of K-Means 矩阵建模 Matrix Modelling of K-Means 4 / 32

l.1.解释Explanation k(hyper-parameter of the algorithm)is the number of clusters we want to find Cluster centroids urepresent our current guesses for the positions of the centers of the clusters. To initialize the cluster centroids we could choose k training sample randomly, and set the cluster centroids to be equal to the values of these k examples. The inner-loop of the algorithm repeatedly carries out two steps: .Assigning each training samplex(to the closest cluster centroid. Moving each cluster centroid to the mean of the samples assigned to it. 5/32
1.1. 解释 Explanation ▶ k (hyper-parameter of the algorithm) is the number of clusters we want to find ▶ Cluster centroids µj represent our current guesses for the positions of the centers of the clusters. To initialize the cluster centroids we could choose k training sample randomly, and set the cluster centroids to be equal to the values of these k examples. ▶ The inner-loop of the algorithm repeatedly carries out two steps: • Assigning each training sample x (i) to the closest cluster centroid µj . • Moving each cluster centroid µj to the mean of the samples assigned to it. 5 / 32
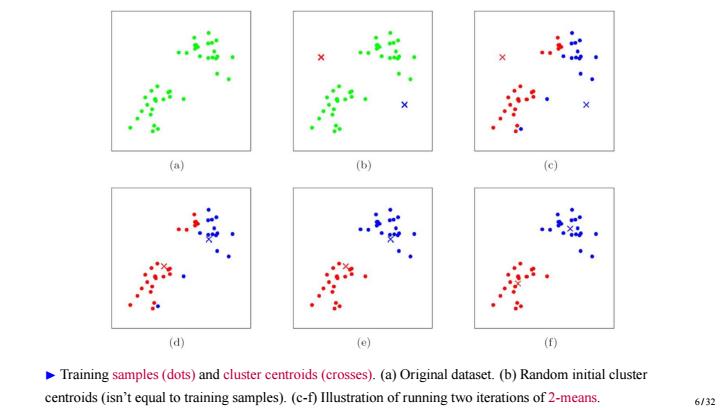
(a) (b) (c) (d) (e) () Training samples (dots)and cluster centroids(crosses).(a)Original dataset.(b)Random initial cluster centroids (isn't equal to training samples).(c-f)Illustration of running two iterations of 2-means. 6/32
▶ Training samples (dots) and cluster centroids (crosses). (a) Original dataset. (b) Random initial cluster centroids (isn’t equal to training samples). (c-f) Illustration of running two iterations of 2-means. 6 / 32

一、二级目录 K-Means聚类算法(Clustering Algorithm) o解释Explanation o收敛性Convergence of K-Means o矩阵建模Matrix Modelling of K-Means 7/32
一、二级目录 1 K-Means 聚类算法 (Clustering Algorithm) 解释 Explanation 收敛性 Convergence of K-Means 矩阵建模 Matrix Modelling of K-Means 7 / 32

l.2.收敛性Convergence of K-Means Define the distortion function to be: m Jlc,)=∑lr0-4enl2 i=1 Jmeasures the sum of squared distances between each training samplex(and the cluster centroid u(o to which it has been assigned. k-means is exactly coordinate descent onJ. holding u fixed,minimizes Jw.r.t.c. 2 holding c fixed,minimizesJw.r.t.u. Jmust monotonically decrease,and the value ofJ must converge.Usually,this implies that c and u will converge too. 8/32
1.2. 收敛性 Convergence of K-Means ▶ Define the distortion function to be: J(c, µ) = Xm i=1 ∥x (i) − µc (i)∥2 ▶ J measures the sum of squared distances between each training sample x (i) and the cluster centroid µc (i) to which it has been assigned. ▶ k-means is exactly coordinate descent on J. 1 holding µ fixed, minimizes J w.r.t. c. 2 holding c fixed, minimizes J w.r.t. µ. ▶ J must monotonically decrease, and the value of J must converge. Usually, this implies that c and µ will converge too. 8 / 32

局部最小值Local Minima of K-Means Distortion functionJ is a non-convex function,and so coordinate descent onJ is not guaranteed to converge to the global minimum. k-means can be susceptible to local optima. To avoid getting stuck in bad local minima,one common thing to do is run k-means many times(using different random initial values for the cluster centroids ui).Then,pick the one that gives the lowest distortion J(c,u). 9/32
局部最小值 Local Minima of K-Means ▶ Distortion function J is a non-convex function, and so coordinate descent on J is not guaranteed to converge to the global minimum. ▶ k-means can be susceptible to local optima. ▶ To avoid getting stuck in bad local minima, one common thing to do is run k-means many times (using different random initial values for the cluster centroids µj). Then, pick the one that gives the lowest distortion J(c, µ). 9 / 32