
统计学习理论及应用 第六讲非线性分类模型多层感知机 编写:文泉、陈娟 电子科技大学 计机科学与工程学院
统计学习理论及应用 第六讲 非线性分类模型-多层感知机 编写:文泉、陈娟 电子科技大学 计算机科学与工程学院

目录 4 多层感知机到底在做什么? 历史进程 Tilling(耕种,耕作)算法 预备知识 6 可微激活函数函的多层感知机学习方法 ⊙采用线性激活函数的神经元 o误差e的表示 。采用阈值激活函数的神经元 ·误差的反向传播 。采用S形激活函数的神经元 。反向传播算法 3 异或问题 Q计算例子 1/66
目录 1 历史进程 2 预备知识 采用线性激活函数的神经元 采用阈值激活函数的神经元 采用 S 形激活函数的神经元 3 异或问题 4 多层感知机到底在做什么? 5 Tilling(耕种,耕作)算法 6 可微激活函数函的多层感知机学习方法 误差 e 的表示 误差的反向传播 反向传播算法 计算例子 1 / 66

7.1.历史进程 第一代神经网络 感知机(~1960) Bomb Toy 输出单元: 类标签 利用人工设计的特征 层,学习各个特征权重 w用以识别模式。 非自适应的 。有干净、漂亮的学 人工设计特 习算法来调节权重 征 W o ·感知机局限于能学 习的任务范围。 输入数据: 图像像素值 2/66
7.1. 历史进程 第一代神经网络 感知机(∼1960) 利用人工设计的特征 层,学习各个特征权重 w 用以识别模式。 有干净、漂亮的学 习算法来调节权重 w 。 感知机局限于能学 习的任务范围。 Bomb Toy 输出单元: 类标签 非自适应的 人工设计特 征 输入数据: 图像像素值 2 / 66
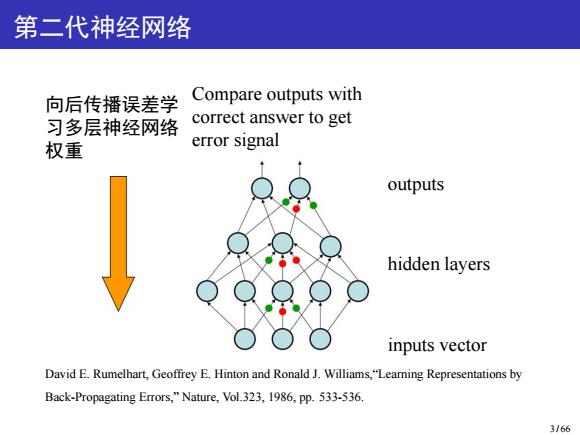
第二代神经网络 向后传播误差学 Compare outputs with 习多层神经网络 correct answer to get 权重 error signal outputs hidden layers inputs vector David E.Rumelhart,Geoffrey E.Hinton and Ronald J.Williams,"Learning Representations by Back-Propagating Errors,"Nature,Vol.323,1986,pp.533-536. 3/66
第二代神经网络 向后传播误差学 习多层神经网络 权重 Compare outputs with correct answer to get error signal outputs hidden layers inputs vector David E. Rumelhart, Geoffrey E. Hinton and Ronald J. Williams,“Learning Representations by Back-Propagating Errors,” Nature, Vol.323, 1986, pp. 533-536. 3 / 66
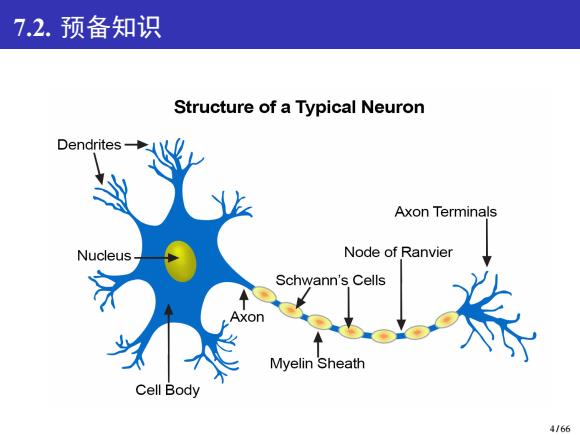
7.2.预备知识 Structure of a Typical Neuron Dendrites- Axon Terminals Nucleus Node of Ranvier Schwann's Cells Axon Myelin Sheath Cell Body 4/66
7.2. 预备知识 4 / 66
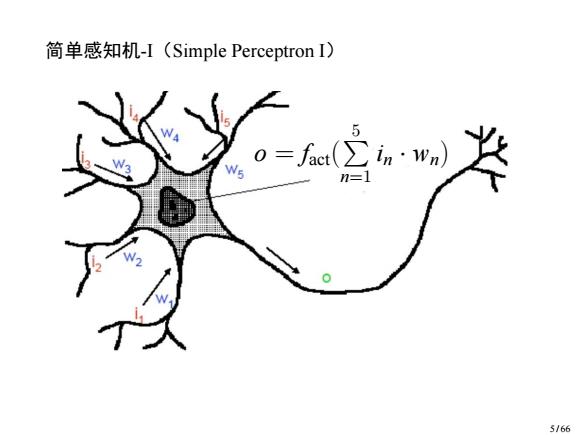
简单感知机-I(Simple Perceptron I) 5 5/66
简单感知机-I(Simple Perceptron I) o = fact( P 5 n=1 in · wn) 5 / 66
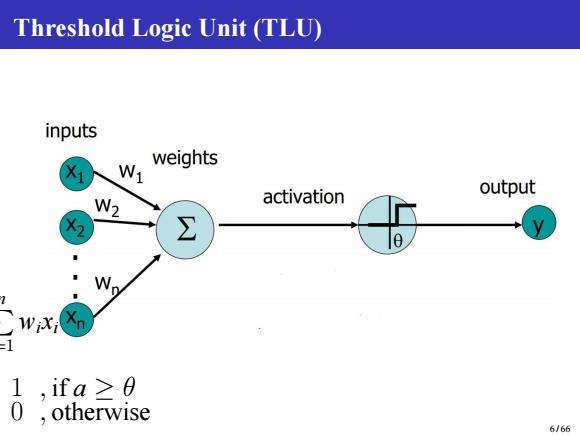
Threshold Logic Unit (TLU) inputs W1 weights output W2 activation =1 1,ifa≥0 0,otherwise 6/66
Threshold Logic Unit (TLU) a = P n i=1 wixi y = n 1 , if a ≥ θ 0 , otherwise 6 / 66

Activation Functions(激活函数) threshold linear 二 x)=中 piece-wise linear sigmoid f=f(x)(1-f(x) E:0 S形(Sigmoid)函数:连 续,光滑,严格单调, 关于(0,0.5)中心对称的 阈值函数。 7/66
Activation Functions(激活函数) fs(x) = 1 1+e−x f ′ s = f (x)(1 − f (x)) S 形 (Sigmoid) 函数:连 续,光滑,严格单调, 关于 (0,0.5) 中心对称的 阈值函数。 7 / 66
Sigmoidal Functions(S形函数) v) Logistic function: 1 p(y)= 1+e-y where -10-864-2246810 i=1 ·y是神经元j的感应场(induced field). ·Sigmoidal functions是激活函数通用的形式 。a→0∞→P→阈值函数 。Sigmoidal functions可求导 8/66
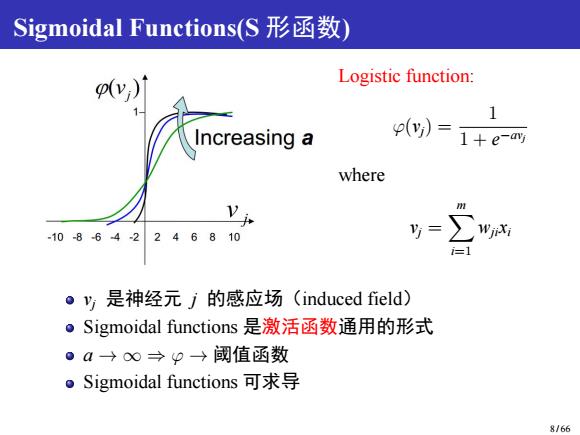
Sigmoidal Functions(S 形函数) Logistic function: φ(vj) = 1 1 + e −avj where vj = Xm i=1 wjixi vj 是神经元 j 的感应场(induced field) Sigmoidal functions 是激活函数通用的形式 a → ∞ ⇒ φ → 阈值函数 Sigmoidal functions 可求导 8 / 66

7.2.1.采用线性激活函数的神经元 inputs weights X1 N output W2 activation ∑ a n y=p(a=a=∑ WiXi 9166
7.2.1. 采用线性激活函数的神经元 a = P n i=1 wixi y = φ(a) = a = P n i=1 wixi 9 / 66