
统计学习理论及应用 第五讲 支持向量机 编写:文泉、陈娟 电子科技大学 计机科学与工程学院
统计学习理论及应用 第五讲 支持向量机 编写:文泉、陈娟 电子科技大学 计算机科学与工程学院

目录 OKKT条件 O核函数的定义 感知机存在的一个问题 O线性可分SVM学习的 。核函数的选取 线性可分SVM 对偶算法 O核技巧在SVM中的应 OSVM的种类 线性不可分SVM 用 。函数间隔和几何间隔 O线性SVM学习的对偶 O非线性SVM算法 。学习的原始最优化问 算法 题 5 序列最小最优化算法 O线性SVM学习算法 。凸优化问题 OSMO算法的基本思路 O线性不可分时的SV O线性可分SVM学习算 ⊙两变量二次规划的求 Q合页损失函数 法一最大间隔法 解方法 。支持向量与间隔边界 非线性SVM与核函数 。两个变量的选择方法 ○拉格朗日对偶性 。希尔伯特空间 OSMO算法 1/154
目录 1 感知机存在的一个问题 2 线性可分 SVM SVM 的种类 函数间隔和几何间隔 学习的原始最优化问 题 凸优化问题 线性可分 SVM 学习算 法—最大间隔法 支持向量与间隔边界 拉格朗日对偶性 KKT 条件 线性可分 SVM 学习的 对偶算法 3 线性不可分 SVM 线性 SVM 学习的对偶 算法 线性 SVM 学习算法 线性不可分时的 SV 合页损失函数 4 非线性 SVM 与核函数 希尔伯特空间 核函数的定义 核函数的选取 核技巧在 SVM 中的应 用 非线性 SVM 算法 5 序列最小最优化算法 SMO 算法的基本思路 两变量二次规划的求 解方法 两个变量的选择方法 SMO 算法 1 / 154

知识点: 。支持向量机核心思想 ·凸优化的基本思想和概念 。支持向量机的公式推导 重点与难点: 。重点:支持向量机核心思想,凸优化的基本思想和概 念,支持向量机的公式推导。 。难点:KKT(Karush-Kuhn-Tucker)条件的理解和推导。 2/154
知识点: 支持向量机核心思想 凸优化的基本思想和概念 支持向量机的公式推导 重点与难点: 重点:支持向量机核心思想,凸优化的基本思想和概 念,支持向量机的公式推导。 难点:KKT(Karush-Kuhn-Tucker)条件的理解和推导。 2 / 154

5.1.感知机存在的一个问题 Linear Classifiers X g yest ·denotes+1 。denotes-1 How would you classify this data? 3/154
5.1. 感知机存在的一个问题 Linear Classifiers 3 / 154
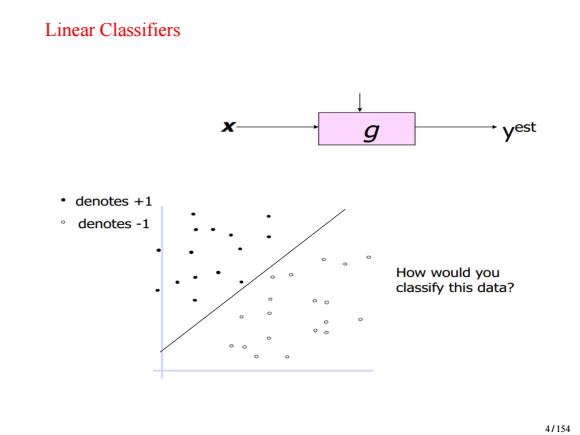
Linear Classifiers g yest ·denotes+1 。 denotes-1 How would you classify this data? 4/154
Linear Classifiers 4 / 154

Linear Classifiers g yest ·denotes+1 。 denotes-1 How would you classify this data? 5/154
Linear Classifiers 5 / 154
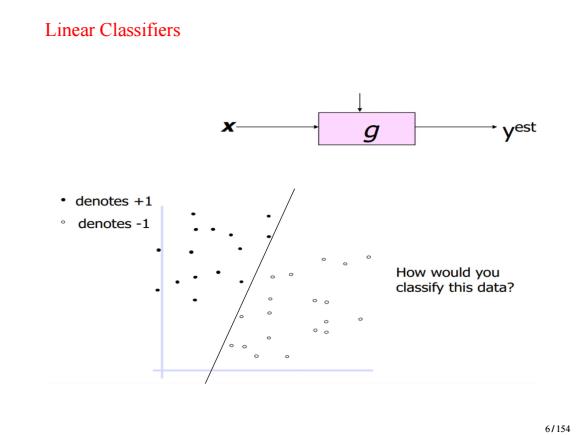
Linear Classifiers X g yest ·denotes+1 。 denotes-1 How would you classify this data? 6/154
Linear Classifiers 6 / 154
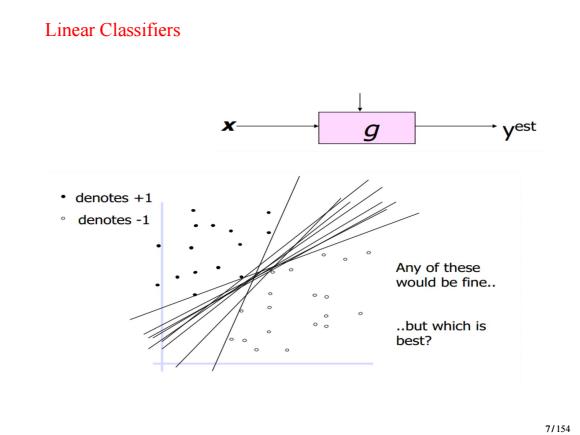
Linear Classifiers g yest ·denotes+1 。denotes-1 Any of these would be fine.. ..but which is best? 7/154
Linear Classifiers 7 / 154

5.2.线性可分SVM 5.2.1.SVM的种类 ·数据集的线性可分性:给定一个数据集 T={(x1,h),(x2,2,,(xw,w)}, 其中x∈X=R”,y∈y={+1,-1},i=1,2,.,N,如 果存在某个超平面S w·x+b=0 能够将数据集的正实例点和负实例点完全正确地划分到超 平面的两侧,即 ·对所有片=+1的实例i有w·x+b>0, 。对所有片=-1的实例i有w·x+b<0, 则称数据集T为线性可分数据集(linearly separable dataset);否则,称T为线性不可分数据集。 8/154
5.2. 线性可分 SVM 5.2.1. SVM 的种类 ▶ 数据集的线性可分性:给定一个数据集 T = {(x1, y1),(x2, y2), . . . ,(xN, yN)}, 其中 xi ∈ X = R n , yi ∈ Y = {+1, −1}, i = 1, 2, . . . , N,如 果存在某个超平面 S w · x + b = 0 能够将数据集的正实例点和负实例点完全正确地划分到超 平面的两侧,即 对所有 yi = +1 的实例 i 有 w · xi + b > 0, 对所有 yi = −1 的实例 i 有 w · xi + b < 0, 则称数据集 T 为线性可分数据集(linearly separable dataset);否则,称 T 为线性不可分数据集。 8 / 154

线性分类器 ·学习的目标是在特征空间中找到一个分离超平面,能将 实例分到不同的类。分离超平面对应于方程 w·x+b=0 ·法向量W和截距b决定,分离超平面将特征空间划分 为两部分。法向量指向的一侧为正类,另一侧为负类。 ·例如,分离超平面对应于方程w·x+b=0,它由法向量 w和截距b决定。考虑同一分离平面不同的法向量: 1.w1=(1,1)T,b=0 2.w2=-w1=(-1,-1)T,b=0 w1和w2所表示的分离超平面的正、负类位置正好相反。 9/154
线性分类器 ▶ 学习的目标是在特征空间中找到一个分离超平面,能将 实例分到不同的类。分离超平面对应于方程 w · x + b = 0, ▶ 法向量 w 和截距 b 决定,分离超平面将特征空间划分 为两部分。法向量指向的一侧为正类,另一侧为负类。 ▶ 例如,分离超平面对应于方程 w · x + b = 0,它由法向量 w 和截距 b 决定。考虑同一分离平面不同的法向量: 1. w1 = (1, 1)T , b = 0 2. w2 = −w1 = (−1, −1)T , b = 0 w1 和 w2 所表示的分离超平面的正、负类位置正好相反。 9 / 154