
Statistical Learning Theory and Applications Lecture 6 Multilayer Perceptron Instructor:Quan Wen SCSE@UESTC Fal,2021
Statistical Learning Theory and Applications Lecture 6 Multilayer Perceptron Instructor: Quan Wen SCSE@UESTC Fall, 2021

Outline (Level 1) ①History 2Preparatory knowledge ③XOR problem 4 MLP is doing what? ⑤Tilling Algorithm 6 Learning algorithm for MLP of differentiable activation function 1/77
Outline (Level 1) 1 History 2 Preparatory knowledge 3 XOR problem 4 MLP is doing what? 5 Tilling Algorithm 6 Learning algorithm for MLP of differentiable activation function 1 / 77

Outline (Level 1) ●History Preparatory knowledge XOR problem MLP is doing what? Tilling Algorithm Learning algorithm for MLP of differentiable activation function 2/77
Outline (Level 1) 1 History 2 Preparatory knowledge 3 XOR problem 4 MLP is doing what? 5 Tilling Algorithm 6 Learning algorithm for MLP of differentiable activation function 2 / 77
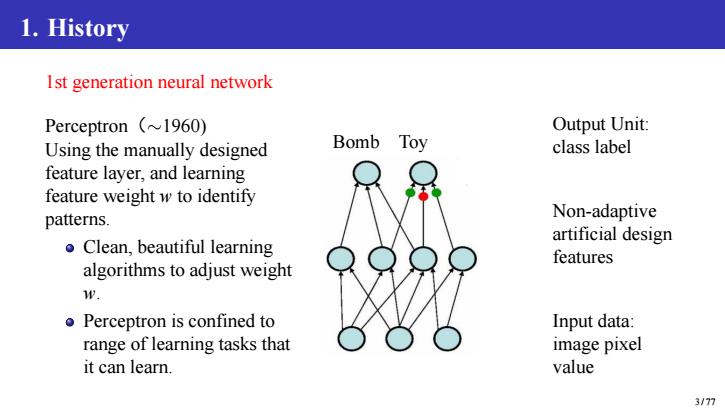
1.History Ist generation neural network Perceptron (~1960) Output Unit: Using the manually designed Bomb Toy class label feature layer,and learning feature weight w to identify patterns. Non-adaptive Clean,beautiful learning artificial design features algorithms to adjust weight W. o Perceptron is confined to Input data: range of learning tasks that image pixel it can learn. value 3/77
1. History 1st generation neural network Perceptron(∼1960) Using the manually designed feature layer, and learning feature weight w to identify patterns. Clean, beautiful learning algorithms to adjust weight w. Perceptron is confined to range of learning tasks that it can learn. Bomb Toy Output Unit: class label Non-adaptive artificial design features Input data: image pixel value 3 / 77

2nd generation neural network Backward propagation error to learn weights of Compare outputs with correct multilayer neural answer to get error signal networks outputs hidden layers inputs vector Rumelhart,D.E.,Hinton,G.E.,and Williams,backpropagating errors.Nature,323,533-536. 4/77
2nd generation neural network Backward propagation error to learn weights of multilayer neural networks Compare outputs with correct answer to get error signal outputs hidden layers inputs vector Rumelhart, D. E., Hinton, G. E., and Williams,backpropagating errors. Nature, 323, 533-536. 4 / 77

Outline (Level 1) History Preparatory knowledge XOR problem MLP is doing what? Tilling Algorithm Learning algorithm for MLP of differentiable activation function 5/77
Outline (Level 1) 1 History 2 Preparatory knowledge 3 XOR problem 4 MLP is doing what? 5 Tilling Algorithm 6 Learning algorithm for MLP of differentiable activation function 5 / 77
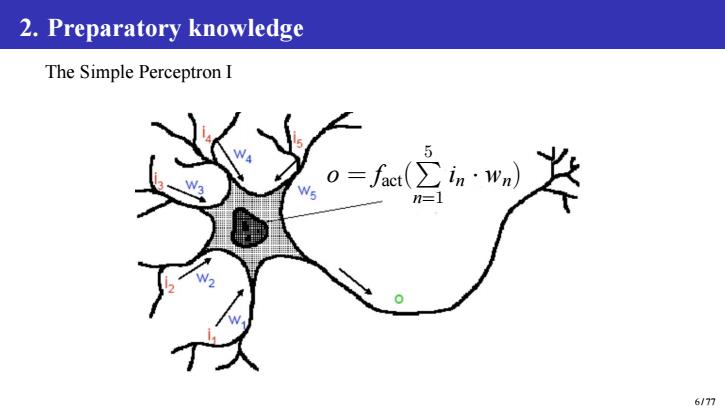
2.Preparatory knowledge The Simple Perceptron I 5 n=1 6/77
2. Preparatory knowledge The Simple Perceptron I o = fact( P 5 n=1 in · wn) 6 / 77
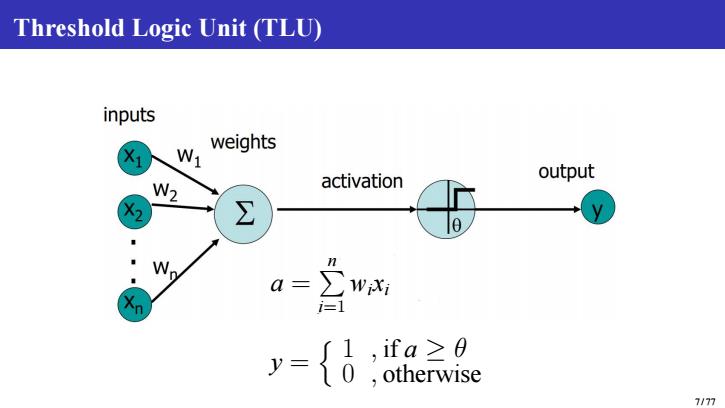
Threshold Logic Unit (TLU) inputs X1 N weights activation output W2 X ∑ o n a= WiXi y= {0 ,ifa≥0 otherwise 7/77
Threshold Logic Unit (TLU) a = P n i=1 wixi y = n 1 , if a ≥ θ 0 , otherwise 7 / 77
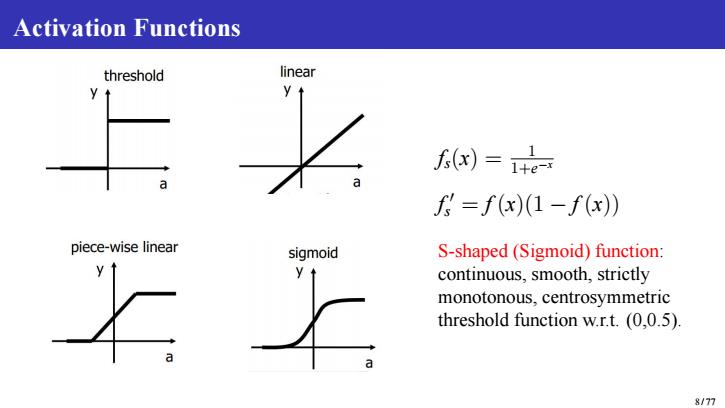
Activation Functions threshold linear )=+ =f(x)(1-f(x)) piece-wise linear sigmoid S-shaped(Sigmoid)function: continuous,smooth,strictly monotonous,centrosymmetric threshold function w.r.t.(0,0.5). 8/77
Activation Functions fs(x) = 1 1+e−x f ′ s = f (x)(1 − f (x)) S-shaped (Sigmoid) function: continuous, smooth, strictly monotonous, centrosymmetric threshold function w.r.t. (0,0.5). 8 / 77

Sigmoidal Functions Logistic function: Increasing a p(y)=1+e-y where 108642246810 ∑ WjiXi i=1 v is the induced field of neuron j oSigmoidal functions is the general form of activation function ●a→o→p→threshold function Sigmoidal functions is differentiable 9177
Sigmoidal Functions Logistic function: φ(vj) = 1 1 + e −avj where vj = Xm i=1 wjixi vj is the induced field of neuron j Sigmoidal functions is the general form of activation function a → ∞ ⇒ φ → threshold function Sigmoidal functions is differentiable 9 / 77