
第二章 一、平均偏差 定量分析中的误 二、标准偏差 差与数据处理 三、平均值的标准偏差 四、置信度与置信区间 第二节 分析结果的数据 处理 下页 螺助】 越回
第二章 定量分析中的误 差与数据处理 一、平均偏差 二、标准偏差 三、平均值的标准偏差 四、置信度与置信区间 第二节 分析结果的数据 处理

平均偏差 平均偏差又称算术平均偏差, 用来表示一组数据的精密度。 平均偏差: a=∑x-x 特点:简单; 缺点:大偏差得不到应有反映。 2024/9/13 上页 下页 返回
2024/9/13 一、 平均偏差 平均偏差又称算术平均偏差, 用来表示一组数据的精密度。 平均偏差: 特点:简单; 缺点:大偏差得不到应有反映。 n X X d − =

二、 标准偏差 标准偏差又称均方根偏差; 标准偏差的计算分两种情况: 1. 当测定次数趋于无穷大时 标准偏差: o=V∑X-}/n μ为无限多次测定的平均值(总体平均值);即: limX= 1-→do 当消除系统误差时,即为真值。 2.有限测定次数 标准偏差:s=V∑K-ヅa-) 相对标准偏差:(变异系数)C%=S/X 2024/9/13 上页 下页 返回
2024/9/13 二、 标准偏差 相对标准偏差 :(变异系数)CV% = S / X 标准偏差又称均方根偏差; 标准偏差的计算分两种情况: 1.当测定次数趋于无穷大时 标准偏差 : μ 为无限多次测定 的平均值(总体平均值); 即: 当消除系统误差时,μ即为真值。 2.有限测定次数 标准偏差 : = (X − ) / n 2 = ( − ) /( −1) 2 s X X n = → X n lim
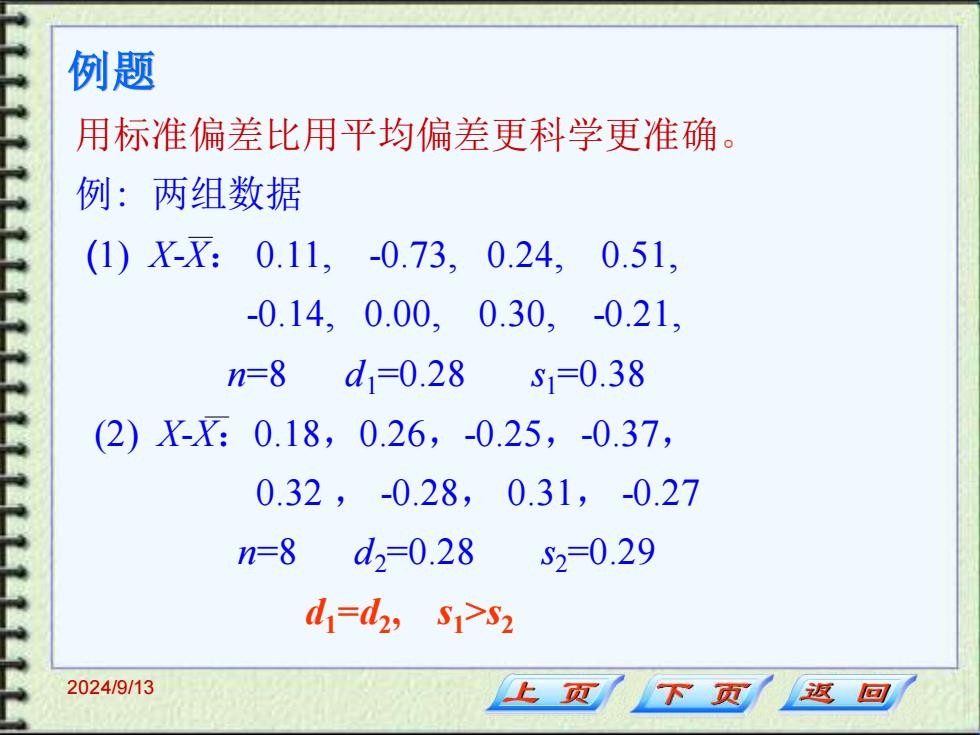
例题 用标准偏差比用平均偏差更科学更准确。 例:两组数据 (1)X-X: 0.11,-0.73,0.24,0.51, 0.14,0.00,0.30,-0.21, n=8d1=0.28s1=0.38 (2)X-X:0.18,0.26,-0.25,-0.37, 0.32,-0.28,0.31,-0.27 n=8 d2=0.28 52=0.29 d=d,s-S2 2024/9/13 上页 下页 返回
2024/9/13 例题 用标准偏差比用平均偏差更科学更准确。 例: 两组数据 (1) X-X: 0.11, -0.73, 0.24, 0.51, -0.14, 0.00, 0.30, -0.21, n=8 d1=0.28 s1=0.38 (2) X-X:0.18,0.26,-0.25,-0.37, 0.32 , -0.28, 0.31, -0.27 n=8 d2=0.28 s2=0.29 d1=d2 , s1>s2
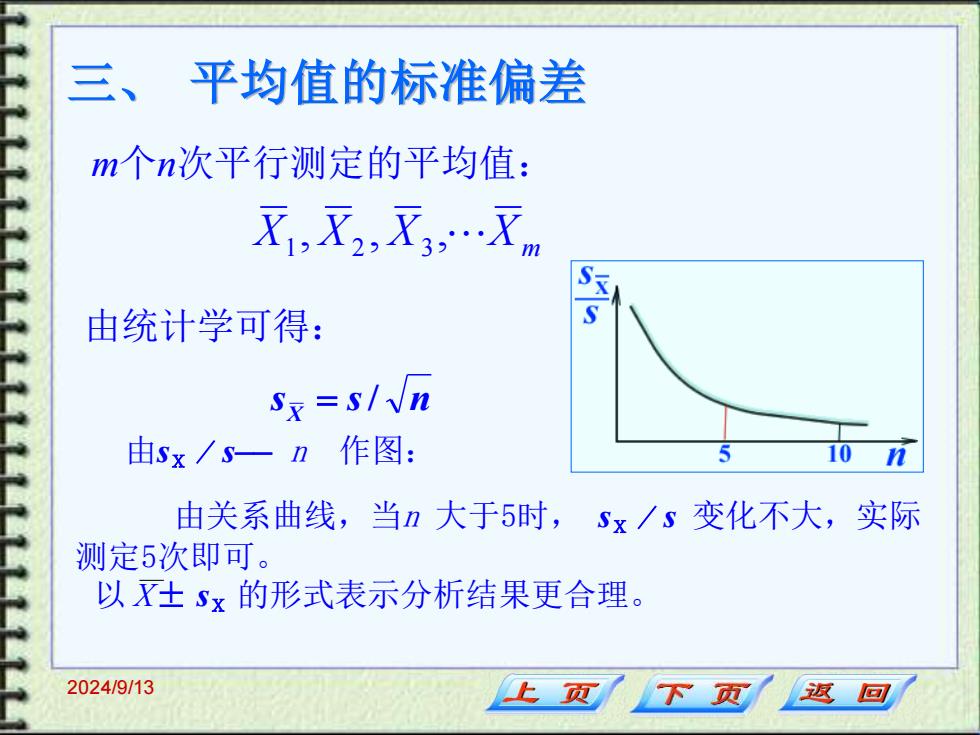
三、平均值的标准偏差 m个n次平行测定的平均值: 灭,X2,X3,.Xm 由统计学可得: Sx=s/n 由sx/s—n作图: 由关系曲线,当n大于5时,Sx/s变化不大,实际 测定5次即可。 以X士Sx的形式表示分析结果更合理。 2024/9/13 下页 返回
2024/9/13 三、 平均值的标准偏差 m个n次平行测定的平均值: 由关系曲线,当n 大于5时, sX/ s 变化不大,实际 测定5次即可。 以 X± sX 的形式表示分析结果更合理。 X X X X m , , , 1 2 3 s s n X = / 由统计学可得: 由sX/ s—— n 作图:
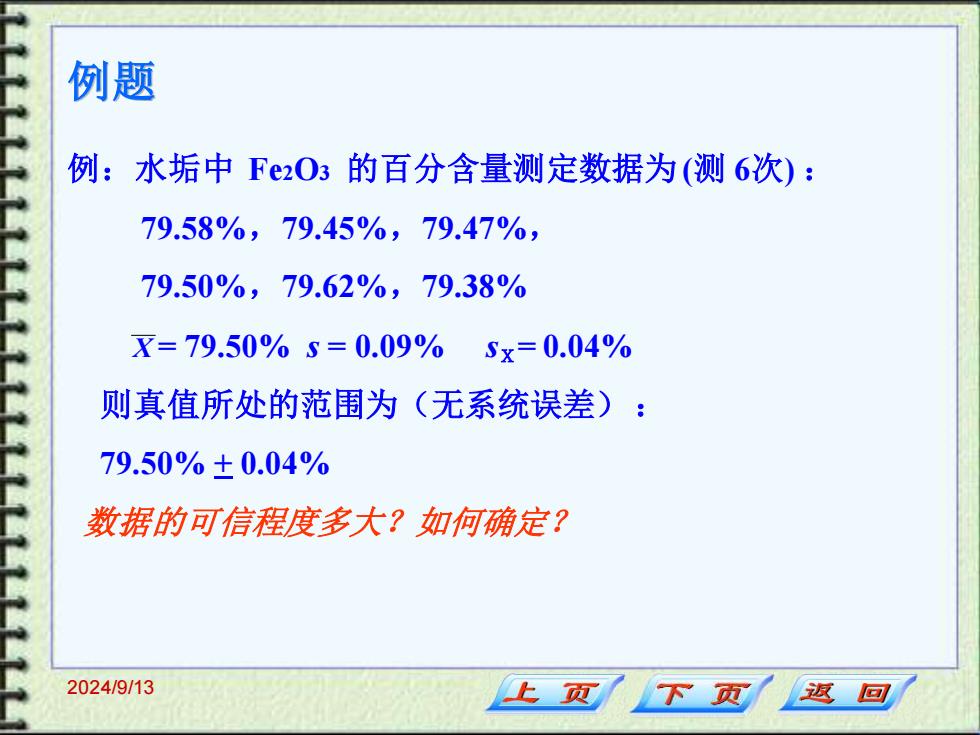
例题 例:水垢中F2O3的百分含量测定数据为(测6次): 79.58%,79.45%,79.47%, 79.50%,79.62%,79.38% =79.50%s=0.09%5x=0.04% 则真值所处的范围为(无系统误差): 79.50%±0.04% 数据的可信程度多大?如何确定? 2024/9/13 上页 下页 返回
2024/9/13 例题 例:水垢中 Fe2O3 的百分含量测定数据为(测 6次) : 79.58%,79.45%,79.47%, 79.50%,79.62%,79.38% X = 79.50% s = 0.09% sX= 0.04% 则真值所处的范围为(无系统误差) : 79.50% + 0.04% 数据的可信程度多大?如何确定?
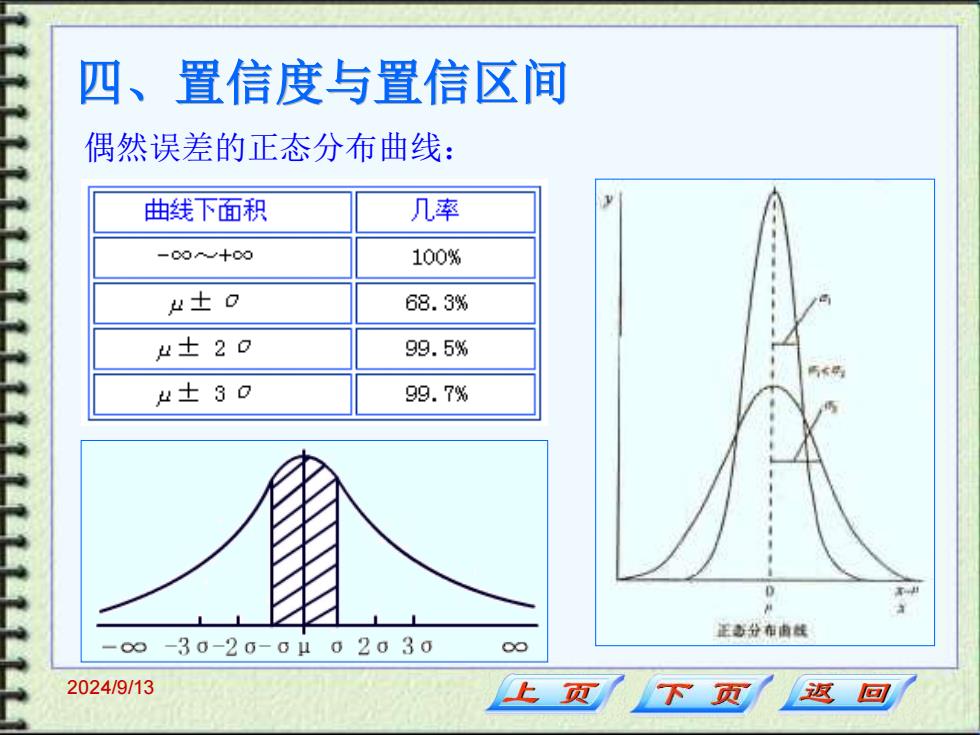
四、置信度与置信区间 偶然误差的正态分布曲线: 曲线下面积 几率 -00+00 100% 以士o 68.3% 以±2o 99.5% μ士30 99.7% D 正多分布南线 -∞-30-20-0μ02030 00 2024/9/13 上页 下页 返回
2024/9/13 四、置信度与置信区间 偶然误差的正态分布曲线:
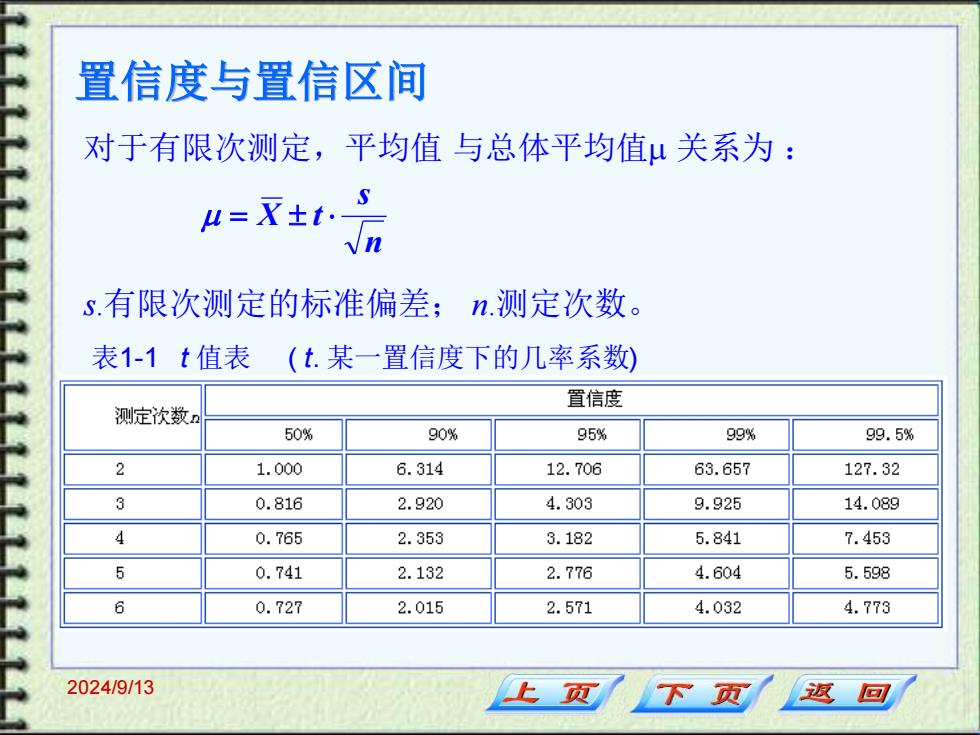
置信度与置信区间 对于有限次测定,平均值与总体平均值μ关系为: u=F±t.S s.有限次测定的标准偏差;n.测定次数。 表1-1t值表(t.某一置信度下的几率系数) 置信度 测定次数n 50% 90% 95% 99% 99.5% 2 1.000 6.314 12.706 63.657 127.32 3 0.816 2.920 4.303 9.925 14.089 4 0.765 2.353 3.182 5.841 7.453 5 0.741 2.132 2.776 4.604 5.598 6 0.727 2.015 2.571 4.032 4.773 2024/9/13 上页 下页 返回
2024/9/13 置信度与置信区间 s.有限次测定的标准偏差; n.测定次数。 对于有限次测定,平均值 与总体平均值 关系为 : n s = X t 表1-1 t 值表 ( t. 某一置信度下的几率系数)
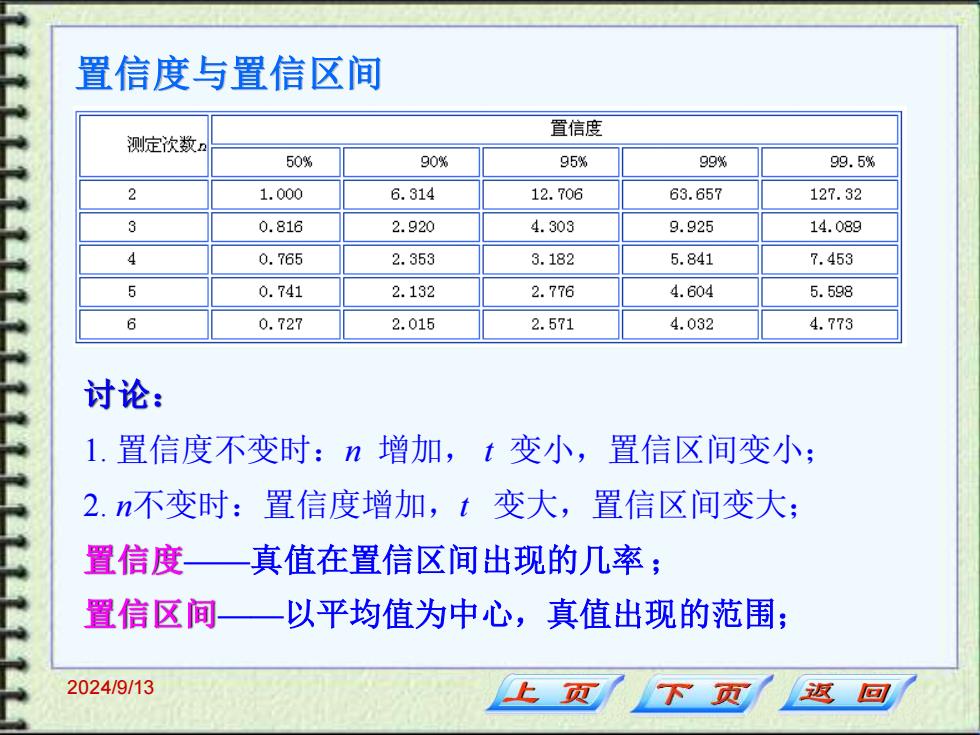
置信度与置信区间 置信度 测定次数n 50% 90% 95% 99% 99.5% 2 1.000 6.314 12.706 63.657 127.32 3 0.816 2.920 4.303 9.925 14.089 4 0.765 2.353 3.182 5.841 7.453 0.741 2.132 2.776 4.604 5.598 6 0.727 2.015 2.571 4.032 4.773 讨论: 1.置信度不变时:n增加,t变小,置信区间变小; 2.n不变时:置信度增加,t变大,置信区间变大; 置信度一真值在置信区间出现的几率; 置信区间一以平均值为中心,真值出现的范围; 2024/9/13 下页 返回
2024/9/13 置信度与置信区间 讨论: 1. 置信度不变时:n 增加, t 变小,置信区间变小; 2. n不变时:置信度增加,t 变大,置信区间变大; 置信度——真值在置信区间出现的几率; 置信区间——以平均值为中心,真值出现的范围;

内容选择: 第一节定量分析中的误差 第二节分析结果的数据处理 第三节定量分析数据的评价 第四节有效数字及其运算规则 第五节标准曲线的线性方程拟合 结枣《 2024/9/13 上页 返回
2024/9/13 内容选择: 第一节 定量分析中的误差 第二节 分析结果的数据处理 第三节 定量分析数据的评价 第四节 有效数字及其运算规则 第五节 标准曲线的线性方程拟合 结束