
第1章化学基础知识 1.1气体
第1章 化学基础知识 1.1 气体

1.1.1气体的状态方程 气体的最基本特征:具有可压缩性和扩散性。 人们将符合理想气体状态方程式的气体,称为 理想气体。 理想气体分子本身的体积相对于气体所占有体 积完全可以忽略,气体分子之间没有相互吸引和排 斥
气体的最基本特征:具有可压缩性和扩散性。 人们将符合理想气体状态方程式的气体,称为 理想气体。 理想气体分子本身的体积相对于气体所占有体 积完全可以忽略,气体分子之间没有相互吸引和排 斥。 1.1.1 气体的状态方程

1.理想气体状态方程式 pV=nRT R-摩尔气体常数 在STP(标准状况)下,p=101.325kPa,T=273.15K n=1.0mol时,Vm=22.414L=22.414×10-3m3 R=p'-101325Pa×22.414×103m3 nT 1.0mol×273.15K =8.314Pam3.mol-1.K- R=8.314KPa.L.mol-.K-
1. 理想气体状态方程式 pV = nRT R- 摩尔气体常数 在STP(标准状况)下,p =101.325kPa, T=273.15K n=1.0 mol时, Vm =22.414L=22.414×10-3m3 1 1 3 1 1 -3 3 8.314KPa L mol K 8.314Pa m mol K 1.0mol 273.15K 101325Pa 22.414 10 m − − − − = = = = R nT pV R

2.理想气体状态方程式的应用 (1).计算p,V,T,n四个物理量之一。 用于温度不太低,压力不太高的真实气体。 (2).气体摩尔质量的计算 pV=nRT m n= M pV= RT M M mRT M=Mg·mol-1 PL 4
m pV RT M = 4 (1). 计算p,V,T,n四个物理量之一。 (2). 气体摩尔质量的计算 2. 理想气体状态方程式的应用 用于温度不太低,压力不太高的真实气体。 1 M Mr g mol − = = = = = pV mRT M RT M m pV M m pV nRT n

3.气体密度的计算 mRT m M= pV M= p pM RT 5
m pV RT M = 5 3. 气体密度的计算 RT pM p RT M V m pV mRT M = = = =

例题 惰性气体氙能和氟形成多种氟化物XFx。实验 测定在80℃、15.6kPa时,某气态氟化氙试样的密度 为0.899(gdm3),试确定这种氟化氙的分子式。 解:求出摩尔质量,即可确定分子式。 设氟化氙的摩尔质量为M,密度为p(gdm3),质量为m(g), R应选用8.314(KPa'dm3mo1.K1)。 pY-RT=(R =骨=A% (0.899×8.314×353 15.6 2=169(gmol) 假设该氟化氙的分子式为XeFx,则有:131+19x=169, '.x=2,即该氟化氙的分子式为XeF2 6
6 惰性气体氙能和氟形成多种氟化物XeFx。实验 测定在80℃、15.6kPa时,某气态氟化氙试样的密度 为0.899(g·dm-3 ),试确定这种氟化氙的分子式。 解:求出摩尔质量,即可确定分子式。 设氟化氙的摩尔质量为M,密度为ρ(g·dm-3 ),质量为m(g), R应选用8.314(KPa·dm3·mol-1·K-1 )。 169(g mol ) 15.6 (0.899 8.314 353) ( )( ) ( ) ( ) −1 = = = = = = = p RT p RT V m pV mRT M RT M m pV nRT 假设该氟化氙的分子式为XeFx ,则有:131+19x = 169, ∴ x = 2,即该氟化氙的分子式为XeF2

1.1.2道尔顿分压定律 由两种或两种以上的不发生化学反应的气体混 合在一起组成的体系,称为混合气体。 组成混合气体的每种气体,都称为该混合气体 的组分气体。 例如,空气是混合气体,其中的O2,N2,C0, 等,均为空气这种混合气体的组分气体。 7
7 由两种或两种以上的不发生化学反应的气体混 合在一起组成的体系,称为混合气体。 组成混合气体的每种气体,都称为该混合气体 的组分气体。 例如,空气是混合气体,其中的O2,N2,CO2 等,均为空气这种混合气体的组分气体。 1.1.2 道尔顿分压定律

组分气体i的物质的量用n:表示,混合气 体的物质的量用n表示,则: n=∑n: i 组分气体i的摩尔分数用x:表示,则: i X= n 当组分气体单独存在且与混合气体具有相同 体积时,其所产生的压强称为该组分气体的分压, 记做p。关系如下: p:V总=n;RT
组分气体 i 的物质的量用 ni 表示,混合气 体的物质的量用 n 表示,则: 组分气体 i 的摩尔分数用 xi 表示,则: 当 组分气体单独存在且与混合气体具有相同 体积时,其所产生的压强称为该组分气体的分压, 记做 pi。关系如下: pi V总 = ni RT n = ni i xi = ni n

道尔顿分压定律 道尔顿(Dalton) 进行了大量实验,提 出了混合气体的分压定律 一混合气体的总 压等于各组分气体的分压之和。数学表达式 为: P总=∑P阳 9
9 道尔顿(Dalton)进行了大量实验,提 出了混合气体的分压定律 —— 混合气体的总 压等于各组分气体的分压之和。数学表达式 为: i i n RT p V = 道尔顿分压定律 p总 = pi i
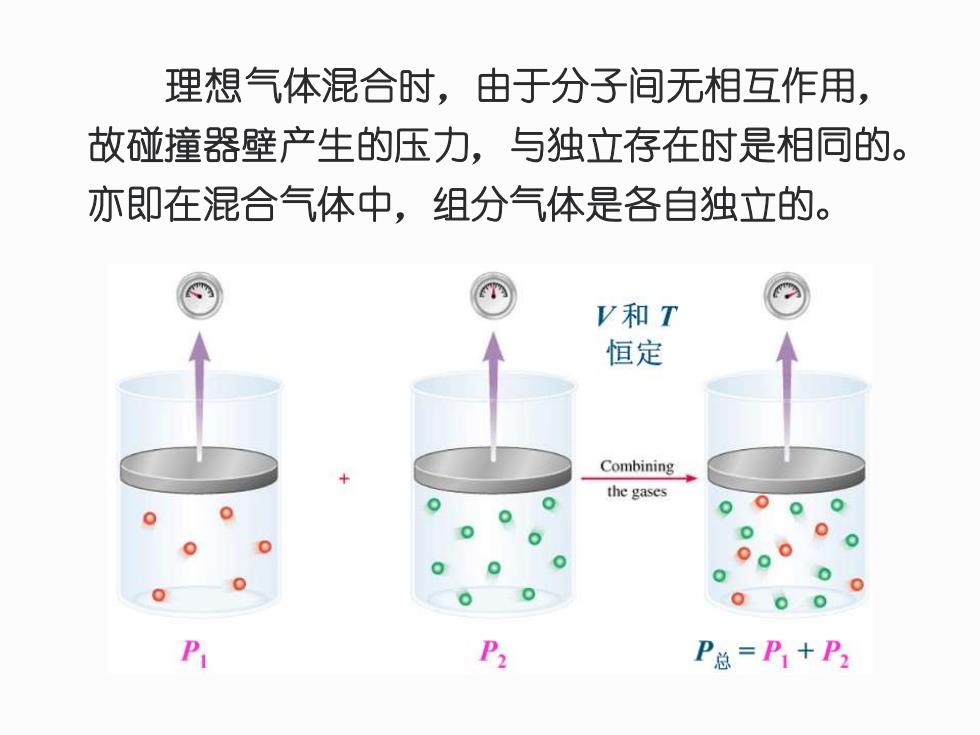
理想气体混合时,由于分子间无相互作用, 故碰撞器壁产生的压力,与独立存在时是相同的。 亦即在混合气体中,组分气体是各自独立的。 V和T 恒定 Combining the gases 0 0.0 000 P P2 P总=P1+P
理想气体混合时,由于分子间无相互作用, 故碰撞器壁产生的压力,与独立存在时是相同的。 亦即在混合气体中,组分气体是各自独立的