
第六章检测 一、选择题(每小题4分,共32分) 1.若一个多边形的内角和与外角和之和为2520°,则这个多边形的对角线条数为() A.54 B.108 C.77 D.154 2.如图,ABCD的对角线AC,BD相交于点O,E是AB的中点,且AE+EO=4,则ABCD的周长 为) B A.20 B.16 C.12 D.8 3.如图,在△ABC中.∠A=40°AB=AC,点D在边AC上,以CB.CD为边作BCDE.则∠E的度 数为( A.40° B.50° C.60° D.70° 4.如图,四边形ABCD是平行四边形,以点A为圆心、AB的长为半径画弧交AD于点F,再分 别以点B,F为圆心、大于BF的长为半径画弧,两弧交于点M,作射线AM交BC于点E,连接 EF下列结论中不一定成立的是( VM A.BE=EF B.EF∥CD C.AE平分∠BEFD.AB=AE 5.如图,吴伯伯家有一块等边三角形的空地ABC,己知点E,F分别是边AB,AC的中点,量得 EF=5米,他想把四边形BC℉E用篱笆围成一圈放养小鸡,则需用篱笆的长是(). B C A.15米 B.20米 C.25米 D.30米 6.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10, 则四边形ABCD的面积为(). A.6 B.12 C.20 D.24 7.在ABCD中,∠A的平分线把边BC分成长度是3和4的两部分,则ABCD的周长是(). A.22 B.20 C.22或20D.18 8.如图,在四边形ABCD中,AC-4cm,BD=4.5cm,点E,F,G,H分别是边AB,BC,CD,DA的中点, 则四边形EFGH的周长为() A.8.5 cm B.4 cm C.4.5 cm D.17cm 二、填空题(每小题4分,共24分)
第六章检测 一、选择题(每小题 4 分,共 32 分) 1.若一个多边形的内角和与外角和之和为 2 520°,则这个多边形的对角线条数为( ). A.54 B.108 C.77 D.154 2.如图,▱ABCD 的对角线 AC,BD 相交于点 O,E 是 AB 的中点,且 AE+EO=4,则▱ABCD 的周长 为( ). A.20 B.16 C.12 D.8 3.如图,在△ABC 中,∠A=40°,AB=AC,点 D 在边 AC 上,以 CB,CD 为边作▱BCDE,则∠E 的度 数为( ). A.40° B.50° C.60° D.70° 4.如图,四边形 ABCD 是平行四边形,以点 A 为圆心、AB 的长为半径画弧交 AD 于点 F,再分 别以点 B,F 为圆心、大于1 2 BF 的长为半径画弧,两弧交于点 M,作射线 AM 交 BC 于点 E,连接 EF.下列结论中不一定成立的是( ). A.BE=EF B.EF∥CD C.AE 平分∠BEFD.AB=AE 5.如图,吴伯伯家有一块等边三角形的空地 ABC,已知点 E,F 分别是边 AB,AC 的中点,量得 EF=5 米,他想把四边形 BCFE 用篱笆围成一圈放养小鸡,则需用篱笆的长是( ). A.15 米 B.20 米 C.25 米 D.30 米 6.如图,在四边形 ABCD 中,对角线 AC,BD 相交于点 E,∠CBD=90°,BC=4,BE=ED=3,AC=10, 则四边形 ABCD 的面积为( ). A.6 B.12 C.20 D.24 7.在▱ABCD 中,∠A 的平分线把边 BC 分成长度是 3 和 4 的两部分,则▱ABCD 的周长是( ). A.22 B.20 C.22 或 20 D.18 8.如图,在四边形 ABCD 中,AC=4 cm,BD=4.5 cm,点 E,F,G,H 分别是边 AB,BC,CD,DA 的中点, 则四边形 EFGH 的周长为( ). A.8.5 cm B.4 cm C.4.5 cm D.17 cm 二、填空题(每小题 4 分,共 24 分)
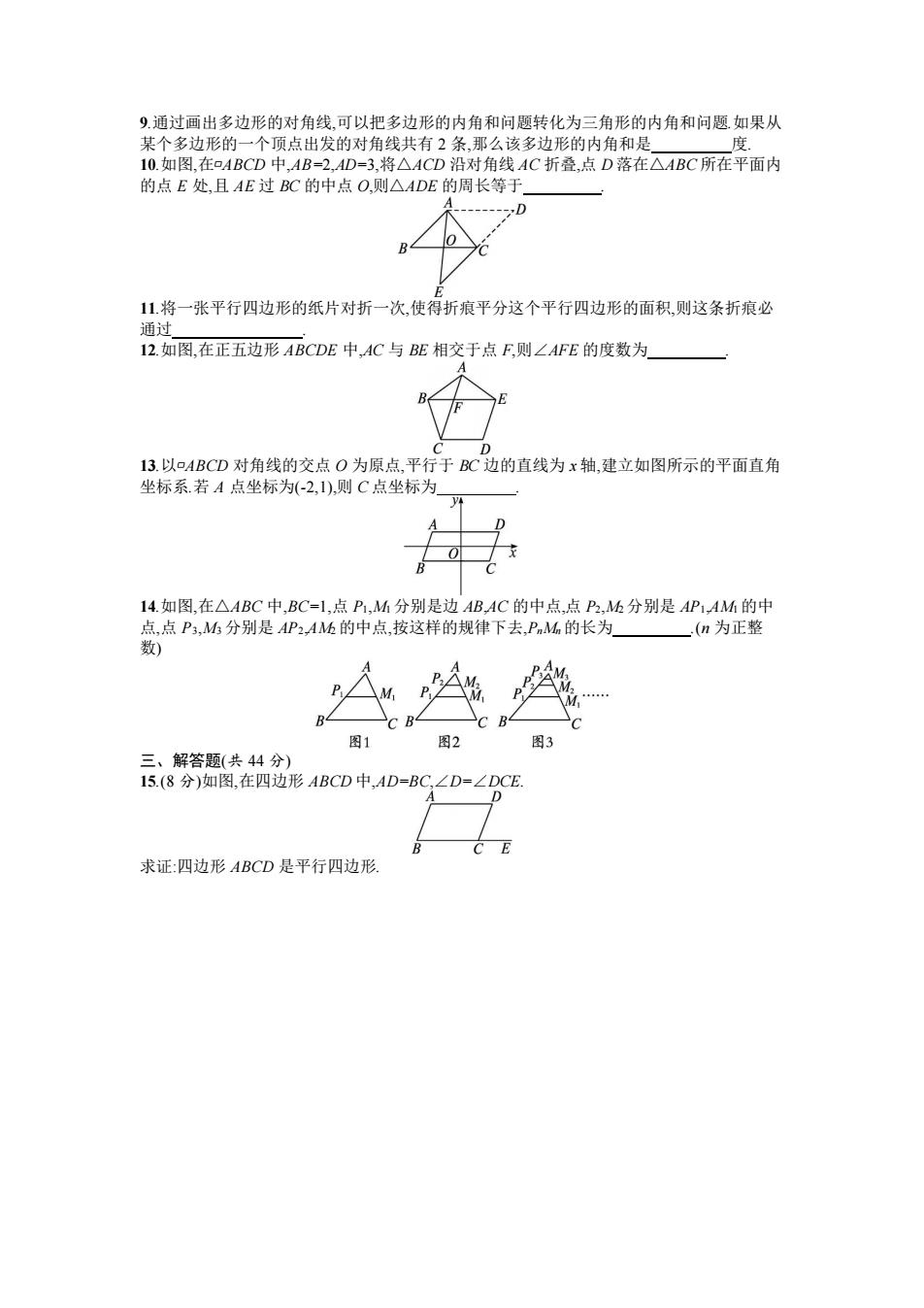
9.通过画出多边形的对角线,可以把多边形的内角和问题转化为三角形的内角和问题如果从 某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是 度. 10.如图,在ABCD中,AB=2,AD=3,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内 的点E处,且AE过BC的中点O,则△ADE的周长等于 D B 11.将一张平行四边形的纸片对折一次,使得折痕平分这个平行四边形的面积,则这条折痕必 通过 12.如图.在正五边形ABCDE中,AC与BE相交于点F则∠AFE的度数为 13.以口ABCD对角线的交点O为原点,平行于BC边的直线为x轴,建立如图所示的平面直角 坐标系.若A点坐标为(-2,1),则C点坐标为 14.如图,在△ABC中,BC=1,点P1,M分别是边AB,AC的中点,点P,M分别是AP1,AM的中 点,点P3,M分别是AP2,Ah的中点,按这样的规律下去,PnM的长为(n为正整 数) 图 图2 图 三、解答题(共44分) 15.(8分)如图,在四边形ABCD中,AD=BC,∠D=∠DCE 求证:四边形ABCD是平行四边形
9.通过画出多边形的对角线,可以把多边形的内角和问题转化为三角形的内角和问题.如果从 某个多边形的一个顶点出发的对角线共有 2 条,那么该多边形的内角和是 度. 10.如图,在▱ABCD 中,AB=2,AD=3,将△ACD 沿对角线 AC 折叠,点 D 落在△ABC 所在平面内 的点 E 处,且 AE 过 BC 的中点 O,则△ADE 的周长等于 . 11.将一张平行四边形的纸片对折一次,使得折痕平分这个平行四边形的面积,则这条折痕必 通过 . 12.如图,在正五边形 ABCDE 中,AC 与 BE 相交于点 F,则∠AFE 的度数为 . 13.以▱ABCD 对角线的交点 O 为原点,平行于 BC 边的直线为 x 轴,建立如图所示的平面直角 坐标系.若 A 点坐标为(-2,1),则 C 点坐标为 . 14.如图,在△ABC 中,BC=1,点 P1,M1 分别是边 AB,AC 的中点,点 P2,M2 分别是 AP1,AM1 的中 点,点 P3,M3 分别是 AP2,AM2 的中点,按这样的规律下去,PnMn 的长为 .(n 为正整 数) 三、解答题(共 44 分) 15.(8 分)如图,在四边形 ABCD 中,AD=BC,∠D=∠DCE. 求证:四边形 ABCD 是平行四边形

16.(8分)如图,在ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F (I)求证:△ABE≌△DFE, (2)连接BD,AF,试判断四边形ABDF的形状,并证明你的结论. 17.(9分)如图①,用直线m去截△ABC的两边,可得到一个新的多边形BCED:如图②、图 ③、图④所示是一个多边形,你能否用一条直线分别去截这个多边形,使得到的新多边形分别 满足下列条件: (1)新多边形的内角和比原多边形的内角和增加了180°; (2)新多边形的内角和与原多边形的内角和相等: (3)新多边形的内角和比原多边形的内角和减少了180° 若能,请在图中画出符合要求的一条直线;若不能,请说明理由. E 图① 图② 图③ 图④ 18.(9分)如图,四边形ABCD是平行四边形,E,F为对角线AC上两点,连接ED,EB,FD,FB.给出 以下结论:①BE∥DF,②BE=DF,③AE=CF.请你从中选取一个作条件,使∠1=∠2成立,并给出 证明 19.(10分)如图,四边形ABCD为平行四边形,M,N分别从D到A、从B到C运动,速度相 同,E,F分别从A到B、从C到D运动,速度相同.它们之间用橡皮绳连紧 M D B N (1)没有出发时,这两条橡皮绳有何关系? (2)若同时出发,(1)中的结论对这两条橡皮绳还成立吗?为什么?
16.(8 分)如图,在▱ABCD 中,点 E 是 AD 的中点,BE 的延长线与 CD 的延长线相交于点 F. (1)求证:△ABE≌△DFE; (2)连接 BD,AF,试判断四边形 ABDF 的形状,并证明你的结论. 17.(9 分)如图①,用直线 m 去截△ABC 的两边,可得到一个新的多边形 BCED;如图②、图 ③、图④所示是一个多边形,你能否用一条直线分别去截这个多边形,使得到的新多边形分别 满足下列条件: (1)新多边形的内角和比原多边形的内角和增加了 180°; (2)新多边形的内角和与原多边形的内角和相等; (3)新多边形的内角和比原多边形的内角和减少了 180°. 若能,请在图中画出符合要求的一条直线;若不能,请说明理由. 图① 图② 图③ 图④ 18.(9 分)如图,四边形 ABCD 是平行四边形,E,F 为对角线 AC 上两点,连接 ED,EB,FD,FB.给出 以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个作条件,使∠1=∠2 成立,并给出 证明. 19.(10 分)如图,四边形 ABCD 为平行四边形,M,N 分别从 D 到 A、从 B 到 C 运动,速度相 同,E,F 分别从 A 到 B、从 C 到 D 运动,速度相同.它们之间用橡皮绳连紧. (1)没有出发时,这两条橡皮绳有何关系? (2)若同时出发,(1)中的结论对这两条橡皮绳还成立吗?为什么?

第六章检测 一、选择题 1.C2.B3.D4.D5.C6.D7.C 8.A 二、填空题 9.54010.1011.对角线的交点 12.72°13.(2-1)14. 三、解答题 15.证明:'∠D=∠DCE, .:AD∥BC 又:AD=BC, ,:四边形ABCD是平行四边形 16.(1)证明:四边形ABCD是平行四边形, .AB∥CD .:∠BAE=∠EDF,∠ABE=∠DFE :,点E是AD的中点, ..AE=DE. .:△ABE≌△DFE. (2)解四边形ABDF是平行四边形. 证明:由(1)得,AB=DF 又由题意知AB∥DF ,:四边形ABDF是平行四边形 17.解都能画出,如图,其中图②冲的新多边形为ABCDHG,图③冲的新多边形为ABCDF,图④ 中的新多边形为ABCD 图② 图③ 图④ 18.解方法一补充条件:③AE=C℉. 证明:AE=CF,:AF=CE :四边形ABCD是平行四边形 .AB=CD.AB∥CD .:∠BAF=∠DCE. .:△ABF≌△CDE. .:∠1=∠2 方法二补充条件:①BE∥DF 证明:BE∥DF .:∠BEC=∠DFA :∠BEA=∠DFC :四边形ABCD是平行四边形, .AB=CD,AB∥CD. ,·∠BAE=∠DCF .·△ABE≌△CDF ..BE=DF :四边形BFDE是平行四边形 .:DE∥BF .:∠1=∠2 19.解(1)没有出发时,这两条橡皮绳相互平分理由如下:
第六章检测 一、选择题 1.C 2.B 3.D 4.D 5.C 6.D 7.C 8.A 二、填空题 9.540 10.10 11.对角线的交点 12.72° 13.(2,-1) 14. 1 2 𝑛 三、解答题 15.证明 ∵∠D=∠DCE, ∴AD∥BC. 又∵AD=BC, ∴四边形 ABCD 是平行四边形. 16.(1)证明 ∵四边形 ABCD 是平行四边形, ∴AB∥CD. ∴∠BAE=∠EDF,∠ABE=∠DFE. ∵点 E 是 AD 的中点, ∴AE=DE. ∴△ABE≌△DFE. (2)解 四边形 ABDF 是平行四边形. 证明:由(1)得,AB=DF. 又由题意知 AB∥DF, ∴四边形 ABDF 是平行四边形. 17.解 都能画出,如图,其中图②中的新多边形为 ABCDHG;图③中的新多边形为 ABCDF;图④ 中的新多边形为 ABCD. 18.解 方法一补充条件:③AE=CF. 证明:∵AE=CF,∴AF=CE. ∵四边形 ABCD 是平行四边形, ∴AB=CD,AB∥CD. ∴∠BAF=∠DCE. ∴△ABF≌△CDE. ∴∠1=∠2. 方法二补充条件:①BE∥DF. 证明:∵BE∥DF, ∴∠BEC=∠DFA. ∴∠BEA=∠DFC. ∵四边形 ABCD 是平行四边形, ∴AB=CD,AB∥CD. ∴∠BAE=∠DCF. ∴△ABE≌△CDF. ∴BE=DF. ∴四边形 BFDE 是平行四边形. ∴DE∥BF. ∴∠1=∠2. 19.解 (1)没有出发时,这两条橡皮绳相互平分.理由如下:

如图,:四边形ABCD是平行四边形 ..OA=OC.OB=OD. 即EF与MN相互平分 A(E) D(M) B(N)C(F) (2)若同时出发,(1)中的结论对这两条橡皮绳还成立,理由如下: A D 如图,连接EM,EN,FM,FN. ·"四边形ABCD是平行四边形」 .:∠A=∠C,AD=BC 又:M,N分别从D到A、从B到C运动,速度相同,E,F分别从A到B、从C到D运动,速度 相同 ..AE=CF,AM=CN. 在△AEM与△CFN中 :AE=CF,∠A=∠C,AM=CN, .:△AEM≌△CFN(SAS). .:EM=FN. 同理EN=MF ,:四边形ENFM为平行四边形. ,:EF与MN相互平分
如图,∵四边形 ABCD 是平行四边形, ∴OA=OC,OB=OD, 即 EF 与 MN 相互平分. (2)若同时出发,(1)中的结论对这两条橡皮绳还成立.理由如下: 如图,连接 EM,EN,FM,FN. ∵四边形 ABCD 是平行四边形, ∴∠A=∠C,AD=BC. 又∵M,N 分别从 D 到 A、从 B 到 C 运动,速度相同,E,F 分别从 A 到 B、从 C 到 D 运动,速度 相同, ∴AE=CF,AM=CN. 在△AEM 与△CFN 中, ∵AE=CF,∠A=∠C,AM=CN, ∴△AEM≌△CFN(SAS). ∴EM=FN. 同理 EN=MF. ∴四边形 ENFM 为平行四边形. ∴EF 与 MN 相互平分