第1课时 平行四边形的边和角的性质 素能演练提升 1.如图,在ABCD中,MB是∠ABC的平分线,交CD于点M,且MC-2,ABCD的周长是14,则 DM等于() A.1 B.2 C.3 D.4 2.如图,在口ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,若 AB=3,AD=-4,则EF的长是() A.1 B.2 C.2.5 D.3 3.(2022黑龙江大庆中考)如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点E处,若 ∠1=56°,∠2=42°,则∠A的度数为( D 3 B----------小A A.108° B.109° C.110° D.111 4.如图,在平行四边形ABCD中,将△ABC沿着AC所在的直线折叠得到△AB'C,B'C交AD于点 E,连接BD,若∠B=60°,∠ACB=45°,AC=V6,则BD的长是(). A.1 B.V2 C.3 D 2 5.如图,在ABCD中,CE⊥AB于点E若∠1=35°,则∠D= D 6.如图,在ABCD中,点E在AD上,且EC平分∠BED,若∠EBC=30°,BE=10,则ABCD的面 积为 7.如图,将ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F,若∠B=80°,∠ACE=2 ∠ECD,FC=a,FD=b,则ABCD的周长为 Bi-- 8.如图,在平行四边形ABCD中,E,F分别是边BC,AD的中点.求证:∠ABF=∠CDE
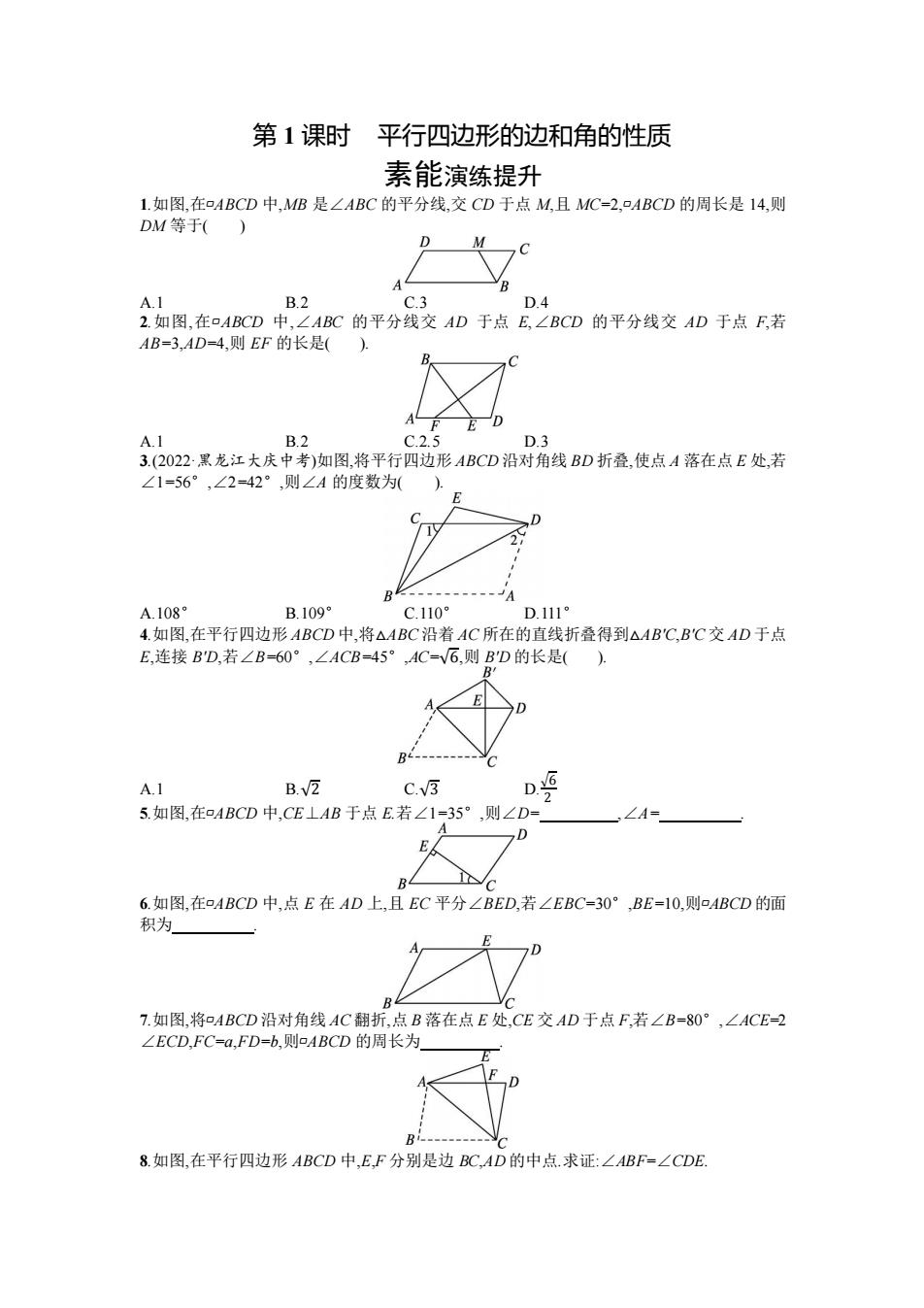
第 1 课时 平行四边形的边和角的性质 素能演练提升 1.如图,在▱ABCD 中,MB 是∠ABC 的平分线,交 CD 于点 M,且 MC=2,▱ABCD 的周长是 14,则 DM 等于( ) A.1 B.2 C.3 D.4 2.如图,在▱ABCD 中,∠ABC 的平分线交 AD 于点 E,∠BCD 的平分线交 AD 于点 F,若 AB=3,AD=4,则 EF 的长是( ). A.1 B.2 C.2.5 D.3 3.(2022·黑龙江大庆中考)如图,将平行四边形 ABCD 沿对角线 BD 折叠,使点 A 落在点 E 处,若 ∠1=56°,∠2=42°,则∠A 的度数为( ). A.108° B.109° C.110° D.111° 4.如图,在平行四边形 ABCD 中,将△ABC 沿着 AC 所在的直线折叠得到△AB'C,B'C 交 AD 于点 E,连接 B'D,若∠B=60°,∠ACB=45°,AC=√6,则 B'D 的长是( ). A.1 B.√2 C.√3 D. √6 2 5.如图,在▱ABCD 中,CE⊥AB 于点 E.若∠1=35°,则∠D= ,∠A= . 6.如图,在▱ABCD 中,点 E 在 AD 上,且 EC 平分∠BED,若∠EBC=30°,BE=10,则▱ABCD 的面 积为 . 7.如图,将▱ABCD 沿对角线 AC 翻折,点 B 落在点 E 处,CE 交 AD 于点 F,若∠B=80°,∠ACE=2 ∠ECD,FC=a,FD=b,则▱ABCD 的周长为 . 8.如图,在平行四边形 ABCD 中,E,F 分别是边 BC,AD 的中点.求证:∠ABF=∠CDE


【素能演练提升】 1.C2.B3.C4.B 5.55°125°6.507.4a+2b 8.证明:四边形ABCD为平行四边形, .AB=CD,AD=BC,∠C=∠A. :E,F分别是边BC,AD的中点, .:CE-BCAF-AD. ..AF=CE. :△ABF≌△CDE(SAS). ,:∠ABF=∠CDE
【素能·演练提升】 1.C 2.B 3.C 4.B 5.55° 125° 6.50 7.4a+2b 8.证明 ∵四边形 ABCD 为平行四边形, ∴AB=CD,AD=BC,∠C=∠A. ∵E,F 分别是边 BC,AD 的中点, ∴CE=1 2 BC,AF=1 2 AD. ∴AF=CE. ∴△ABF≌△CDE(SAS). ∴∠ABF=∠CDE