第三章检测 一、选择题(每小题4分,共32分) 1.(2022·黑龙江牡丹江中考)在下列图形中,既是轴对称图形又是中心对称图形的是(). B D 2.下列图形绕某一点旋转一定角度都能与原图形重合,其中旋转角度最小的是( A.等边三角形B.平行四边形C.正八边形D圆及其一条弦 3.如图,△ABC和△BDE是等边三角形,AB=BD,点A,B,D在一条直线上.由一个三角形变换到 另一个三角形队) A.仅能由平移得到 B.仅能由旋转得到 C.既能由平移得到,也能由旋转得到 D.能由平移得到,但不能由旋转得到 4.在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是() A.(3,0) B.(1,2) C.(5,2) D.(3,4) 5.如图,将△ABC绕点B逆时针旋转a,得到△EBD.若点A恰好在ED的延长线上,则∠CAD 的度数为( A.90°-a B.a C.180°-a D.2a (第5题图) (第6题图) 6.在方格纸中,有标有序号①②③④的4个小正方形,选择其中一个涂黑,与图中阴影部分构成 中心对称图形.该小正方形的序号是( ③ ④ ① ② A.① B.② C.③ D.④ 7.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这 样的图形变换叫滑动对称变换在自然界和日常生活中,存在大量的这种图形变换(如图①)).结 合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图 ②的对应点所具有的性质是( 图 图② A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分
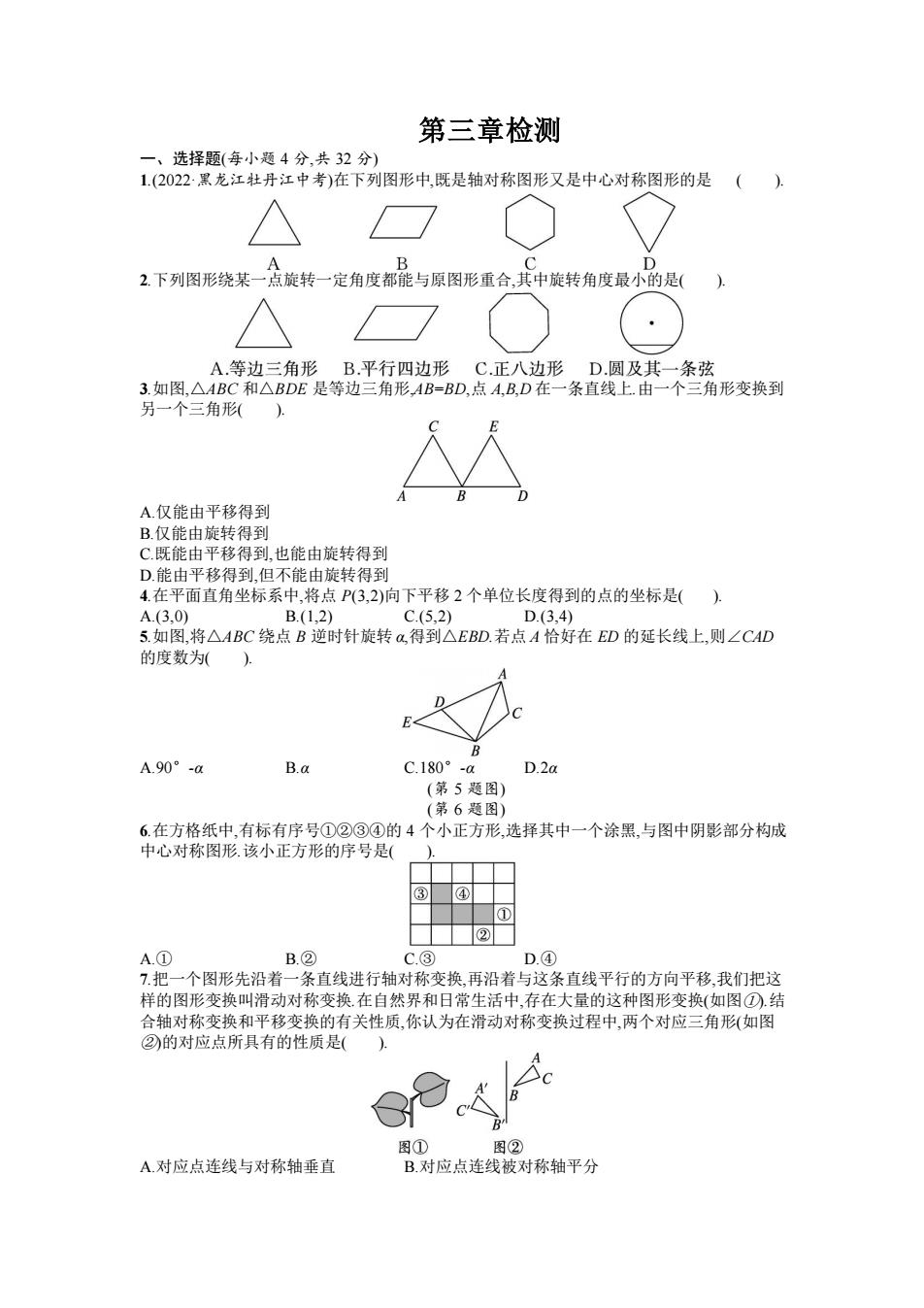
第三章检测 一、选择题(每小题 4 分,共 32 分) 1.(2022·黑龙江牡丹江中考)在下列图形中,既是轴对称图形又是中心对称图形的是 ( ). 2.下列图形绕某一点旋转一定角度都能与原图形重合,其中旋转角度最小的是( ). 3.如图,△ABC 和△BDE 是等边三角形,AB=BD,点 A,B,D 在一条直线上.由一个三角形变换到 另一个三角形( ). A.仅能由平移得到 B.仅能由旋转得到 C.既能由平移得到,也能由旋转得到 D.能由平移得到,但不能由旋转得到 4.在平面直角坐标系中,将点 P(3,2)向下平移 2 个单位长度得到的点的坐标是( ). A.(3,0) B.(1,2) C.(5,2) D.(3,4) 5.如图,将△ABC 绕点 B 逆时针旋转 α,得到△EBD.若点 A 恰好在 ED 的延长线上,则∠CAD 的度数为( ). A.90°-α B.α C.180°-α D.2α (第 5 题图) (第 6 题图) 6.在方格纸中,有标有序号①②③④的 4 个小正方形,选择其中一个涂黑,与图中阴影部分构成 中心对称图形.该小正方形的序号是( ). A.① B.② C.③ D.④ 7.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这 样的图形变换叫滑动对称变换.在自然界和日常生活中,存在大量的这种图形变换(如图①).结 合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图 ②)的对应点所具有的性质是( ). A.对应点连线与对称轴垂直 B.对应点连线被对称轴平分
C对应点连线被对称轴垂直平分D.对应点连线互相平行 8.如图,将△ABC绕点C(0,1)旋转180°得到△A'B'C.设点A的坐标为(a,b),则点A的坐标为 (). A.(-a,-b) B.(-a,-b-1) C.(-a,-b+1) D.(-a,-b+2) 二、填空题(每小题4分,共24分) 9.请写出一个既是轴对称图形,又是中心对称图形的汉字: 10.如图,在等边三角形ABC中,D,E,F分别是边BC,AC,AB的中点,图中的四个小等边三角形 中可以看成是由△FBD平移而得到的三角形是 0 11.用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕 点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角a为 0 T22- 12.如图,已知△ABC与△CDA关于点O对称,过点O任作直线EF分别交AD,BC于点E,F, 下面的结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O,③四 边形ABCD是中心对称图形:④四边形DEOC与四边形BFOA的面积必相等:⑤△AOE与△ COF成中心对称.其中正确的是 (填序号) 10 B 13.如图,正方体的棱长为1cm,将棱A41平移到棱CC的位置上,平移的距离是 D D B 14.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠ D=30°,把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②连接D1B,则∠E1DB的度数 为 图① 图②
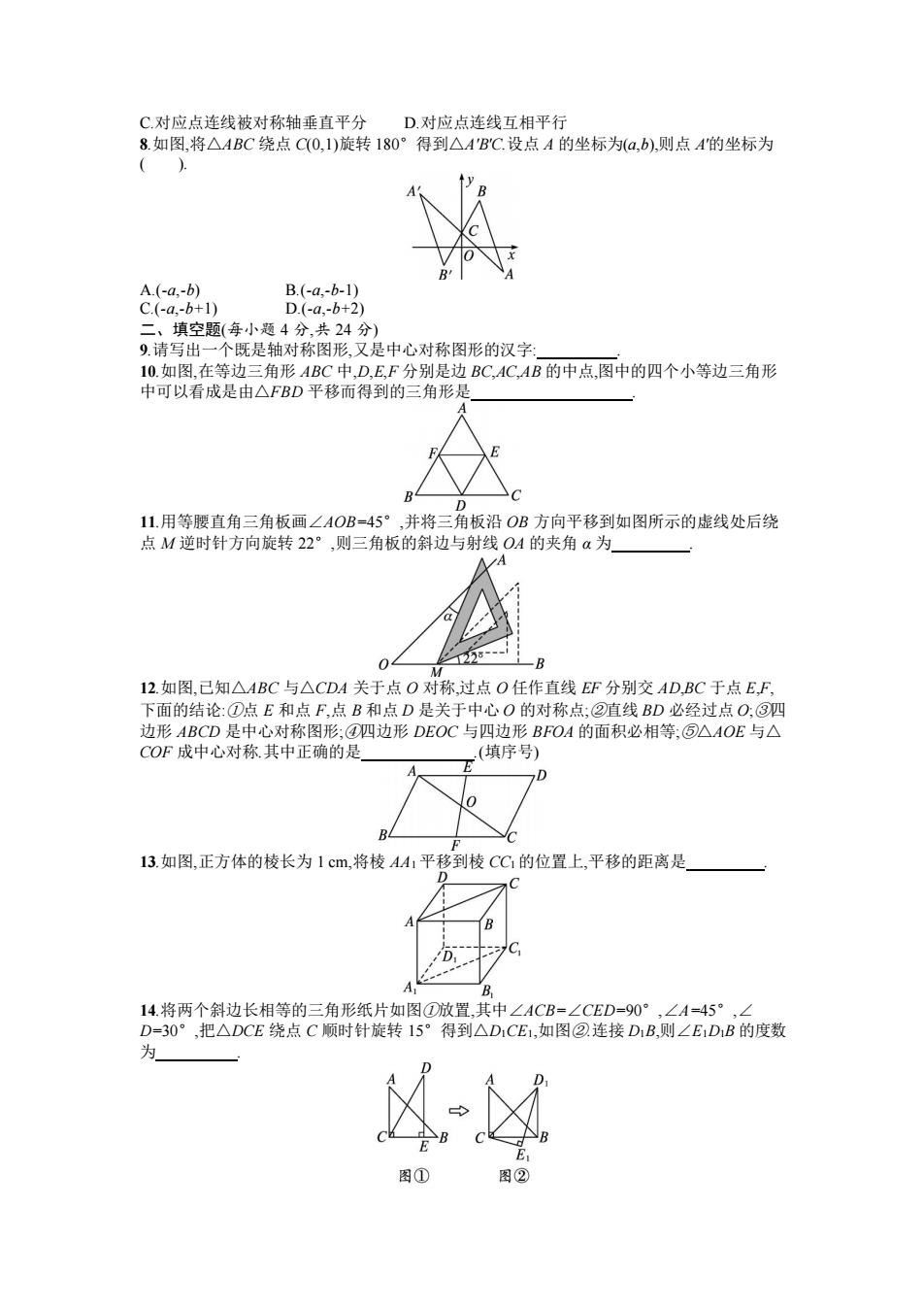
C.对应点连线被对称轴垂直平分 D.对应点连线互相平行 8.如图,将△ABC 绕点 C(0,1)旋转 180°得到△A'B'C.设点 A 的坐标为(a,b),则点 A'的坐标为 ( ). A.(-a,-b) B.(-a,-b-1) C.(-a,-b+1) D.(-a,-b+2) 二、填空题(每小题 4 分,共 24 分) 9.请写出一个既是轴对称图形,又是中心对称图形的汉字: . 10.如图,在等边三角形 ABC 中,D,E,F 分别是边 BC,AC,AB 的中点,图中的四个小等边三角形 中可以看成是由△FBD 平移而得到的三角形是 . 11.用等腰直角三角板画∠AOB=45°,并将三角板沿 OB 方向平移到如图所示的虚线处后绕 点 M 逆时针方向旋转 22°,则三角板的斜边与射线 OA 的夹角 α 为 . 12.如图,已知△ABC 与△CDA 关于点 O 对称,过点 O 任作直线 EF 分别交 AD,BC 于点 E,F, 下面的结论:①点 E 和点 F,点 B 和点 D 是关于中心 O 的对称点;②直线 BD 必经过点 O;③四 边形 ABCD 是中心对称图形;④四边形 DEOC 与四边形 BFOA 的面积必相等;⑤△AOE 与△ COF 成中心对称.其中正确的是 .(填序号) 13.如图,正方体的棱长为 1 cm,将棱 AA1 平移到棱 CC1 的位置上,平移的距离是 . 14.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠ D=30°,把△DCE 绕点 C 顺时针旋转 15°得到△D1CE1,如图②.连接 D1B,则∠E1D1B 的度数 为

三、解答题(共44分) 15.(8分)如图,一个非等腰三角板ABC旋转后到了△AB'C的位置上,其中点B在边AC上 (1)旋转中心是哪一点?(2分) (2)最小旋转角度是多少?并指出此时的旋转方向.(3分) (3)说出∠ABC的对应角与BC的对应线段(3分) 16.(8分)如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的 延长线上的点E重合. (1)三角尺旋转了多少度? (2)连接CD,试判断△CBD的形状 17.(8分)如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系 后,△ABC的顶点均在格点上,点B的坐标为(1,0) (1)画出△ABC关于x轴对称的△A1B1C1: (2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2BzC2, (3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴: (4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标 41 18.(10分)规定:在平面内,如果一个图形绕一个定点旋转一定的角度(0°<a≤180°)后能与 自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转 角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图①),所以 正方形是旋转对称图形,且有两个旋转角. 根据以上规定,回答问题: (1)下列图形是旋转对称图形,但不是中心对称图形的是 A.矩形 B.正五边形C.菱形 D.正六边形 (2)下列三个命题:①冲心对称图形是旋转对称图形:②等腰三角形是旋转对称图形:③圆是旋 转对称图形. 其中真命题的个数为 A.0 B.1 C.2 D.3
三、解答题(共 44 分) 15.(8 分)如图,一个非等腰三角板 ABC 旋转后到了△AB'C'的位置上,其中点 B 在边 AC'上. (1)旋转中心是哪一点?(2 分) (2)最小旋转角度是多少?并指出此时的旋转方向.(3 分) (3)说出∠ABC 的对应角与 BC 的对应线段.(3 分) 16.(8 分)如图,把一个直角三角尺 ACB 绕着 30°角的顶点 B 顺时针旋转,使得点 A 与 CB 的 延长线上的点 E 重合. (1)三角尺旋转了多少度? (2)连接 CD,试判断△CBD 的形状. 17.(8 分)如图,方格纸中的每个小方格都是边长为 1 个单位的正方形,在建立平面直角坐标系 后,△ABC 的顶点均在格点上,点 B 的坐标为(1,0). (1)画出△ABC 关于 x 轴对称的△A1B1C1; (2)画出将△ABC 绕原点 O 按逆时针旋转 90°所得的△A2B2C2; (3)△A1B1C1 与△A2B2C2 成轴对称图形吗?若成轴对称图形,画出所有的对称轴; (4)△A1B1C1 与△A2B2C2 成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标. 18.(10 分)规定:在平面内,如果一个图形绕一个定点旋转一定的角度 α(0°<α≤180°)后能与 自身重合,那么就称这个图形是旋转对称图形,转动的这个角度 α 称为这个图形的一个旋转 角.例如:正方形绕着两条对角线的交点 O 旋转 90°或 180°后,能与自身重合(如图①),所以 正方形是旋转对称图形,且有两个旋转角. 根据以上规定,回答问题: (1)下列图形是旋转对称图形,但不是中心对称图形的是 . A.矩形 B.正五边形 C.菱形 D.正六边形 (2)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋 转对称图形. 其中真命题的个数为 . A.0 B.1 C.2 D.3
(3)图②冲的旋转对称图形是由等腰直角三角形和圆构成的,旋转角有 45°,90°,135°,180°,请将图形补充完整. 图① 图② 19.(10分)如图,己知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10cm, 较小锐角为30°,将这两个三角形摆成如图①所示的形状,使点B,C,F,D在同一条直线上,且 点C与点F重合,将图①中的△ACB绕点C顺时针方向旋转,如图②所示,使点E在边AB 上,AC交DE于点G,求线段FG的长.(保留根号) B D C(F) 图① E G B< D C(F) 图②
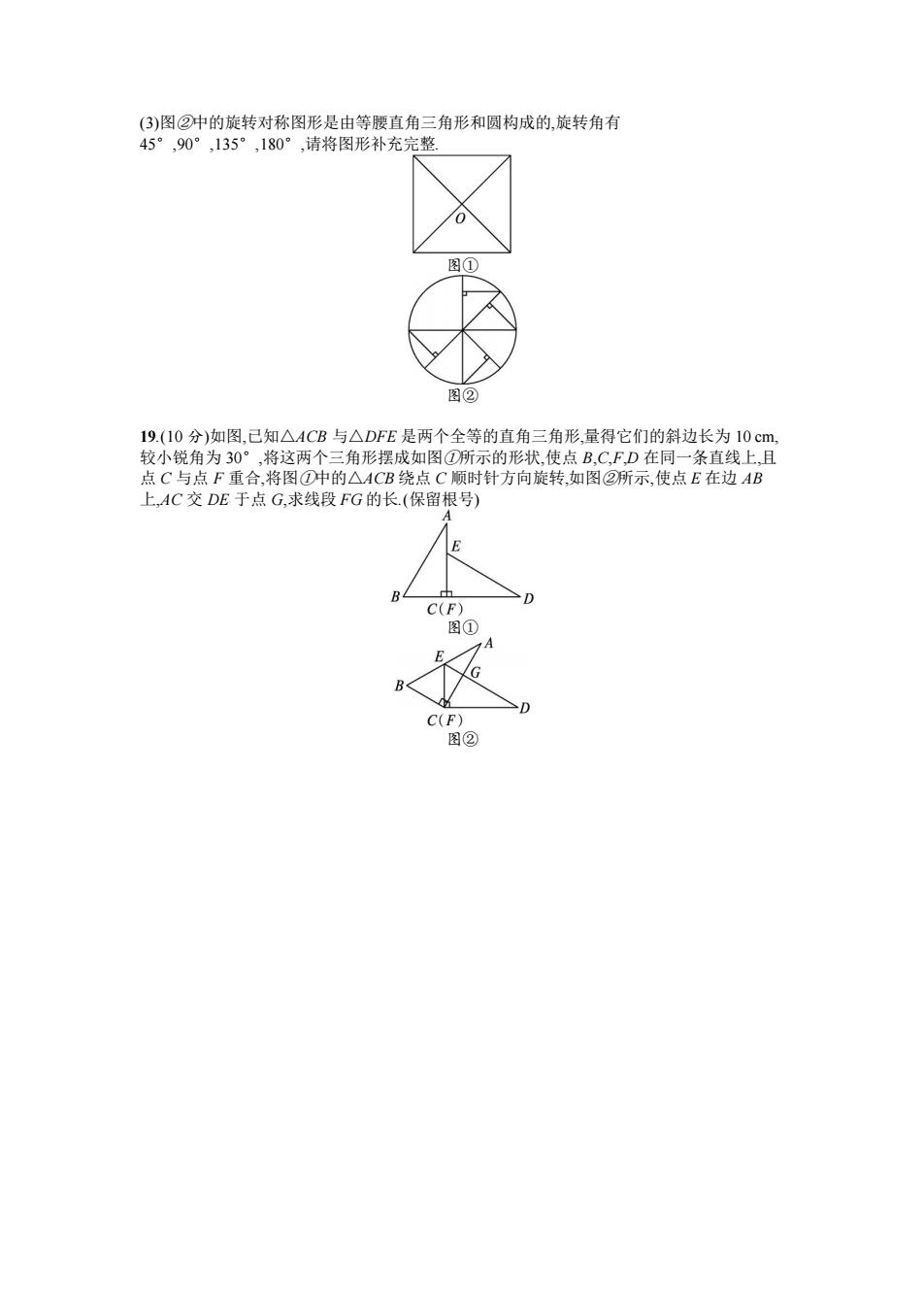
(3)图②中的旋转对称图形是由等腰直角三角形和圆构成的,旋转角有 45°,90°,135°,180°,请将图形补充完整. 图① 图② 19.(10 分)如图,已知△ACB 与△DFE 是两个全等的直角三角形,量得它们的斜边长为 10 cm, 较小锐角为 30°,将这两个三角形摆成如图①所示的形状,使点 B,C,F,D 在同一条直线上,且 点 C 与点 F 重合,将图①中的△ACB 绕点 C 顺时针方向旋转,如图②所示,使点 E 在边 AB 上,AC 交 DE 于点 G,求线段 FG 的长.(保留根号) 图① 图②

第三章检测 一、选择题 1.C2.C3.C4.A5.C6.B7.B 8.D 二、填空题 9.答案不唯一,如一、田等 10.△AFE,△EDC11.22 12.①②③④⑤13.√2cm14.15 三、解答题 15.解(1)旋转中心是点A. (2)最小旋转角度是30°,此时旋转方向为顺时针方向. (3)∠ABC的对应角为∠B,BC的对应线段为B'C: 16.解(1)150°; (2)由CB=BD,可知△CBD是等腰三角形. 17.解(1),(2)如图所示: (3)△A1B1C1与△A2B2C2成轴对称图形,根据轴对称图形的性质画出对称轴即为连接两对应点 的线段,作它的垂直平分线,或连接A1C,A2C2的中点的连线为对称轴. (④)△41B1C与△ABC成中心对称图形,对称中心为线段BB的中点P,坐标是(侵) 18.解(1)是旋转对称图形,但不是中心对称图形的是正五边形,故选B. (2)命题中①③正确,故选C (3)图形如下图所示 19.解:BC=EF,∠B-90°-30°=60°, :△BCE是等边三角形 .:∠AFE=30°. .:∠GFD=60°. 又:‘∠D=∠A=30° .:∠FGD=90°」 在Rt△DEF中,DE=AB=I0cm, .:EF=BC--AB=5 cm. .:DF=VDE2-EFZ=V102-52-5V3(cm). FG-FD-5V3 cp cm
第三章检测 一、选择题 1.C 2.C 3.C 4.A 5.C 6.B 7.B 8.D 二、填空题 9.答案不唯一,如一、田等 10.△AFE,△EDC 11.22° 12.①②③④⑤ 13.√2 cm 14.15° 三、解答题 15.解 (1)旋转中心是点 A. (2)最小旋转角度是 30°,此时旋转方向为顺时针方向. (3)∠ABC 的对应角为∠B',BC 的对应线段为 B'C'. 16.解 (1)150°; (2)由 CB=BD,可知△CBD 是等腰三角形. 17.解 (1),(2)如图所示: (3)△A1B1C1 与△A2B2C2 成轴对称图形,根据轴对称图形的性质画出对称轴即为连接两对应点 的线段,作它的垂直平分线,或连接 A1C1,A2C2 的中点的连线为对称轴. (4)△A1B1C1 与△A2B2C2 成中心对称图形,对称中心为线段 BB2 的中点 P,坐标是( 1 2 , 1 2 ). 18.解 (1)是旋转对称图形,但不是中心对称图形的是正五边形,故选 B. (2)命题中①③正确,故选 C. (3)图形如下图所示. 19.解 ∵BC=EF,∠B=90°-30°=60°, ∴△BCE 是等边三角形. ∴∠AFE=30°. ∴∠GFD=60°. 又∵∠D=∠A=30°, ∴∠FGD=90°. 在 Rt△DEF 中,DE=AB=10 cm, ∴EF=BC=1 2 AB=5 cm. ∴DF=√𝐷𝐸2-𝐸𝐹2=√10 2-5 2=5√3(cm). ∴FG=1 2 FD=5√3 2 cm