第1课时 一元一次不等式与一次函数的关系 素能演练提升 1.要使函数y=(2m-3)x+(3n+1)的图象经过x轴和y轴的正半轴,则m与n的取值范围应为 1 B.m>3,n>-3 Dmn>号 2.已知一次函数y=(2m-1)x的图象上有两点A(1y),B(x2,2).当x12.则m的取值 范围是( A.m2 C.m生 D.m生 3.如图,直线y=+b(k1 4.如图,直线1y=x+1与直线hy=mx+n相交于点P(a,2),则关于x的不等式x+1≥x+n的解 集为 2 12 5.如图,直线y=+b(飞b是常数,0)与直线y=2交于点A(4,2),则关于x的不等式x+b<2的 解集为 y=kx+b —y=2 6.已知过点(0,-2)的直线11=+b(0)与直线22=x+1交于点P(2,m) y (1)写出使得y<2的x的取值范围: (2)求点P的坐标和直线1的解析式
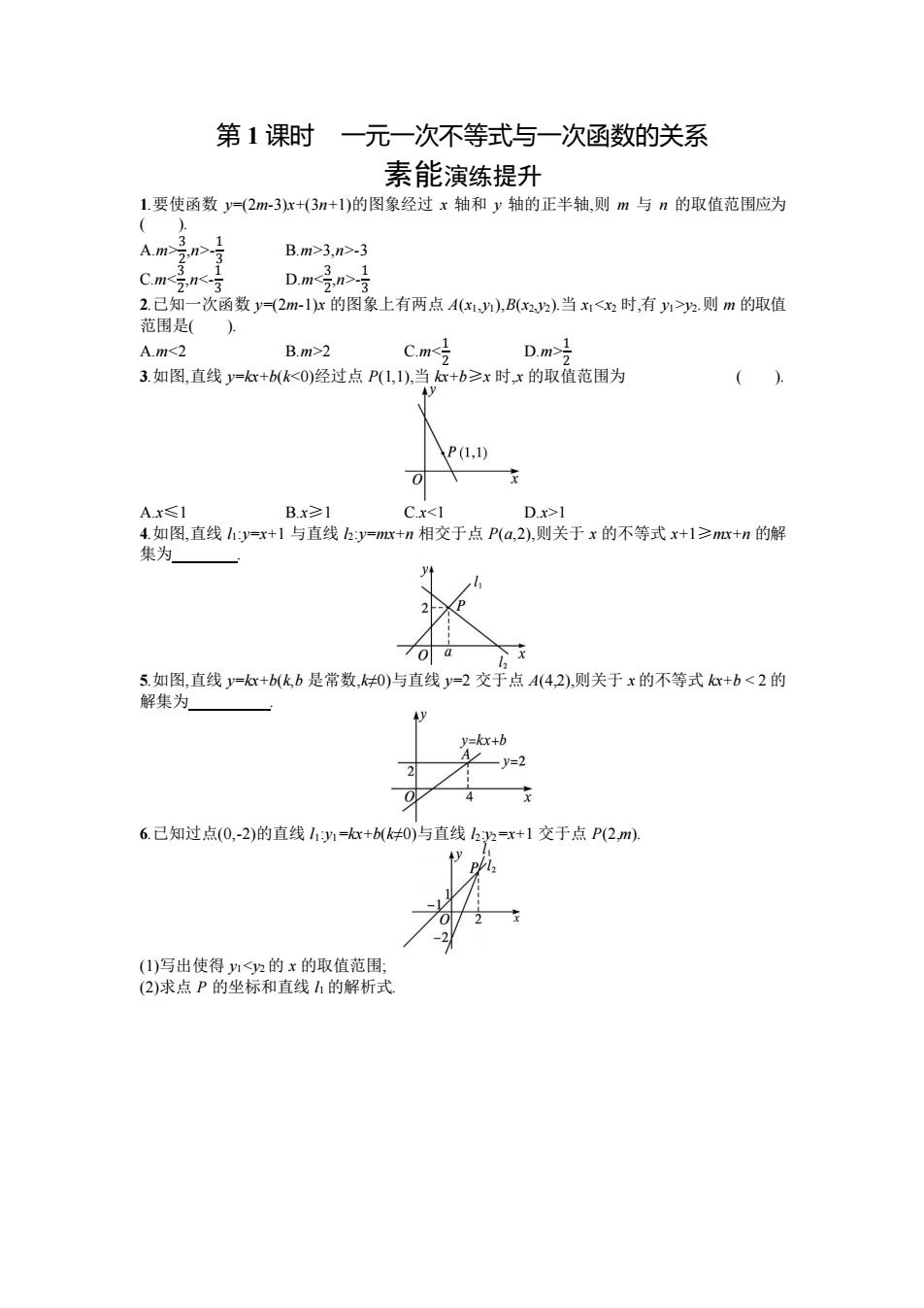
第 1 课时 一元一次不等式与一次函数的关系 素能演练提升 1.要使函数 y=(2m-3)x+(3n+1)的图象经过 x 轴和 y 轴的正半轴,则 m 与 n 的取值范围应为 ( ). A.m>3 2 ,n>- 1 3 B.m>3,n>-3 C.m- 1 3 2.已知一次函数 y=(2m-1)x 的图象上有两点 A(x1,y1),B(x2,y2).当 x1y2.则 m 的取值 范围是( ). A.m2 C.m1 2 3.如图,直线 y=kx+b(k1 4.如图,直线 l1:y=x+1 与直线 l2:y=mx+n 相交于点 P(a,2),则关于 x 的不等式 x+1≥mx+n 的解 集为 . 5.如图,直线 y=kx+b(k,b 是常数,k≠0)与直线 y=2 交于点 A(4,2),则关于 x 的不等式 kx+b < 2 的 解集为 . 6.已知过点(0,-2)的直线 l1:y1=kx+b(k≠0)与直线 l2:y2=x+1 交于点 P(2,m). (1)写出使得 y1<y2 的 x 的取值范围; (2)求点 P 的坐标和直线 l1 的解析式

【素能演练提升】 1D2.C3.A4.x≥15.x<4 6.解(1)根据图象,得当12时,x<2. (2)将点P的坐标代入2=x+1,得m=3. 即P(2,3). 把点P2,3),点(0,-2)的坐标代入=+b,得6_23 解得k= b=-2. 故n会-2
【素能·演练提升】 1.D 2.C 3.A 4.x≥1 5.x<4 6.解 (1)根据图象,得当 y1<y2 时,x<2. (2)将点 P 的坐标代入 y2=x+1,得 m=3. 即 P(2,3). 把点 P(2,3),点(0,-2)的坐标代入 y1=kx+b,得{ 2𝑘 + 𝑏 = 3, 𝑏 = -2, 解得{ 𝑘 = 5 2 , 𝑏 = -2. 故 y1= 5 2 x-2