
第1课时 全等三角形与等腰三角形的性质 素能演练提升 1.如图,已知∠ABC=∠DCB,添加以下条件,不能判定△4BC≌△DCB的是(). A.∠A=∠D B.∠ACB=∠DBC C.AC=DB D.AB=DC 2.(2022湖北荆州中考)如图,直线1∥2,AB=AC,∠BAC-40°,则∠1+∠2的度数是() B -h 2 -l2 A A.60° B.70° C.80° D.90° 3.小明在AB=AC的等腰三角形中,以点B为圆心,BC长为半径画弧交AC于点D,得到如图所 示的图形,则下列结论一定正确的是( ) A.AD=CD B.AD=BD C.∠ABD=∠CBDD.∠BAD=∠CBD 4.如图,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=C,则AD 的长为() A.a+c B.b+c C.a-b+c D.a+b-c 5.在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ ACD=()人 D E B A.16° B.28 C.44° D.45 6.如图,在Rt△4BC中,∠C-90°,AF=EF若∠CFE-72°,则∠B= B E 7.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠ C=36°,则∠DAC的大小为
第 1 课时 全等三角形与等腰三角形的性质 素能演练提升 1.如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB 的是( ). A.∠A=∠D B.∠ACB=∠DBC C.AC=DB D.AB=DC 2.(2022·湖北荆州中考)如图,直线 l1∥l2,AB=AC,∠BAC=40°,则∠1+∠2 的度数是( ). A.60° B.70° C.80° D.90° 3.小明在 AB=AC 的等腰三角形中,以点 B 为圆心,BC 长为半径画弧交 AC 于点 D,得到如图所 示的图形,则下列结论一定正确的是( ). A.AD=CD B.AD=BD C.∠ABD=∠CBD D.∠BAD=∠CBD 4.如图,AB⊥CD,且 AB=CD,E,F 是 AD 上两点,CE⊥AD,BF⊥AD.若 CE=a,BF=b,EF=c,则 AD 的长为( ). A.a+c B.b+c C.a-b+c D.a+b-c 5. 在螳螂的示意图中,AB ∥DE,△ABC 是等腰三角形, ∠ABC=124°, ∠CDE=72°,则∠ ACD=( ). A.16° B.28° C.44° D.45° 6.如图,在 Rt△ABC 中,∠C=90°,AF=EF.若∠CFE=72°,则∠B= . 7.如图,以△ABC 的顶点 B 为圆心,BA 长为半径画弧,交 BC 边于点 D,连接 AD.若∠B=40°,∠ C=36°,则∠DAC 的大小为
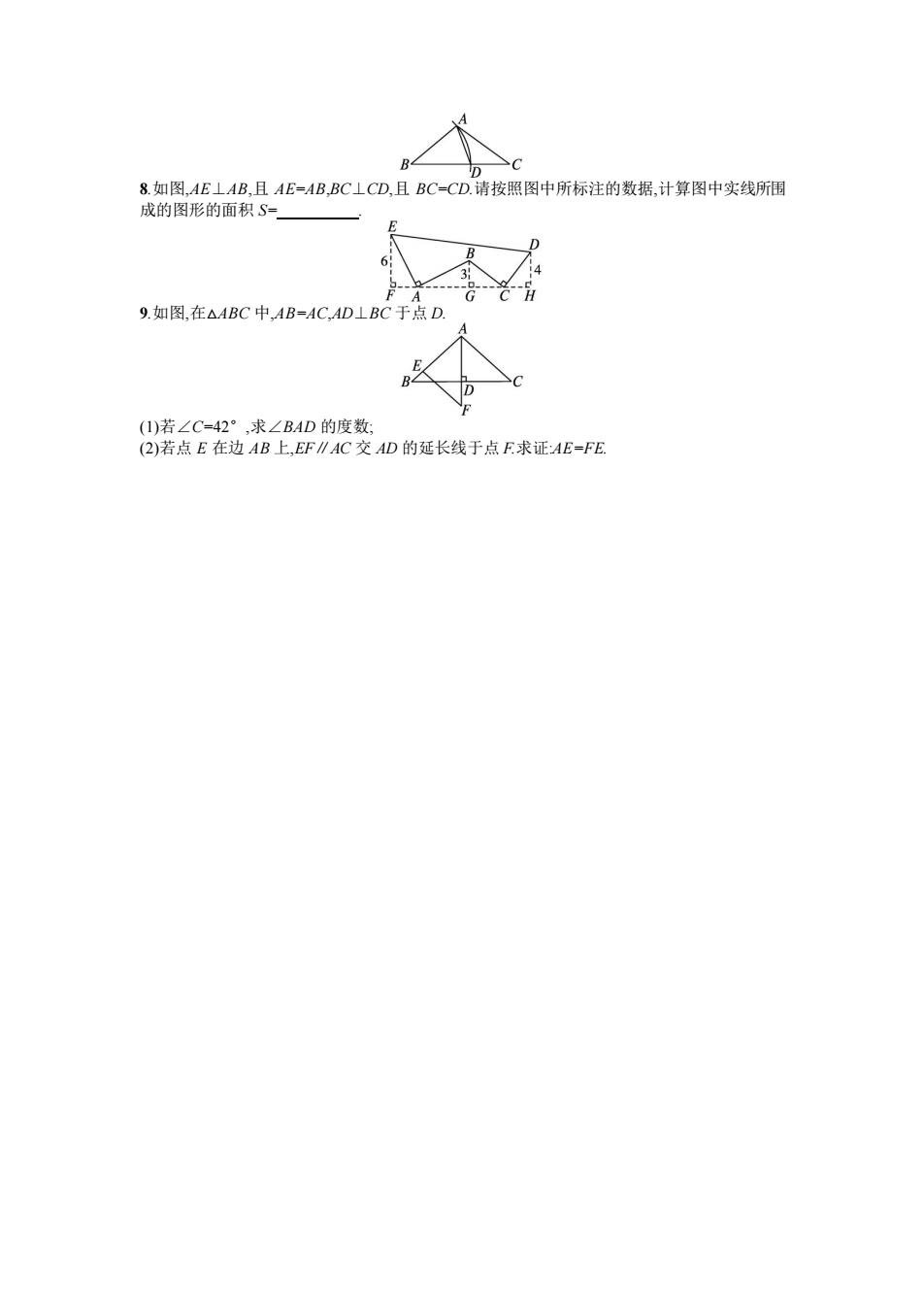
B 8.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD.请按照图中所标注的数据,计算图中实线所围 成的图形的面积S= 9.如图,在△ABC中,AB=AC,AD⊥BC于点D. (1)若∠C=42°,求∠BAD的度数: (2)若点E在边AB上,EF∥AC交AD的延长线于点F求证:AE=FE
8.如图,AE⊥AB,且 AE=AB,BC⊥CD,且 BC=CD.请按照图中所标注的数据,计算图中实线所围 成的图形的面积 S= . 9.如图,在△ABC 中,AB=AC,AD⊥BC 于点 D. (1)若∠C=42°,求∠BAD 的度数; (2)若点 E 在边 AB 上,EF∥AC 交 AD 的延长线于点 F.求证:AE=FE

【素能演练提升】 1.C2.B3.D4.D5.C6.54° 7.34°8.50 9.(1)解AB=AC,AD LBC. .:∠BAD=∠CAD,∠ADC=90° 又∠C=42°,:∠BAD=∠CAD=90°-42°=48°. (2)证明:AB=AC,AD⊥BC, .·∠BAD=∠CAD ·EF∥AC,:∠F=∠CAD, :∠BAD=∠F,:AE=FE
【素能·演练提升】 1.C 2.B 3.D 4.D 5.C 6.54° 7.34° 8.50 9.(1)解 ∵AB=AC,AD⊥BC, ∴∠BAD=∠CAD,∠ADC=90°, 又∠C=42°,∴∠BAD=∠CAD=90°-42°=48°. (2)证明 ∵AB=AC,AD⊥BC, ∴∠BAD=∠CAD. ∵EF∥AC,∴∠F=∠CAD, ∴∠BAD=∠F,∴AE=FE