
第一章检测 一、选择题(每小题4分,共32分) 1.如图,字母A所代表的正方形的面积为(数字表示该正方形的面积)() A.13 B.85 C.8 D.都不对 2.将直角三角形的三边都扩大到原来的3倍,所得的三角形是() A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能 3.已知xy为正数,且x24+02-3)2=0,如果以x,y的长为直角边作一个直角三角形,那么以这个直角三角 形的斜边为边长的正方形的面积为( A.5 B.25 C.7 D.15 4.下列条件中,不能判断一个三角形是直角三角形的是() A.三个角的比为1:2:3 B.三条边满足关系a2=b2-c2 C.三条边的比为1:2:3 D.三个角满足关系∠B+∠C=∠A 5.如图,底面周长为12、高为8的圆柱体上有一只小蚂蚁要从点A爬到点B,则蚂蚁爬行的最短距离是 () A.10 B.8 C.5 D.4 6.分别以下列四组数为一个三角形的三边的长:①6,8,10:②5,12,13:③8,15,17:④7,8,9.其中能构成直角三 角形的有( A.4组 B.3组 C.2组 D.1组 7.△ABC的三边长分别为a,b,c,下列条件:①∠A=∠B-∠C,②∠A:∠B:∠C=3:4:5,③a2=(b+cb-c ④a:b:c=5:12:13,其中能使△ABC是直角三角形的个数为() A.1 B.2 C.3 D.4
第一章检测 一、选择题(每小题 4 分,共 32 分) 1.如图,字母 A 所代表的正方形的面积为(数字表示该正方形的面积)( ). A.13 B.85 C.8 D.都不对 2.将直角三角形的三边都扩大到原来的 3 倍,所得的三角形是( ). A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能 3.已知 x,y 为正数,且|x2 -4|+(y 2 -3)2=0,如果以 x,y 的长为直角边作一个直角三角形,那么以这个直角三角 形的斜边为边长的正方形的面积为( ). A.5 B.25 C.7 D.15 4.下列条件中,不能判断一个三角形是直角三角形的是( ). A.三个角的比为 1∶2∶3 B.三条边满足关系 a 2=b2 -c 2 C.三条边的比为 1∶2∶3 D.三个角满足关系∠B+∠C=∠A 5.如图,底面周长为 12、高为 8 的圆柱体上有一只小蚂蚁要从点 A 爬到点 B,则蚂蚁爬行的最短距离是 ( ). A.10 B.8 C.5 D.4 6.分别以下列四组数为一个三角形的三边的长:①6,8,10;②5,12,13;③8,15,17;④7,8,9.其中能构成直角三 角形的有( ). A.4 组 B.3 组 C.2 组 D.1 组 7.△ABC 的三边长分别为 a,b,c,下列条件:①∠A=∠B-∠C;②∠A∶∠B∶∠C=3∶4∶5;③a 2=(b+c)(b-c); ④a∶b∶c=5∶12∶13,其中能使△ABC 是直角三角形的个数为( ). A.1 B.2 C.3 D.4
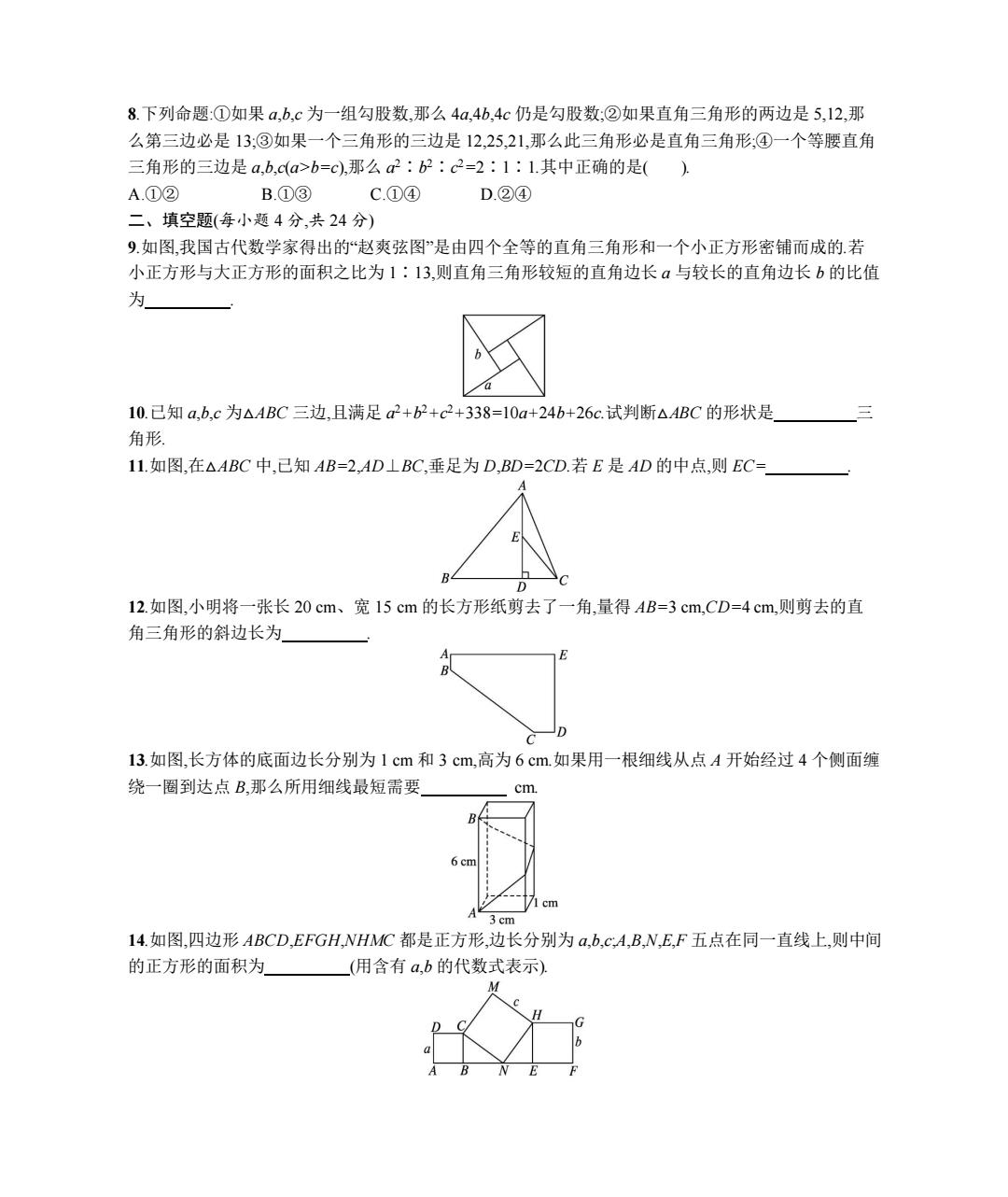
8.下列命题:①如果a,b.c为一组勾股数,那么4a,4b.4c仍是勾股数:②如果直角三角形的两边是5,12,那 么第三边必是13:③如果一个三角形的三边是12,25,21,那么此三角形必是直角三角形:④一个等腰直角 三角形的三边是a,b,c(a>b=c),那么a2:b2:c2-2:1:1.其中正确的是() A.①② B.①③ C.①④ D.②④ 二、填空题(每小题4分,共24分) 9.如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺而成的若 小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边长a与较长的直角边长b的比值 为 10.已知a,b,c为△ABC三边,且满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状是 角形 11.如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC= D 12.如图,小明将一张长20cm、宽15cm的长方形纸剪去了一角,量得AB=3cm,CD=4cm,则剪去的直 角三角形的斜边长为 13.如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠 绕一圈到达点B,那么所用细线最短需要 cm 6 cm /1 cm 3 cm 14.如图,四边形ABCD,EFGH,NHMC都是正方形,边长分别为a,b,c,A,B,N,E,F五点在同一直线上,则中间 的正方形的面积为 (用含有a,b的代数式表示) M
8.下列命题:①如果 a,b,c 为一组勾股数,那么 4a,4b,4c 仍是勾股数;②如果直角三角形的两边是 5,12,那 么第三边必是 13;③如果一个三角形的三边是 12,25,21,那么此三角形必是直角三角形;④一个等腰直角 三角形的三边是 a,b,c(a>b=c),那么 a 2∶b 2∶c 2=2∶1∶1.其中正确的是( ). A.①② B.①③ C.①④ D.②④ 二、填空题(每小题 4 分,共 24 分) 9.如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺而成的.若 小正方形与大正方形的面积之比为 1∶13,则直角三角形较短的直角边长 a 与较长的直角边长 b 的比值 为 . 10.已知 a,b,c 为△ABC 三边,且满足 a 2+b2+c2+338=10a+24b+26c.试判断△ABC 的形状是 三 角形. 11.如图,在△ABC 中,已知 AB=2,AD⊥BC,垂足为 D,BD=2CD.若 E 是 AD 的中点,则 EC= . 12.如图,小明将一张长 20 cm、宽 15 cm 的长方形纸剪去了一角,量得 AB=3 cm,CD=4 cm,则剪去的直 角三角形的斜边长为 . 13.如图,长方体的底面边长分别为 1 cm 和 3 cm,高为 6 cm.如果用一根细线从点 A 开始经过 4 个侧面缠 绕一圈到达点 B,那么所用细线最短需要 cm. 14.如图,四边形 ABCD,EFGH,NHMC 都是正方形,边长分别为 a,b,c;A,B,N,E,F 五点在同一直线上,则中间 的正方形的面积为 (用含有 a,b 的代数式表示)

三、解答题(共44分) 15.(6分)小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面可透过阳光,不计墙的厚度,请计算 阳光透过的最大面积. 20m 16.(8分)如图,在△ABC中,AB=13,BC=14,AC=15,求BC边上的高AD. 17.(8分)在一棵树10m高的B处有两只猴子,一只猴子爬下树走到离树20m处的池塘A处.另一只爬 到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求树高 A① 18.(10分)如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且AB⊥BC.试说明AC⊥CD的理由, 19.(12分)如图,在RtAABC中,∠C=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为ts P -B 备用图1 B∠ 备用图2 (1)求BC边的长, (2)当△ABP为直角三角形时,求t的值;
三、解答题(共 44 分) 15.(6 分)小李准备建一个蔬菜大棚,棚宽 4 m,高 3 m,长 20 m,棚的斜面可透过阳光,不计墙的厚度,请计算 阳光透过的最大面积. 16.(8 分)如图,在△ABC 中,AB=13,BC=14,AC=15,求 BC 边上的高 AD. 17.(8 分)在一棵树 10 m 高的 B 处有两只猴子,一只猴子爬下树走到离树 20 m 处的池塘 A 处.另一只爬 到树顶 D 后直接跃到 A 处,距离以直线计算,如果两只猴子所经过的距离相等,求树高. 18.(10 分)如图,在四边形 ABCD 中,AB=1,BC=2,CD=2,AD=3,且 AB⊥BC.试说明 AC⊥CD 的理由. 19.(12 分)如图,在 Rt△ABC 中,∠C=90°,AB=10 cm,AC=6 cm,动点 P 从点 B 出发沿射线 BC 以 2 cm/s 的速度移动,设运动的时间为 t s. 备用图 1 备用图 2 (1)求 BC 边的长; (2)当△ABP 为直角三角形时,求 t 的值;

(3)当△ABP为等腰三角形时,求t的值 答案: 一、选择题 1.A2.B3.C4.C5.A6.B7.C8.C 二、填空题 9号10.直角 11.112.20cm13.1014.a2+b2 三、解答题 15.100m216.AD=12 17.树高为15m 18.略 19.(1)BC=8cm 2=4或1-9 (3)=5或=8或=2约 8
(3)当△ABP 为等腰三角形时,求 t 的值. 答案: 一、选择题 1.A 2.B 3.C 4.C 5.A 6.B 7.C 8.C 二、填空题 9. 2 3 10.直角 11.1 12.20 cm 13.10 14.a 2+b2 三、解答题 15.100 m2 16.AD=12 17.树高为 15 m. 18.略 19.(1)BC=8 cm (2)t=4 或 t= 25 4 (3)t=5 或 t=8 或 t= 25 8