
期末检测 一、选择题(每小题3分,共30分) 1.在下面四幅图案中,能通过左面的图案平移得到的是( ● A B C D 2.多边形的内角和不可能为( A.180° B.540° C.1080 D.1200° 3.以下是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲体重的取值范围在数轴上表示正确 的是(). 乙40kg甲 甲个 4050+ 丙50kgA 4050 B C D 4.如图,∠AOB=60°,以点O为圆心,以任意长为半径作弧交OA,OB于C,D两点;分别以C,D为圆心 以大于CD的长为半径作弧,两弧相交于点P,以O为端点作射线OP,在射线OP上截取OM=6,则点 M到OB的距离为( ) D A.6 B.2 C3 D.33 5.学校为创建“书香校园”,购买了一批图书,己知购买科普类图书花费10000元,购买文学类图书花费 9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书 的数量比购买文学类图书的数量少100本,求科普类图书平均每本的价格是多少元?若设科普类图书 平均每本的价格是x元,则可列方程为( A1000-9000-100 B9000-10000-=100 x-5 x-5 c.10000_-9000-100 D9000_10000-=100 x-5 X x-5 6.在PABCD中,若∠BAD与∠CDA的平分线交于点E,则△AED的形状是(). A锐角三角形 B.直角三角形C钝角三角形D.不能确定 7.在实数范围内,因式分解16x35x的结果是() A.x16x2.-5) B.x(16x+V5)16x-V5) C.(4x+V5)(4x-V5)D.x4x+V5)(4x-V5) 8.如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,且使点C落在线段AB上的 点E处,点B落在点D处,则B,D两点间的距离为()
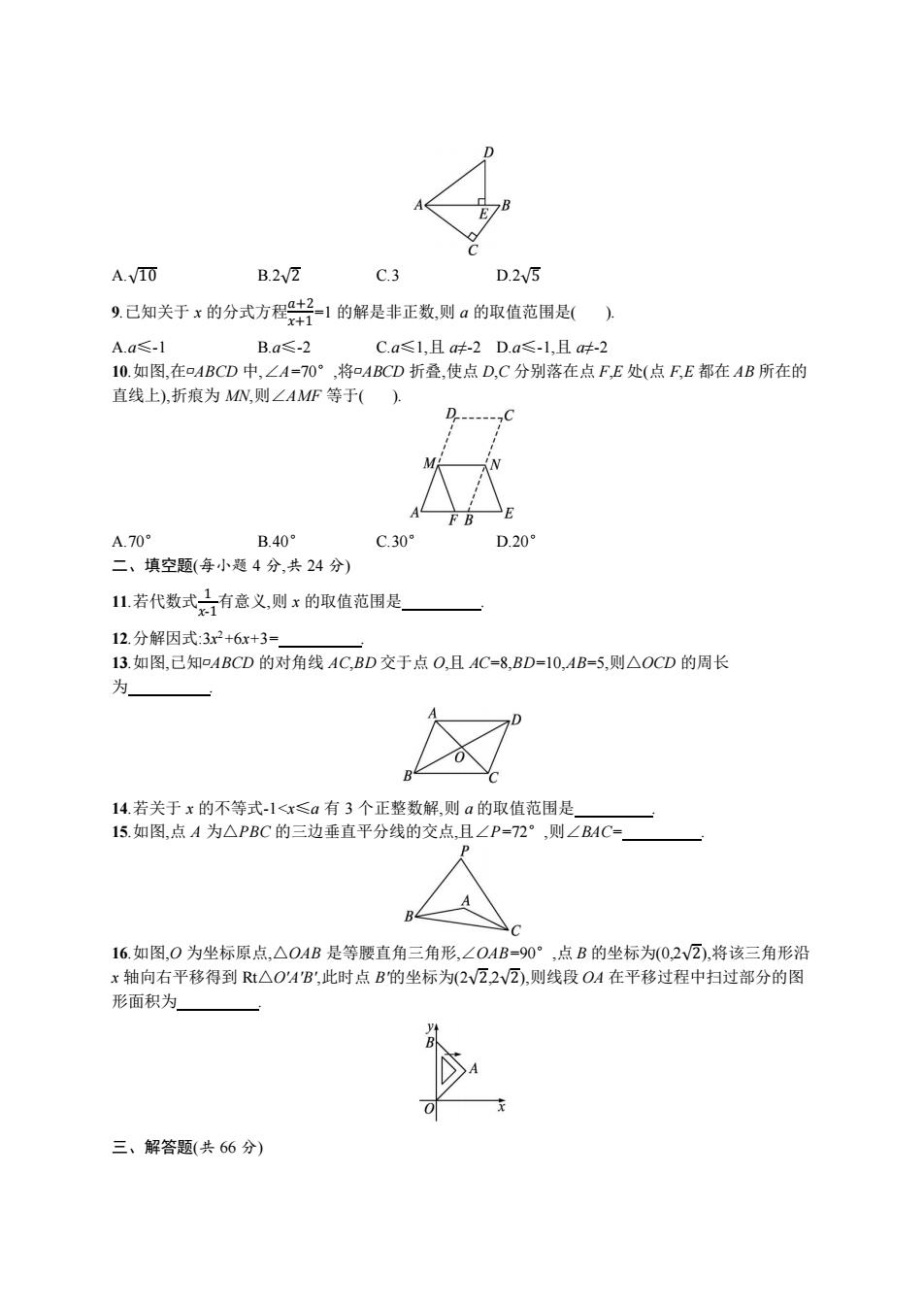
期末检测 一、选择题(每小题 3 分,共 30 分) 1.在下面四幅图案中,能通过左面的图案平移得到的是( ). 2.多边形的内角和不可能为( ). A.180° B.540° C.1 080° D.1 200° 3.以下是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲体重的取值范围在数轴上表示正确 的是( ). 4.如图,∠AOB=60°,以点 O 为圆心,以任意长为半径作弧交 OA,OB 于 C,D 两点;分别以 C,D 为圆心, 以大于1 2 CD 的长为半径作弧,两弧相交于点 P;以 O 为端点作射线 OP,在射线 OP 上截取 OM=6,则点 M 到 OB 的距离为( ). A.6 B.2 C.3 D.3√3 5.学校为创建“书香校园”,购买了一批图书,已知购买科普类图书花费 10 000 元,购买文学类图书花费 9 000 元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵 5 元,且购买科普类图书 的数量比购买文学类图书的数量少 100 本.求科普类图书平均每本的价格是多少元?若设科普类图书 平均每本的价格是 x 元,则可列方程为( ). A. 1 000 𝑥 − 9 000 𝑥-5 =100 B. 9 000 𝑥-5 − 10 000 𝑥 =100 C. 10 000 𝑥-5 − 9 000 𝑥 =100 D. 9 000 𝑥 − 10 000 𝑥-5 =100 6.在▱ABCD 中,若∠BAD 与∠CDA 的平分线交于点 E,则△AED 的形状是( ). A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定 7.在实数范围内,因式分解 16x 3 -5x 的结果是( ). A.x(16x 2 -5) B.x(16x+√5)(16x-√5) C.(4x+√5)(4x-√5) D.x(4x+√5)(4x-√5) 8.如图,在△ABC 中,∠C=90°,AC=4,BC=3,将△ABC 绕点 A 逆时针旋转,且使点 C 落在线段 AB 上的 点 E 处,点 B 落在点 D 处,则 B,D 两点间的距离为( )
A.V1⑩ B.2vZ C.3 D.25 9.已知关于x的分式方程好1的解是非正数则a的取值范围是(人 A.a≤-1 B.a≤-2 C.a≤1,且at-2D.a≤-l,且at-2 10.如图,在ABCD中,∠A=70°,将ABCD折叠,使点D,C分别落在点F,E处(点F,E都在AB所在的 直线上),折痕为MN,则∠AMF等于( D B A.70° B.40° C.30° D.20 二、填空题(每小题4分,共24分) 山,若代数式行有意义,则x的取值范围是 12.分解因式:3x2+6x+3= 13.如图,已知口ABCD的对角线AC,BD交于点O,且AC-8,BD=10,AB=5,则△OCD的周长 为 14.若关于x的不等式-1<x≤a有3个正整数解,则a的取值范围是 15.如图,点A为△PBC的三边垂直平分线的交点,且∠P-72°,则∠BAC= B 16.如图,O为坐标原点,△OAB是等腰直角三角形,∠OAB=90°,点B的坐标为(0,2V2),将该三角形沿 x轴向右平移得到Rt△O'A'B',此时点B的坐标为(2V2,2V2,则线段OA在平移过程中扫过部分的图 形面积为 三、解答题(共66分)
A.√10 B.2√2 C.3 D.2√5 9.已知关于 x 的分式方程𝑎+2 𝑥+1 =1 的解是非正数,则 a 的取值范围是( ). A.a≤-1 B.a≤-2 C.a≤1,且 a≠-2 D.a≤-1,且 a≠-2 10.如图,在▱ABCD 中,∠A=70°,将▱ABCD 折叠,使点 D,C 分别落在点 F,E 处(点 F,E 都在 AB 所在的 直线上),折痕为 MN,则∠AMF 等于( ). A.70° B.40° C.30° D.20° 二、填空题(每小题 4 分,共 24 分) 11.若代数式 1 𝑥-1有意义,则 x 的取值范围是 . 12.分解因式:3x 2+6x+3= . 13.如图,已知▱ABCD 的对角线 AC,BD 交于点 O,且 AC=8,BD=10,AB=5,则△OCD 的周长 为 . 14.若关于 x 的不等式-1<x≤a 有 3 个正整数解,则 a 的取值范围是 . 15.如图,点 A 为△PBC 的三边垂直平分线的交点,且∠P=72°,则∠BAC= . 16.如图,O 为坐标原点,△OAB 是等腰直角三角形,∠OAB=90°,点 B 的坐标为(0,2√2),将该三角形沿 x 轴向右平移得到 Rt△O'A'B',此时点 B'的坐标为(2√2,2√2),则线段 OA 在平移过程中扫过部分的图 形面积为 . 三、解答题(共 66 分)

17.(8分)1)因式分解:m2(m-1)4(1-m2). (2)解方程本-1, 18(8分)先化简(1+)÷再从不等式组经2年 3x<2x+4 的整数解中选一个合适的x的值代入 求值 19.(8分)如图,己知△ABC为等边三角形,BD为△ABC的中线,延长BC至点E,使CE=CD=1,连接 DE,求DE的长. 20.(8分)在如图所示的方格纸中,每个小正方形的边长都为1,△ABC与△A1B1C1构成的图形是中心 对称图形 D (1)画出此中心对称图形的对称中心O,(2分) (2)画出将△A1B1C沿直线DE方向向上平移5格得到的△4B2C2:(3分) (3)要使△42B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转多少度?(直接写出 答案)(3分)
17.(8 分)(1)因式分解:m2 (m-1)-4(1-m2 ). (2)解方程 𝑥 𝑥+3 − 1 𝑥 =1. 18.(8 分)先化简(1 + 2 𝑥-3 ) ÷ 𝑥 2 -1 𝑥 2 -6𝑥+9 ,再从不等式组{ -2𝑥 < 4, 3𝑥 < 2𝑥 + 4 的整数解中选一个合适的 x 的值代入 求值. 19.(8 分)如图,已知△ABC 为等边三角形,BD 为△ABC 的中线,延长 BC 至点 E,使 CE=CD=1,连接 DE,求 DE 的长. 20.(8 分)在如图所示的方格纸中,每个小正方形的边长都为 1,△ABC 与△A1B1C1 构成的图形是中心 对称图形. (1)画出此中心对称图形的对称中心 O;(2 分) (2)画出将△A1B1C1 沿直线 DE 方向向上平移 5 格得到的△A2B2C2;(3 分) (3)要使△A2B2C2 与△CC1C2 重合,则△A2B2C2 绕点 C2 顺时针方向旋转,至少要旋转多少度?(直接写出 答案)(3 分)

21.(I0分)如图,在平行四边形ABCD的边AB,CD上截取AF,CE使得AF=CE,连接EF,点M,N是线段 EF上的两点,且EM=FN,连接AN,CM (I)求证:△AFN≌△CEM (2)若∠CMF=107°,∠CEM-72°,求∠NAF的度数 22.(12分)如图,在平行四边形ABCD中,AE是边BC上的高,点F是DE的中点,AB与AG关于AE对 称,AE与AF关于AG对称 B EG (1)求证:△AEF是等边三角形: (2)若AB=2,求△AFD的面积 23.(12分)为了进一步丰富校园活动,学校准备购买一批足球和篮球,已知购买7个足球和5个篮球的 费用相同:购买40个足球和20个篮球共需3400元 (1)求每个足球和篮球各为多少元? (2)如果学校计划购买足球和篮球共80个,总费用不超过4800元,那么最多能买多少个篮球?
21.(10 分)如图,在平行四边形 ABCD 的边 AB,CD 上截取 AF,CE 使得 AF=CE,连接 EF,点 M,N 是线段 EF 上的两点,且 EM=FN,连接 AN,CM. (1)求证:△AFN≌△CEM; (2)若∠CMF=107°,∠CEM=72°,求∠NAF 的度数. 22.(12 分)如图,在平行四边形 ABCD 中,AE 是边 BC 上的高,点 F 是 DE 的中点,AB 与 AG 关于 AE 对 称,AE 与 AF 关于 AG 对称. (1)求证:△AEF 是等边三角形; (2)若 AB=2,求△AFD 的面积. 23.(12 分)为了进一步丰富校园活动,学校准备购买一批足球和篮球,已知购买 7 个足球和 5 个篮球的 费用相同;购买 40 个足球和 20 个篮球共需 3 400 元. (1)求每个足球和篮球各为多少元? (2)如果学校计划购买足球和篮球共 80 个,总费用不超过 4 800 元,那么最多能买多少个篮球?

期末检测 一、选择题 1.A2.D3.C4.C5.B6.B7.D 8.A9.D10.B 二、填空题 11.x≠112.3(x+1)213.14 14.3≤a<415.144°16.4 三、解答题 17.解(1)原式=2(m-1)+4(m+1)(m-1)=(m-1)(m2+4m+4)=(m-1)(m+2)2. 2去分母,得-(红+3)=+3x解得x=星 经检验,当x=时,分母x+3)不为0,所以x=为原分式方程的解. 18解原式3+2× x-3}2 x-3 x.3 X (x+1)(-1x+1 解不等式组 -2x<4,① (3x<2x+4,② 得-2<x<4, :其整数解为-1,0,1,23. :“要使原分式有意义, x可取0,2. 当x0时,原式-3.(或当x=2时,原式=子) 19.解:“△ABC为等边三角形, .:∠ABC=∠ACB=60°AB=BC. :BD为中线, :∠DBC-ZABC=30°. .'CD=CE. .:∠E=∠CDE :'∠E+∠CDE=∠ACB, :∠E-30°=∠DBC. ..BD=DE. :BD是中线, ..AD=DC=1. :“△ABC是等边三角形, .BC=AC=1+1=2,BD⊥AC 在Rt△BDC中,由勾股定理,得BD=V22-12=V3,故DE=BD=V3 20.解(1)如图,BB1,CC1的交点就是对称中心O. (2)如图,△42B2C2即为所求
期末检测 一、选择题 1.A 2.D 3.C 4.C 5.B 6.B 7.D 8.A 9.D 10.B 二、填空题 11.x≠1 12.3(x+1)2 13.14 14.3≤a<4 15.144° 16.4 三、解答题 17.解 (1)原式=m2 (m-1)+4(m+1)(m-1)=(m-1)(m2+4m+4)=(m-1)(m+2)2 . (2)去分母,得 x 2 -(𝑥 + 3)=x2+3x,解得 x=- 3 4 . 经检验,当 x=- 3 4 时,分母 x(x+3)不为 0,所以 x=- 3 4 为原分式方程的解. 18.解 原式= 𝑥-3+2 𝑥-3 × (𝑥-3) 2 (𝑥+1)(𝑥-1) = 𝑥-3 𝑥+1 . 解不等式组{ -2𝑥 < 4,① 3𝑥 < 2𝑥 + 4,② 得-2<x<4, ∴其整数解为-1,0,1,2,3. ∵要使原分式有意义, ∴x 可取 0,2. ∴当 x=0 时,原式=-3.(或当𝑥 = 2 时,原式 = - 1 3 .) 19.解 ∵△ABC 为等边三角形, ∴∠ABC=∠ACB=60°,AB=BC. ∵BD 为中线, ∴∠DBC=1 2∠ABC=30°. ∵CD=CE, ∴∠E=∠CDE. ∵∠E+∠CDE=∠ACB, ∴∠E=30°=∠DBC. ∴BD=DE. ∵BD 是中线, ∴AD=DC=1. ∵△ABC 是等边三角形, ∴BC=AC=1+1=2,BD⊥AC. 在 Rt△BDC 中,由勾股定理,得 BD=√2 2-1 2 = √3,故 DE=BD=√3. 20.解 (1)如图,BB1,CC1 的交点就是对称中心 O. (2)如图,△A2B2C2 即为所求

(3)△A2B2C2绕点C2顺时针方向至少旋转90°,能与△CCC2重合. 21.(1)证明:四边形ABCD是平行四边形, .:AB∥CD. .:∠CEM=∠AFN :'AF-CE.EM=FN. .:△AFN≌△CEM (2)解由∠CMF=107°,∠CEM-72°,而∠CMF=∠CEM+∠ECM, .:∠ECM=∠CMF-∠CEM=107°-72°=35°. 由(1)得△AFN≌△CEM, .:∠NAF=∠ECM=35° :∠NAF的度数是35° 22.(1)证明在平行四边形ABCD中, :AE是边BC上的高, .:∠DAE=∠AEB=90° :“点F是DE的中点 .:.EF=AF. :AE与AF关于AG对称, .AE=AF. .AE=AF=EF :△AEF是等边三角形 (2)解:“△AEF是等边三角形, .:∠EAF=∠AEF-=60°. .:∠EAG=∠EDA=30°. :AB与AG关于AE对称, .:∠BAE=∠EAG=30°. 在Rt△ABE中, 1AB=2, .:BE-74B-1. :AE=V22-1亚=V3. .:DE=2V3..AD=3. Sum$a0s×EAD×xV3x339 23.解(1)设每个足球为x元,每个篮球为y元
(3)△A2B2C2 绕点 C2 顺时针方向至少旋转 90°,能与△CC1C2 重合. 21.(1)证明 ∵四边形 ABCD 是平行四边形, ∴AB∥CD. ∴∠CEM=∠AFN. ∵AF=CE,EM=FN, ∴△AFN≌△CEM. (2)解 由∠CMF=107°,∠CEM=72°,而∠CMF=∠CEM+∠ECM, ∴∠ECM=∠CMF-∠CEM=107°-72°=35°. 由(1)得△AFN≌△CEM, ∴∠NAF=∠ECM=35°. ∴∠NAF 的度数是 35°. 22.(1)证明 在平行四边形 ABCD 中, ∵AE 是边 BC 上的高, ∴∠DAE=∠AEB=90°. ∵点 F 是 DE 的中点, ∴EF=AF. ∵AE 与 AF 关于 AG 对称, ∴AE=AF. ∴AE=AF=EF. ∴△AEF 是等边三角形. (2)解 ∵△AEF 是等边三角形, ∴∠EAF=∠AEF=60°. ∴∠EAG=∠EDA=30°. ∵AB 与 AG 关于 AE 对称, ∴∠BAE=∠EAG=30°. 在 Rt△ABE 中, ∵AB=2, ∴BE=1 2 AB=1. ∴AE=√2 2-1 2 = √3. ∴DE=2√3.∴AD=3. ∴S△AFD= 1 2 S△ADE= 1 2 × 1 2 AE·AD=1 2 × 1 2 × √3×3= 3√3 4 . 23.解 (1)设每个足球为 x 元,每个篮球为 y 元

报据是意46230y=340. 解代二58 故每个足球为50元,每个篮球为70元 (2)设买篮球m个,则买足球(80-m)个. 根据题意得70m+50(80-m)≤4800,解得m≤40. 因为m为整数,所以m最大取40. 故最多能买40个篮球
根据题意得{ 7𝑥 = 5𝑦, 40𝑥 + 20𝑦 = 3 400, 解得{ 𝑥 = 50, 𝑦 = 70. 故每个足球为 50 元,每个篮球为 70 元. (2)设买篮球 m 个,则买足球(80-m)个. 根据题意得 70m+50(80-m)≤4 800,解得 m≤40. 因为 m 为整数,所以 m 最大取 40. 故最多能买 40 个篮球