
第十二章检测 一、选择题(每小题3分,共30分) 1.下列命题中,正确的是(C), A.两条边及一条边的对角对应相等的两个三角形全等 B.两条边相等的两直角三角形全等 C.两个角及第三个角的对边对应相等的两个三角形全等 D.两个角及一边相等的两个三角形全等 2.仔细观察用直尺和圆规作一个角∠A'O'B等于己知角∠AOB的示意图(如图), 根据所学的“全等三角形”这一章的相关知识,则画出∠A'OB'=∠AOB的依据是 (D). A.SAS B.ASA C.AAS D.SSS 3.如图,已知点E在AB上,点D在AC上,且∠B=∠C,则补充下列一个条件后仍无 法判定△ABD≌△ACE的是(B)】 AAE-AD B.∠AEC=∠ADB C.CE=BD D.AB=AC 4.如图,已知△ABC≌△AEF,AB=BC,则下列结论: ①AC=AF ②∠FAB=∠EAB: ③EF=BC, ④∠EAB=∠FAC
第十二章检测 一、选择题 (每小题 3 分,共 30 分) 1.下列命题中,正确的是(C). A.两条边及一条边的对角对应相等的两个三角形全等 B.两条边相等的两直角三角形全等 C.两个角及第三个角的对边对应相等的两个三角形全等 D.两个角及一边相等的两个三角形全等 2.仔细观察用直尺和圆规作一个角∠A'O'B'等于已知角∠AOB 的示意图 (如图), 根据所学的 “全等三角形”这一章的相关知识,则画出∠A'O'B'=∠AOB 的依据是 (D). A.SAS B.ASA C.AAS D.SSS 3.如图,已知点 E 在 AB 上,点 D 在 AC 上,且∠B=∠C,则补充下列一个条件后仍无 法判定△ABD ≌△ACE 的是(B). A.AE=AD B.∠AEC=∠ADB C.CE=BD D.AB=AC 4.如图,已知△ABC ≌△AEF,AB=BC,则下列结论: ①AC=AF; ②∠FAB=∠EAB; ③EF= BC; ④∠EAB=∠FAC

其中正确的结论有(C), A.1个 B.2个 C.3个 D.4个 5.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面 积分别为50和39,则△EDF的面积为B) D A.11 B.5.5 C.7 D.3.5 6.如图,欲测量古塔周围两点A,B间的距离,可延长AO至点C,使CO=AO,延长BO 至点D,使DO=BO,则△COD≌△AOB,从而通过测量CD就可得出A,B间的距离. 则△COD≌△AOB的根据是(A) D∠ A.SAS B.ASA C.AAS D.SSS 7.如图,∠DAC=∠CBD,∠ACD=∠BDC,则下列结论中错误的是(C)
其中正确的结论有 (C). A.1 个 B.2 个 C.3 个 D.4 个 5.如图,AD 是△ABC 的角平分线,DF⊥AB,垂足为 F,DE=DG,△ADG 和△AED 的面 积分别为 50 和 39,则△EDF 的面积为(B). A.11 B.5.5 C.7 D.3.5 6.如图,欲测量古塔周围两点 A,B 间的距离,可延长 AO 至点 C,使 CO=AO,延长 BO 至点 D,使 DO=BO,则△COD≌△AOB,从而通过测量 CD 就可得出 A,B 间的距离. 则△COD ≌△AOB 的根据是(A). A.SAS B.ASA C.AAS D.SSS 7.如图,∠DAC=∠CBD,∠ACD=∠BDC,则下列结论中错误的是(C)

A.△ADC≌△BCD B.△ABD≌△BAC C.△ABD≌△COD D.△AOD≌△BOC 8.在△ABC和△DEF中AB=DEAC=DF,两三角形的高分别为AM,DN,若AM=DN, 则∠C与∠F的关系是(C) A.相等 B.互补 C.相等或互补 D.相等或互余 9.如图,在△ABC中,D,E分别是边AC,BC上的点,若△ADB≌△EDB≌△EDC,则 ∠C的度数为D)】 A.15° B.20° C.25° D.30 10.在如图所示的3×3的正方形网格中,∠1+∠2+∠3+∠4+∠5等于(C) A.145° B.180° C.225° D.270 二、填空题(每小题4分,共24分) 11.如图,已知BD=DC,∠1=∠2,则AB=AC,∠B=∠C
A.△ADC ≌△BCD B.△ABD ≌△BAC C.△ABD ≌△COD D.△AOD ≌△BOC 8.在△ABC 和△DEF 中,AB=DE,AC=DF,两三角形的高分别为 AM,DN,若 AM=DN, 则∠C 与∠F 的关系是(C). A.相等 B.互补 C.相等或互补 D.相等或互余 9.如图,在△ABC 中,D,E 分别是边 AC,BC 上的点,若△ADB ≌△EDB ≌△EDC,则 ∠C 的度数为(D). A.15° B. 20° C. 25° D. 30° 10.在如图所示的 3×3 的正方形网格中,∠1+∠2+∠3+∠4+∠5 等于(C). A.145° B. 180° C. 225° D. 270° 二、填空题 (每小题 4 分,共 24 分) 11.如图,已知 BD=DC,∠1=∠2,则 AB=AC,∠B=∠C

12.如图,己知AC,BD相交于点O,且OA=OB,OC=OD,则图中全等三角形有3对. 13.已知△ABC≌△DEF,△ABC的周长为20cm,AB=5cm,BC=8cm,则FD=Zcm 14.由全等的图形拼成的图案如图所示,其中AD=0.5cm,BC=1cm,则AF=6cm D B 15.如图,在RtAABC中,∠ACB=90°,BC-3cm,CD⊥AB交AB于点D,在AC上取一 点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则AE=2cm 16.如图,已知△ABC的三边AB,BC,CA的长分别为40,50,60.△ABC的三条角平分 线相交于点O,则S△4B0:SaBC0:S△CA0=4:5:6 三、解答题(共96分,写出必要的文字说明、证明过程或演算步骤) 17.(8分)如图,工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器, 只有一个刻度尺.他是这样操作的:①分别在BA和CA上取点E和点G,使BE=CG, ②在BC上取点D和点F,使BD=CF,③量出DE的长为am,FG的长为bm.若a=b, 则说明∠B和∠C是相等的.他的这种做法合理吗?请说明理由
12.如图,已知 AC,BD 相交于点 O,且 OA=OB,OC=OD,则图中全等三角形有 3 对. 13.已知△ABC≌△DEF,△ABC 的周长为 20 cm,AB=5 cm,BC=8 cm,则 FD=7 cm. 14.由全等的图形拼成的图案如图所示,其中 AD=0.5 cm,BC=1 cm,则 AF=6 cm. 15.如图,在 Rt△ABC 中,∠ACB=90°,BC=3 cm,CD⊥AB 交 AB 于点 D,在 AC 上取一 点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5 cm,则AE=2 cm. 16.如图,已知△ABC 的三边 AB,BC,CA 的长分别为 40,50,60.△ABC 的三条角平分 线相交于点 O,则 S△ABO∶S△BCO∶S△CAO=4∶5∶6. 三、解答题 (共 96 分,写出必要的文字说明、证明过程或演算步骤) 17.(8分)如图,工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器, 只有一个刻度尺.他是这样操作的:①分别在 BA 和 CA 上取点 E 和点G,使 BE=CG; ②在 BC 上取点D 和点F,使 BD=CF;③量出 DE 的长为 a m,FG 的长为 b m.若 a=b, 则说明∠B 和∠C 是相等的.他的这种做法合理吗?请说明理由

解:合理理由如下:因为他这样做是利用“SSS证明了△BED≌△CGF, 所以可得∠B=∠C 18.(8分)如图,已知M是线段AB的中点,MC=MD,∠CMA=∠DMB.试证明:AC=BD. 证明:因为M是AB的中点, 所以AM=BM 又MC=MD,∠CMA=∠DMB 所以△AMC≌△BMD(SAS), 所以AC=BD 19.(8分)如图,点A,B,D,E在一条直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF 证明:因为AD=EB, 所以AD-BD=EB-BD, 即AB=ED 因为BC∥DF,所以∠CBD=∠FDB. 所以∠ABC=∠EDF 因为∠C=∠F 所以AABC≌△EDF(AAS) 所以AC=EF 20.(10分)小明和小刚玩跷跷板的示意图如图所示,横板绕它的中点O上下转动 立柱OC与地面垂直.当一方着地时,另一方上升到最高点.问:在上下转动横板的 过程中,两人上升的最大高度AA',BB有何数量关系?请说明理由 解:AA'=BB:理由如下:
解:合理.理由如下:因为他这样做是利用 “SSS”证明了△BED ≌△CGF, 所以可得∠B=∠C. 18.(8分)如图,已知M是线段AB的中点,MC=MD,∠CMA=∠DMB.试证明:AC=BD. 证明:因为 M 是 AB 的中点, 所以 AM=BM. 又 MC=MD,∠CMA=∠DMB, 所以△AMC ≌△BMD (SAS). 所以 AC=BD. 19.(8 分)如图,点 A,B,D,E 在一条直线上,AD=EB,BC∥DF,∠C=∠F.求证:AC=EF. 证明:因为 AD=EB, 所以 AD-BD=EB-BD, 即 AB=ED. 因为 BC∥DF,所以∠CBD=∠FDB. 所以∠ABC=∠EDF. 因为∠C=∠F, 所以△ABC ≌△EDF(AAS). 所以 AC=EF. 20.(10 分)小明和小刚玩跷跷板的示意图如图所示,横板绕它的中点 O 上下转动, 立柱 OC 与地面垂直.当一方着地时,另一方上升到最高点.问:在上下转动横板的 过程中,两人上升的最大高度 AA',BB'有何数量关系?请说明理由. 解:AA'=BB'.理由如下:

因为AA'与BB表示两人上升的最大高度, 所以AA'⊥AB于点A, BB'⊥AB于点B! 所以∠A'AB'=∠BB'A=90° 在Rt△A'AB和Rt△BB'A中, (A'B'=BA, AB'=B'A, 所以Rt△A'AB'≌Rt△BB'A(HL), 所以AA'=BB! 21.(10分)如图,已知AC,BD相交于点O,AB=DC,∠A=∠D (1)请写出5个由已知条件可以推出的结论.(对顶角相等除外,不再添加辅助线) (2)从写出的5个结论中任选一个进行证明 解:(1)(答案不唯一) △AOB≌△DOC,OA=OD,OB=OC,∠ABO=∠DCO, ∠OBC=∠OCB. (2)(答案不唯一,以△AOB≌△DOC为例) 证明△AOB≌△DOC的过程如下: 因为AB=DC,∠A=∠D 又∠AOB=∠DOC, 所以△AOB2△DOC(AAS), 22.(I2分)如图,AC∥BE,点D在BC上,AB=DE,∠ABE=∠CDE. 求证DC=BE-AC 证明:因为AC∥BE
因为 AA'与 BB'表示两人上升的最大高度, 所以 AA'⊥AB'于点 A, BB'⊥AB'于点 B'. 所以∠A'AB'=∠BB'A=90°. 在 Rt△A'AB'和 Rt△BB'A 中, { 𝐴'𝐵'=𝐵𝐴, 𝐴𝐵'=𝐵'𝐴, 所以 Rt△A'AB '≌Rt△BB'A (HL), 所以 AA'=BB'. 21.(10 分)如图,已知 AC,BD 相交于点 O,AB=DC,∠A=∠D. (1) 请写出 5 个由已知条件可以推出的结论.(对顶角相等除外,不再添加辅助线) (2) 从写出的 5 个结论中任选一个进行证明. 解:(1)(答案不唯一) △AOB≌△DOC,OA=OD,OB=OC,∠ABO=∠DCO, ∠OBC=∠OCB. (2)(答案不唯一,以△AOB≌△DOC 为例) 证明△AOB ≌△DOC 的过程如下: 因为 AB=DC,∠A=∠D, 又∠AOB=∠DOC, 所以△AOB ≌△DOC (AAS). 22.(12 分)如图,AC∥BE,点 D 在 BC 上,AB=DE,∠ABE=∠CDE. 求证:DC=BE-AC. 证明:因为 AC∥BE

所以∠C=∠DBE 且∠A+∠ABE=180° 因为∠BDE+∠CDE=180°, ∠ABE=∠CDE, 所以∠A=∠BDE, 在△ABC和△DEB中, (LC =LDBE, LA=LBDE, AB DE, 所以△ABC≌△DEB(AAS)】 所以AC=DB,BC=EB. 因为DC=BC-BD 所以DC=BE-AC 23.(12分)如图,D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且 BM<BN,DM=DN,∠BMD+∠BND=18O°.求证:BD平分∠ABC 证明:如图,过点D作DP⊥AB DQ⊥BC,垂足分别为P,Q. 因为∠BMD+∠BND=180° 而∠BMD+∠PMD=180°, 所以∠BND=∠PMD 在△DPM与△DQN中, (LDPM=∠DQN=90°, ∠PMD=LQND, DM DN, 所以△DPM≌△DON(AAS)】
所以∠C=∠DBE, 且∠A+∠ABE=180°. 因为∠BDE+∠CDE=180°, ∠ABE=∠CDE, 所以∠A=∠BDE. 在△ABC 和△DEB 中, { ∠𝐶 = ∠𝐷𝐵𝐸, ∠𝐴 = ∠𝐵𝐷𝐸, 𝐴𝐵 = 𝐷𝐸, 所以△ABC ≌△DEB (AAS). 所以 AC=DB,BC=EB. 因为 DC=BC-BD, 所以 DC=BE-AC. 23.(12 分)如图,D 为锐角∠ABC 内一点,点 M 在边 BA 上,点 N 在边 BC 上,且 BM<BN,DM=DN,∠BMD+∠BND=180°.求证:BD 平分∠ABC. 证明:如图,过点 D 作 DP⊥AB, DQ⊥BC,垂足分别为 P,Q. 因为∠BMD+∠BND=180°, 而∠BMD+∠PMD=180°, 所以∠BND=∠PMD. 在△DPM 与△DQN 中, { ∠𝐷𝑃𝑀 = ∠𝐷𝑄𝑁 = 90°, ∠𝑃𝑀𝐷 = ∠𝑄𝑁𝐷, 𝐷𝑀 = 𝐷𝑁, 所以△DPM ≌△DQN (AAS)
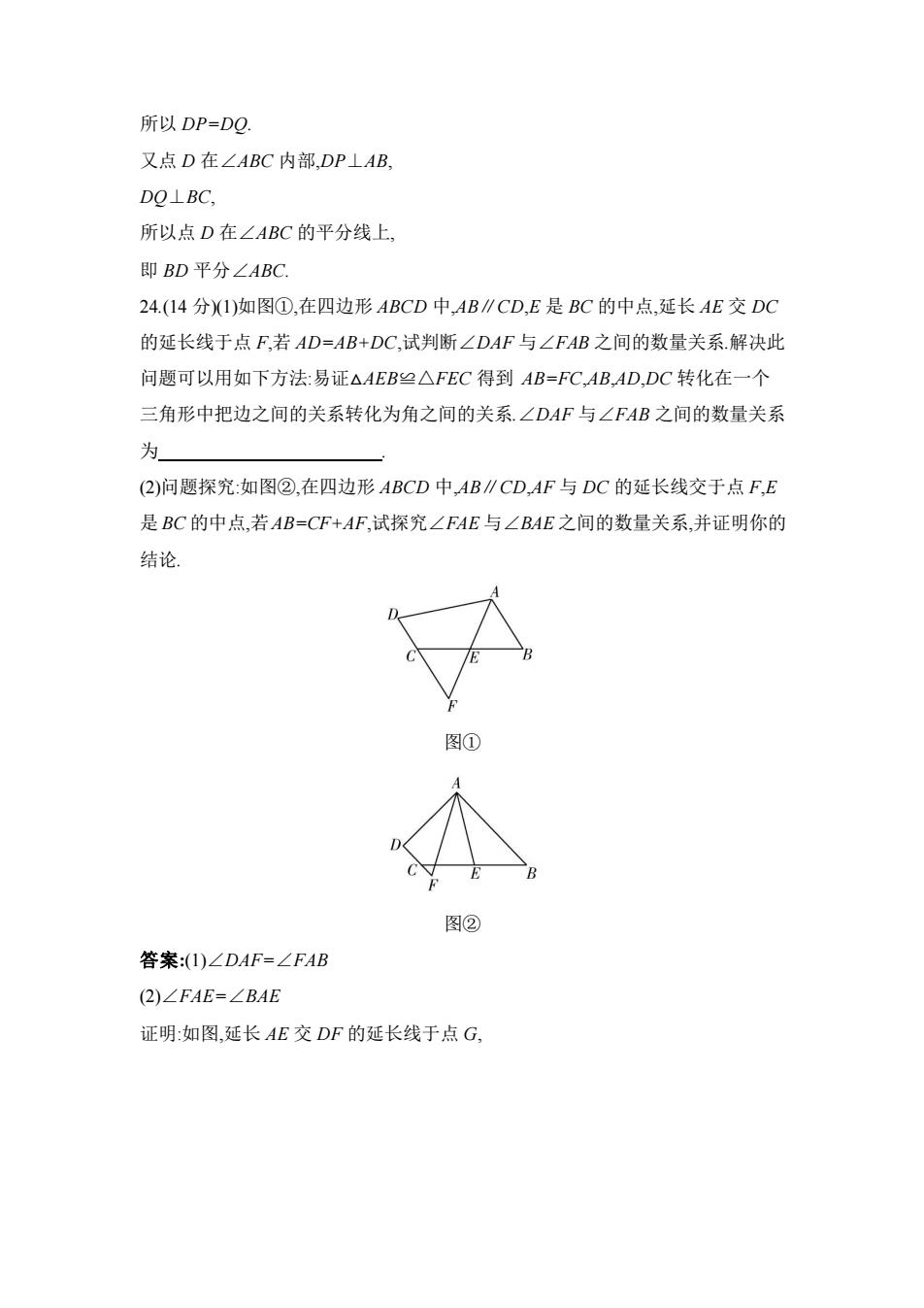
所以DP=DQ 又点D在∠ABC内部,DP⊥AB. DQ⊥BC, 所以点D在∠ABC的平分线上, 即BD平分∠ABC 24.(14分1)如图①,在四边形ABCD中,AB∥CD,E是BC的中点,延长AE交DC 的延长线于点F,若AD=AB+DC,试判断∠DAF与∠FAB之间的数量关系.解决此 问题可以用如下方法:易证△AEB≌△FEC得到AB=FC,AB,AD,DC转化在一个 三角形中把边之间的关系转化为角之间的关系.∠DAF与∠FAB之间的数量关系 为 (2)问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E 是BC的中点,若AB=CF+AF,试探究∠FAE与∠BAE之间的数量关系,并证明你的 结论 图① 图② 答案:(I)∠DAF=∠FAB (2)∠FAE=∠BAE 证明:如图,延长AE交DF的延长线于点G
所以 DP=DQ. 又点 D 在∠ABC 内部,DP⊥AB, DQ⊥BC, 所以点 D 在∠ABC 的平分线上, 即 BD 平分∠ABC. 24.(14 分)(1)如图①,在四边形 ABCD 中,AB∥CD,E 是 BC 的中点,延长 AE 交 DC 的延长线于点 F,若 AD=AB+DC,试判断∠DAF 与∠FAB 之间的数量关系.解决此 问题可以用如下方法:易证△AEB≌△FEC 得到 AB=FC,AB,AD,DC 转化在一个 三角形中把边之间的关系转化为角之间的关系.∠DAF 与∠FAB 之间的数量关系 为 . (2)问题探究:如图②,在四边形 ABCD 中,AB∥CD,AF 与 DC 的延长线交于点 F,E 是 BC 的中点,若AB=CF+AF,试探究∠FAE 与∠BAE 之间的数量关系,并证明你的 结论. 图① 图② 答案:(1)∠DAF=∠FAB (2)∠FAE=∠BAE 证明:如图,延长 AE 交 DF 的延长线于点 G

因为E是BC的中点, 所以CE=BE, 因为AB∥DC, 所以∠BAE=∠G 在△AEB和△GEC中, (LBAE=∠G, LAEB LGEC, BE CE, 所以△AEB≌△GEC(AAS) 所以AB=GC 因为AB=CF+AF, 所以GC=CF+AF 因为GC=CF+FG, 所以FA=FG 所以∠G=∠FAE: 所以∠FAE=∠BAE 25.(14分)八(1)班同学在数学活动课上,利用角尺平分一个角,设计了如下方案 (I)∠AOB是一个任意角,让角尺的直角顶点P介于射线OA,OB之间,移动角尺使 角尺两边相同的刻度分别与OA,OB交于点M,点N,即PM=PN,过角尺顶点P的射 线OP就是∠AOB的平分线 (IⅡ)如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,让角尺的直角顶点 P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN, 过角尺顶点P的射线OP就是∠AOB的平分线 (1)方案(I)、方案(Ⅱ)是否可行?若可行,请给出证明:若不可行,请说明理由 (2)在方案(I)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.这时此 方案是否可行?请说明理由
因为 E 是 BC 的中点, 所以 CE=BE. 因为 AB∥DC, 所以∠BAE=∠G. 在△AEB 和△GEC 中, { ∠𝐵𝐴𝐸 = ∠𝐺, ∠𝐴𝐸𝐵 = ∠𝐺𝐸𝐶, 𝐵𝐸 = 𝐶𝐸, 所以△AEB ≌△GEC(AAS). 所以 AB=GC. 因为 AB=CF+AF, 所以 GC=CF+AF. 因为 GC=CF+FG, 所以 FA=FG. 所以∠G=∠FAE. 所以∠FAE=∠BAE. 25.(14 分)八(1)班同学在数学活动课上,利用角尺平分一个角,设计了如下方案: (Ⅰ)∠AOB 是一个任意角,让角尺的直角顶点 P 介于射线 OA,OB 之间,移动角尺使 角尺两边相同的刻度分别与 OA,OB 交于点 M,点 N,即 PM=PN,过角尺顶点 P 的射 线 OP 就是∠AOB 的平分线. (Ⅱ)如图,∠AOB 是一个任意角,在边 OA,OB 上分别取 OM=ON,让角尺的直角顶点 P 介于射线 OA,OB 之间,移动角尺使角尺两边相同的刻度与 M,N 重合,即 PM=PN, 过角尺顶点 P 的射线 OP 就是∠AOB 的平分线. (1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请给出证明;若不可行,请说明理由. (2)在方案(Ⅰ)PM=PN 的情况下,继续移动角尺,同时使 PM⊥OA,PN⊥OB.这时此 方案是否可行?请说明理由

解:(I)方案(I)不可行,缺少证明三角形全等的条件.因为只有OP=OP,PM=PN,不 能判断△OPM≌△OPN,进而也无法判定OP就是∠AOB的平分线.方案(IⅡ)可行 证明方案(Ⅱ)如下: 在△OPM和△OPN中, (OM=ON, PM=PN, OPOP, 所以△OPM≌△OPN(SSS). 所以∠AOP=∠BOP, 即OP平分∠AOB. (2)当∠AOB是直角时,此方案可行 理由:因为PM⊥OA,PN⊥OB, 所以∠OMP=∠ONP=90°. 因为四边形ONPM的内角和为360°, ∠MPN=90°, 所以∠AOB=90 又PM⊥OA,PN⊥OB 且PM=PN, 所以OP为∠AOB的平分线(角的内部到角的两边距离相等的点在角的平分线上) 当∠AOB不为直角时,此方案不可行 理由:若∠AOB不为直角, 则不能找到同时使PMLOA,PN⊥OB成立的点P的位置
解:(1)方案(Ⅰ)不可行,缺少证明三角形全等的条件.因为只有 OP=OP,PM=PN,不 能判断△OPM ≌△OPN,进而也无法判定 OP 就是∠AOB 的平分线.方案(Ⅱ)可行. 证明方案(Ⅱ)如下: 在△OPM 和△OPN 中, { 𝑂𝑀 = 𝑂𝑁, 𝑃𝑀 = 𝑃𝑁, 𝑂𝑃 = 𝑂𝑃, 所以△OPM ≌△OPN (SSS). 所以∠AOP=∠BOP, 即 OP 平分∠AOB. (2)当∠AOB 是直角时,此方案可行. 理由:因为 PM⊥OA,PN⊥OB, 所以∠OMP=∠ONP=90°. 因为四边形 ONPM 的内角和为 360°, ∠MPN=90°, 所以∠AOB=90°. 又 PM⊥OA,PN⊥OB, 且 PM=PN, 所以OP为∠AOB的平分线(角的内部到角的两边距离相等的点在角的平分线上). 当∠AOB 不为直角时,此方案不可行. 理由:若∠AOB 不为直角, 则不能找到同时使 PM⊥OA,PN⊥OB 成立的点 P 的位置